Red black tree
Next to the last hashmap, we will talk about the operation of the red black tree.
Advantages: the red black tree is easy to find, and the time complexity is the height of the tree.
We should all know the basic principle of the red black tree. I'll write it again here:
- Each node on the tree is either black or red
- The root node is black
- Leaf nodes are black
- A red node. Both its children are black
- Any path from any node to its leaf node contains the same number of black nodes.
Come on, let's look at the formation and deletion, left-hand, right-hand and search of the red black tree.
Basic structure
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> { TreeNode<K,V> parent; // Parent of node TreeNode<K,V> left; // Left node of node TreeNode<K,V> right; // Right node of node TreeNode<K,V> prev; // The previous node (not the previous one in the tree) //As hashmap has said before, before changing from linked list to red black tree, it will first change to treenode < K, V > linked list, //Then convert it to a red black tree. prev here is the previous treenode < K, V > list here. boolean red; // Node color TreeNode(int hash, K key, V val, Node<K,V> next) { //The parent of the TreeNode's parent class is Node. super(hash, key, val, next); } }
Add node
When the length of the linked list is greater than or equal to 8, and the length of the table is greater than or equal to 64, the linked list will be converted to a red black tree.
The following method is called by treeifyBin method in hashmap.
final void treeify(Node<K,V>[] tab) { TreeNode<K,V> root = null; // Traversing TreeNode linked list for (TreeNode<K,V> x = this, next; x != null; x = next) { next = (TreeNode<K,V>)x.next; x.left = x.right = null; // Root node found if (root == null) { x.parent = null; x.red = false; root = x; } //Non root node else { K k = x.key; // Key of node int h = x.hash; // Node value Class<?> kc = null;// Type of key // Traverse from root for (TreeNode<K,V> p = root;;) { // There are only two results for dir, - 1 or 1. This is the result of comparing the hash values of the p node and the x node keys // P h is the hash value of the key of p; h is the hash value of the key of x // h > ph dir = 1; h < ph dir = -1； // dir determines whether x should be to the right or left of p. int dir, ph; K pk = p.key; if ((ph = p.hash) > h) dir = -1; else if (ph < h) dir = 1; else if ((kc == null && (kc = comparableClassFor(k)) == null) || (dir = compareComparables(kc, k, pk)) == 0) dir = tieBreakOrder(k, pk); // If you can't compare the hash values of the p and x keys, then use tiebreak order //This method compares the size of hashcode of their two keys. TreeNode<K,V> xp = p; //Only if there is no left or right node of p node, x will join in, otherwise, it will loop until p is the last node if ((p = (dir <= 0) ? p.left : p.right) == null) { x.parent = xp; if (dir <= 0) xp.left = x; else xp.right = x; root = balanceInsertion(root, x); // Add one node and balance the tree once break; } } } } // Put the root node first. moveRootToFront(tab, root); }
- Traverse the linked list, take node x, left and right nodes of the node are empty.
- Is root empty. root = x, the parent node of root is empty and the color is black.
- Root is not empty. Start from root to traverse the tree, take tree node P, and compare the hash size of the key with node x (p h is the hash value of the key of P, h is the hash value of the key of x)
- If H > pH, X should be on the right side of p.
- If the right node of p is empty, then x becomes the right node of p
- If the right node of p is not empty, the right node of p becomes p. Then compare.
- If h < ph, x should be to the left of p.
- If the left node of p is empty, then x becomes the left node of p.
- If the left node of p is not empty, the left node of p becomes p. Then compare.
- If H > pH, X should be on the right side of p.
Add a node balance tree once.
Equilibrium node
// Parameters are the root node and the added node. The added node may destroy the tree balance. After balancing, it is possible to change the root node of the tree, so return to the root node. static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root, TreeNode<K,V> x) { x.red = true; // xp is the parent node of x, xpp is the grandfather node of x, xppl is the left node of grandfather node, xppr is the right node of grandfather node. for (TreeNode<K,V> xp, xpp, xppl, xppr;;) { if ((xp = x.parent) == null) { // The parent node of X node is null, indicating that x is the root node, ending x.red = false; return x; } else if (!xp.red || (xpp = xp.parent) == null) // Parent node is not red or grandfather node does not exist, end return root; //If none of the above conditions are satisfied, then it means that x has a grandfather node, and the color of x and its parent node is red, //To balance, first of all, we need to see whether the parent node of x is the left node or the right node of the grandfather node, with different positions and different methods. if (xp == (xppl = xpp.left)) { if ((xppr = xpp.right) != null && xppr.red) { xppr.red = false; xp.red = false; xpp.red = true; x = xpp; } else { if (x == xp.right) { root = rotateLeft(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; } if (xp != null) { xp.red = false; if (xpp != null) { xpp.red = true; root = rotateRight(root, xpp); } } } } else { if (xppl != null && xppl.red) { xppl.red = false; xp.red = false; xpp.red = true; x = xpp; } else { if (x == xp.left) { root = rotateRight(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; } if (xp != null) { xp.red = false; if (xpp != null) { xpp.red = true; root = rotateLeft(root, xpp); } } } } } }
See the figure for the following situations:
- When we insert a new node, which causes this situation, we need to balance the nodes.
Dextral rotation
- xpp exists and the left node of xpp exists
- Assign the right node of xp to the left node of xpp. The right node of xp is larger than xp and smaller than xpp.
- The parent of xpp is assigned to the parent of xp
- The right node of xp is xpp.
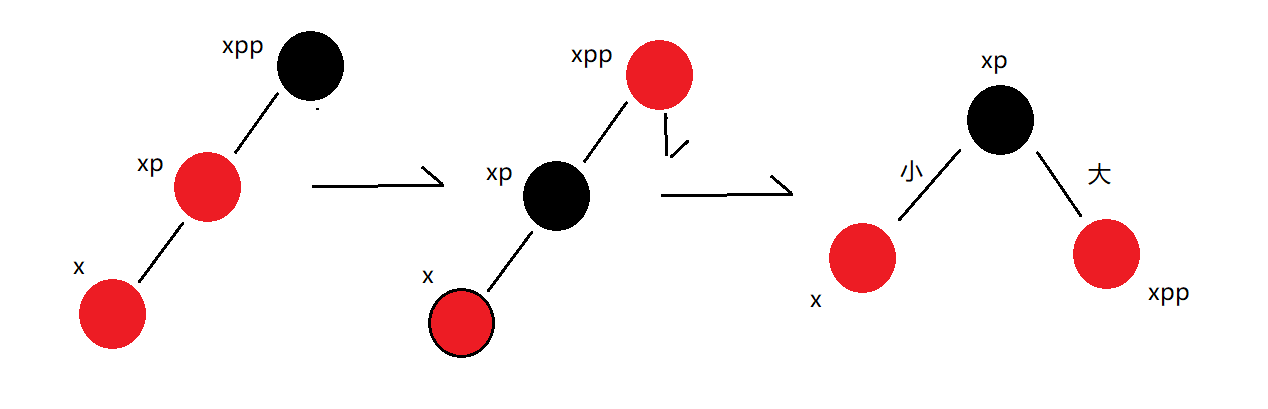2. Insert a node and balance the situation
Levo
- In this case, the last two nodes are rotated based on xp. Whether xp exists, and whether the right node of xp, xr exists
- The left node of xr is assigned to the right node of xp
- The parent of xp is assigned to the parent of xr
- The left node of xr is xp
It's not over yet, because it's not balanced, it's the same as the first situation, so the next step is the same as the first one.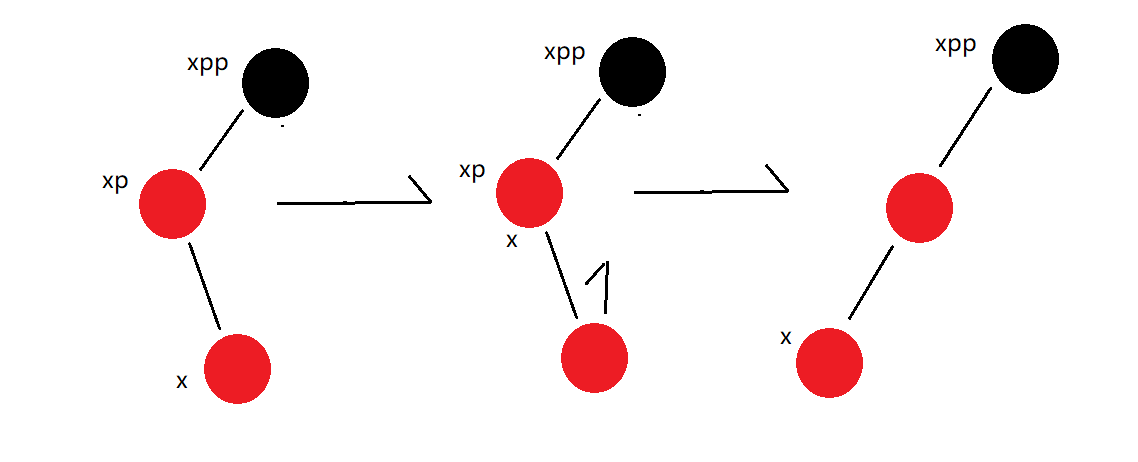
3. Another situation
This is to achieve the tree balance by changing the node color, which may affect other nodes, so in this case, we need to traverse to the root node to ensure that there are no two consecutive nodes that are red.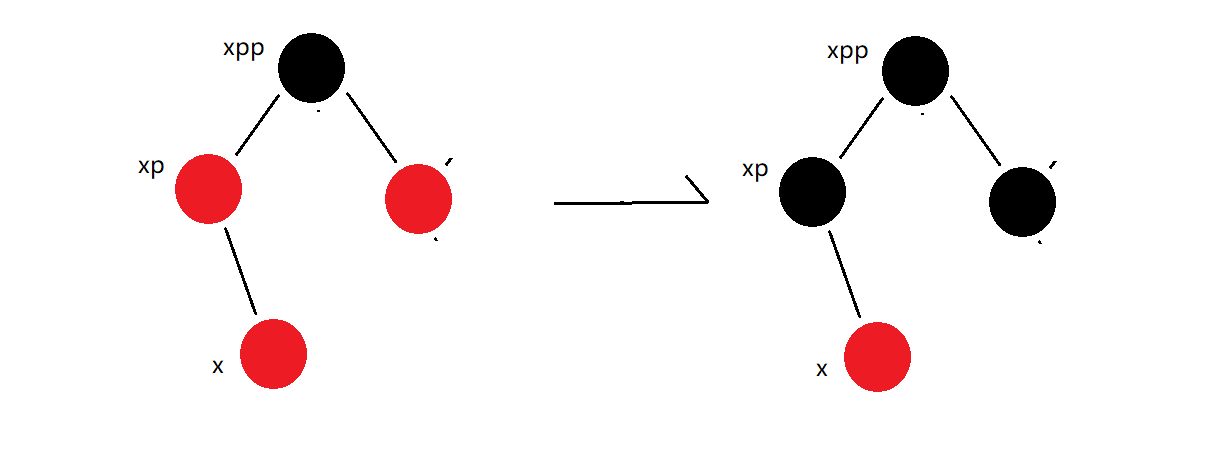
I only introduced the situation on the left, and the situation on the right is similar to this.
This is the case of adding a node.
Delete node
final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab, boolean movable) { int n; if (tab == null || (n = tab.length) == 0) return; int index = (n - 1) & hash; TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl; // Next is the next node to be deleted, prev is the previous node to be deleted TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev; // First, delete this node from the TreeNode list. if (pred == null) tab[index] = first = succ; else pred.next = succ; if (succ != null) succ.prev = pred; if (first == null) return; if (root.parent != null) root = root.root(); if (root == null || root.right == null || (rl = root.left) == null || rl.left == null) { // From red black tree to linked list tab[index] = first.untreeify(map); // too small return; } // Remove this node from the red black tree TreeNode<K,V> p = this, pl = left, pr = right, replacement; // p is the node to be deleted pl is the left node of p, pr is the right node of p. // When the left and right nodes of p are not null if (pl != null && pr != null) { TreeNode<K,V> s = pr, sl; while ((sl = s.left) != null) // find successor s = sl; boolean c = s.red; s.red = p.red; p.red = c; // swap colors TreeNode<K,V> sr = s.right; TreeNode<K,V> pp = p.parent; if (s == pr) { // p was s's direct parent p.parent = s; s.right = p; } else { TreeNode<K,V> sp = s.parent; if ((p.parent = sp) != null) { if (s == sp.left) sp.left = p; else sp.right = p; } if ((s.right = pr) != null) pr.parent = s; } p.left = null; if ((p.right = sr) != null) sr.parent = p; if ((s.left = pl) != null) pl.parent = s; if ((s.parent = pp) == null) root = s; else if (p == pp.left) pp.left = s; else pp.right = s; if (sr != null) replacement = sr; else replacement = p; } else if (pl != null) replacement = pl; else if (pr != null) replacement = pr; else replacement = p; if (replacement != p) { TreeNode<K,V> pp = replacement.parent = p.parent; if (pp == null) root = replacement; else if (p == pp.left) pp.left = replacement; else pp.right = replacement; p.left = p.right = p.parent = null; } TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement); if (replacement == p) { // detach TreeNode<K,V> pp = p.parent; p.parent = null; if (pp != null) { if (p == pp.left) pp.left = null; else if (p == pp.right) pp.right = null; } } if (movable) moveRootToFront(tab, r); }
Here I'll draw a picture for you to explain. It's quite clear. The red black tree in the figure below is explained as an example. p is the node to delete.
In short, to delete a p node, the operation here is to exchange the positions of P and s, and let s replace P.
Why s. Because the s node is just as big as the pl node and smaller than the pr node. So first we have to find the last left node on the left of pr.
We have a right node on s in this graph. What about this node. We give this node to the parent node of S, and let the right node of s become the left node of the parent node of S.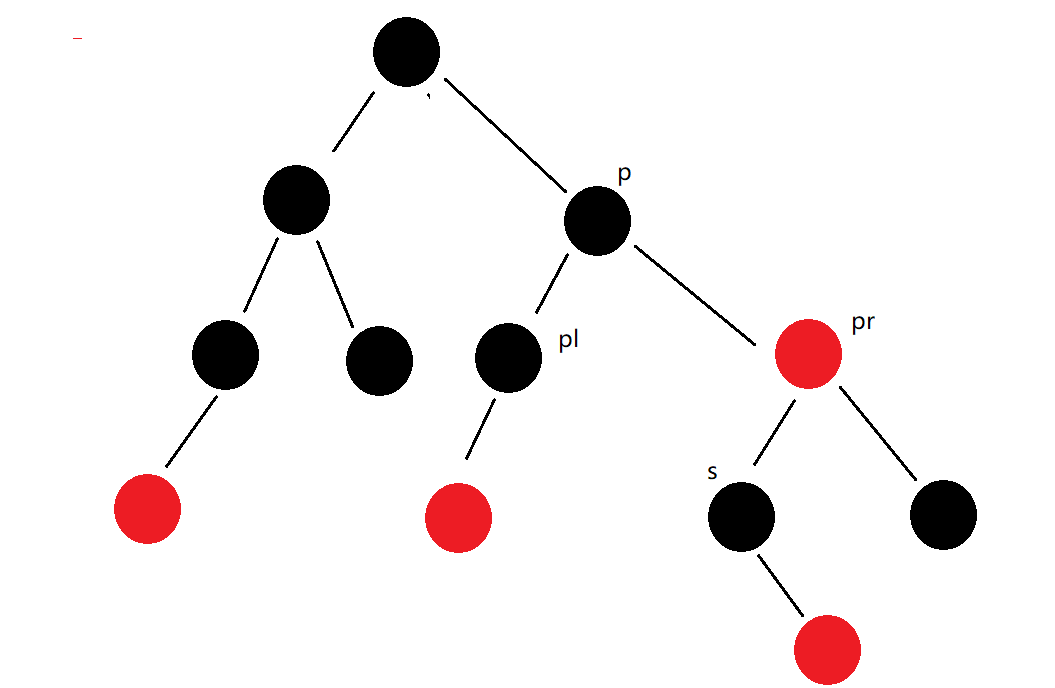
Look at the code again. There are several situations when deleting nodes on the tree
- The left and right nodes of the p node exist
- First, find the location of the s node,
- If s equals pr, then let the parent node of p become s, and the right node of s become p
- If s is not equal to pr, then the parent node of p node becomes the parent node SP of s node. That is, SP is now the father of p node. p becomes the left node of sp.
- pr becomes the right node of s node
- Assign the right node of s to the right node of p
- Assign the left node of p to the left node of s
- Assign the parent of p to the parent of s
- First, find the location of the s node,
- There is only one left and right node of p node
- p node has no left and right nodes
- According to the replacement, judge whether to delete the p node directly or whether there are other operations.
Of course, deleting may also destroy the tree balance, so balance,
I read about the self balance of the red black tree after deleting nodes, but I didn't understand it. I will add it when I understand it.
