catalogue

Two universal templates

1. Subset

2. Subset II

3. Combination

4. Combination sum

5. Combined sum II

6. Full arrangement

7. Full arrangement II

8. Full arrangement of strings

9. Letters are arranged in full case

Two universal templates

• Method 1: the relative order remains unchanged

Go from left to right start Number of control layers

vector<vector<int>> vv;
vector<int> v;

dfs(vector<int>& nums, int start)
{
    if(start == nums.size())
    {
        vv.push_back(v);
        return;
    }
    v.push_back(nums[start]);
    dfs(nums, start+1);
    v.pop_back();
    dfs(nums, start+1);
}

• Method 2: the relative order remains unchanged (the problem of changing the relative order can be solved with vector < bool > visit)

start Number of control layers  (According to the requirements of the topic , Use the required conditions to control when to return)

vector<vector<int>> vv;
vector<int> v;

dfs(vector<int>& nums, int start)
{
    if(start == nums.size())
    {
        vv.push_back(v);
        return;
    }
    for (int i = start; i < nums.size(); ++i)  // This is the case where each number can only be taken once
    {
        v.push_back(nums[i]);
        dfs(nums, i+1);
        v.pop_back();
    }
}

After the above two templates are understood, we can start to brush the questions (if you don't understand, you can draw a recursive graph to understand)

1.subset

Give you an integer array {nums. The elements in the array are different from each other. Returns all possible subsets (power sets) of the array.

The solution set cannot contain duplicate subsets. You can return the solution set in any order.

Example 1:

Input: num = [1,2,3]
Output: [[], [1], [2], [1,2], [3], [1,3], [2,3], [1,2,3]]

Method 1: perfect solution

class Solution {
public:
	vector<int> v;                          // Single subset
	vector<vector<int>> vv;                // Subset set

	void dfs(int cur, vector<int>& nums) {  // cur: array position of the current search
		if (cur == nums.size()) {           // Recursive lower bound
			vv.push_back(v);               // Save the results of this trip
			return;
		}
		v.push_back(nums[cur]);             // Add current element
		dfs(cur + 1, nums);                 // Enter the next state
		v.pop_back();                       // To go back to a state in which the current element is not added
		dfs(cur + 1, nums);                 // Enter the next state
	}

	vector<vector<int>> subsets(vector<int>& nums) {
		dfs(0, nums);
		return vv;
	}
};

Now briefly analyze the code recursion process:

V. depth first traversal -- [] 1] [1,2] [1,2,3] cur value becomes 3 vv push_ back(v) return 

Cur value fallback to 2 # v.pop -- [1,2] recurse to the next level cur = 3 [1,2] into vv return

Cur  value fallback to 2  function end cur fallback to 1 v.pop -- [1] recursive next layer cur = 2

                        v.push_back(nums[2]) -- [1,3] cur = 3  vv.push_back(v) return ......

If you have a little trouble, don't simulate. The later process is exactly the same. The final result is as follows

[1,2,3] [1,2] [1,3] [1] [2,3] [2] [3] [] 

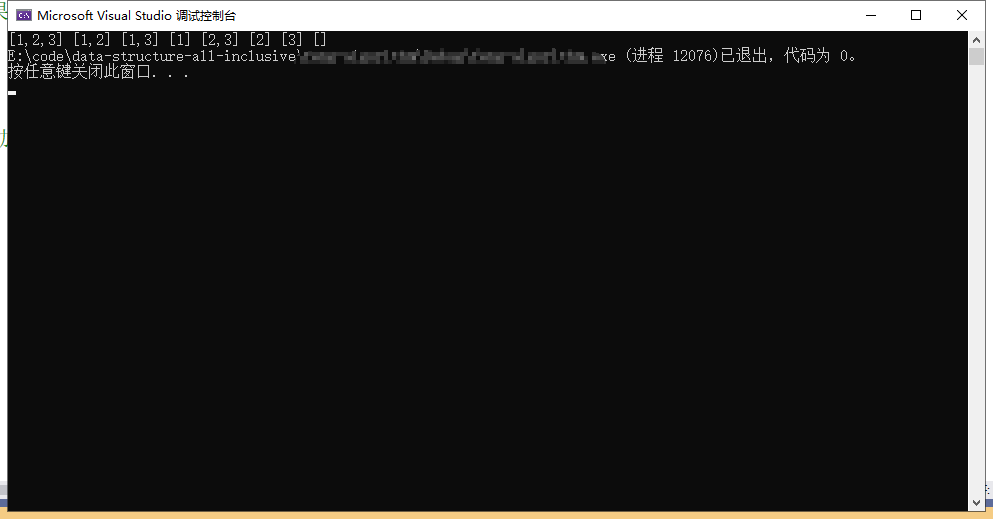
Can method 2 be used here? Absolutely. We used i = start to control it, and it will not happen [2,1,3]

class Subsets
{
public:

	vector<vector<int>> vv;
	vector<int> v;

	void dfs(vector<int>& nums, int start)
	{
		vv.push_back(v);    // Rag collectors are welcome
		for (int i = start; i < nums.size(); ++i)
		{
			v.push_back(nums[i]);
			dfs(nums, i + 1);
			v.pop_back();
		}
	}

	vector<vector<int>> subsets(vector<int>& nums) {
		dfs(nums, 0);
		return vv;
	}
};

In what order did v ？ enter vv ？?

[] [1] [1,2] [1,2,3] start = 3 now directly return start=2 v.pop [1,2] i = 2 end i++ i = 3 return start=2 end of this layer start = 1 pop v = [1] i = 1 end i = 2 push [1,3] start = 3 (i+1 = 3)

[] [1] [1,2] [1,2,3] [1,3] [2] [2,3] [3] brainstorming. The sequence should be as follows. Procedure inspection:

 

 

2.Subset II

Give you an integer array nums, which may contain duplicate elements. Please return all possible subsets (power sets) of the array.

The solution set cannot contain duplicate subsets. Subsets of the returned solution set can be arranged in any order.

Input: num = [1,2,2]
Output: [[], [1], [1,2], [1,2,2], [2], [2,2]]

• Sort arrays
• De duplication (vector < bool > VIS)

Determine which template to use - for} circular version is easier to control

i > 0 && nums[i] == nums[i - 1] && visit[i-1]==false  

The key control steps are 1,2,2 ， if the first 2 ， doesn't go in, the second 2 doesn't need to go in, otherwise it will be repeated

class Solution {

public:
    vector<int> v;
    vector<vector<int>> vv;
    vector<bool> visit;

    void dfs(vector<int>& nums, int start)
    {
        vv.push_back(v);
        for (int i = start; i < nums.size(); ++i)
        {
            if (i > 0 && nums[i] == nums[i - 1] && visit[i-1]==false)
                continue;
            v.push_back(nums[i]);
            visit[i] = true;
            dfs(nums, i + 1);
            v.pop_back();
            visit[i] = false;
        }
    }
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        visit.resize(nums.size());
        dfs(nums, 0);
        return vv;
    }

3.combination

Given two integers ， n ， and ， k, returns the combination of all possible ， k ， numbers in the range [1, n].

You can return answers in {any order.

Input: n = 4, k = 2
 Output:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

It's very simple. One or two methods are OK

class Solution{
public:
	vector<vector<int>> vv;
	vector<int> v;

	void dfs(int start, int n, int k)
	{
		if (v.size() == k)
		{
			vv.push_back(v);
			return;
		}
		for (int i = start; i < n; ++i)
		{
			v.push_back(i + 1);
			dfs(i + 1, n, k);
			v.pop_back();
		}
	}

	vector<vector<int>> combine(int n, int k) {

		dfs(0, n, k);
		return vv;
	}
};

class Solution2 {
public:
	vector<vector<int>> vv;
	vector<int> v;

	void dfs(int start, int n, int k)
	{
		if (v.size() == k)
		{
			vv.push_back(v);
			return;
		}
		if (start == n + 1)return;
		v.push_back(start);
		dfs(start + 1, n, k);
		v.pop_back();
		dfs(start + 1, n, k);
	}

	vector<vector<int>> combine2(int n, int k) {

		dfs(1, n, k);
		return vv;
	}
};

4.Combined sum

Give you an array of integers with no duplicate elements, @ candidates, and a target integer, @ target. Find out all the different combinations of numbers and target numbers in ， candidates ， and return them in the form of a list. You can return these combinations in any order.

The same number in candidates can be selected repeatedly without restriction. If the selected number of at least one number is different, the two combinations are different.  

For a given input, ensure that the number of different combinations with sum target is less than 150.

Input: candidates = [2,3,6,7], target = 7
Output: [[2,2,3], [7]]
Explanation:
2 and 3 can form a set of candidates, 2 + 2 + 3 = 7. Note 2 can be used multiple times.
7 is also a candidate, 7 = 7.
There are only two combinations

• You can use start unlimited times. Start is no longer used to control the termination condition. sum is used to control the termination condition
• for loop  start with i = 0  ensure that each position can be taken multiple times

However, there is a problem in using this method. There is no way to duplicate it - - - [2,2,3] [2,3,2] [3,2,2] will be push ed in

Use method I

The following is the wrong version!!! (there are also solutions. Add start i=start to control it to find the number to the right)

calss Solution{
public:
	vector<vector<int>> vv;
	vector<int> v;


	void dfs(vector<int>& candidates, int target, int sum)
	{
		if (sum == target)
		{
			vv.push_back(v);
			return;
		}
		else if (sum > target)return;
		for (int i = 0; i < candidates.size(); ++i)
		{
			v.push_back(candidates[i]);
			dfs(candidates, target, sum + candidates[i]);
			v.pop_back();
		}
		//How to control it to only look to the right / / the non for circular version can solve this problem
	}
	vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
		int sum = 0;
		//sort(candidates.begin(),candidates.end());
		dfs(candidates, target, sum);
		return vv;
	}
};

Correct version!!! start must * * enter the factory * *

start does not control the number of recursion layers. It is used to judge whether it is out of bounds

class CombinationSum {
public:
	vector<vector<int>> vv;
	vector<int> v;


	void dfs(vector<int>& candidates, int target, int sum, int start)
	{
		if (sum == target)
		{
			vv.push_back(v);
			return;
		}
		else if (sum > target || start==candidates.size())
			return;
		
		v.push_back(candidates[start]);
		dfs(candidates, target, sum + candidates[start], start);//Recursive itself
		v.pop_back();
		dfs(candidates, target, sum, start + 1);//Recursive next bit
	}

	vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
		int sum = 0;
		dfs(candidates, target, sum, 0);
		return vv;
	}
};

5.Combined sum II

Give you a set of candidate elements, candidates ， and a target number ， and find all combinations in ， candidates ， that can make the sum of numbers ， target.

Each element in candidates can only be used once in each combination.

• Each number can only be used once + to contain duplicate arrays

Old rule: vis + two judgments to solve this problem

class Solution {
public:
	vector<vector<int>> vv;
	vector<int> v;
	vector<bool> vis;


	void dfs(vector<int>& candidates,int target, int sum, int start)
	{
		//A number can only be used once. It's easy to say double recursion - > combination | for loop - > arrangement
		if (sum == target)
		{
			vv.push_back(v);
			return;
		}
		if (sum > target || start >= candidates.size())return;
		if(start>0 && candidates[start]==candidates[start-1] && vis[start-1]==false)//[1,1,6] [1,2,5] [1,7] [2,6]
		{ 
			dfs(candidates, target, sum, start + 1); 
		}
		else
		{
			vis[start] = true;
			v.push_back(candidates[start]);
			dfs(candidates, target, sum + candidates[start], start + 1);
			vis[start] = false;
			v.pop_back();
			dfs(candidates, target, sum, start + 1);
		}
	}

    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
		sort(candidates.begin(), candidates.end());
		vis.resize(candidates.size());
		dfs(candidates, target, 0, 0);
		return vv;
	}
};

6.Full arrangement

Given an array of {nums without duplicate numbers, all possible permutations of} are returned. You can} return answers in any order.

Input: candidates = [10,1,2,7,6,1,5], target = 8,
Output:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

The official gives the classic swap method, but we only use the above two templates, so continue to use the above method to solve this problem

• Start from zero every time to detect which number has not been accessed, mark the accessed flag true, and mark back false when tracing back

class Solution {
	vector<vector<int>> vv;
	vector<int> v;
	vector<bool> vis;
public:
	void dfs(vector<int>& nums, int start)
	{
		if (start == nums.size())
		{
			vv.push_back(v);
			return;
		}
		for (int i = 0; i < nums.size(); ++i)
		{
			if (vis[i] == true)continue;
			v.push_back(nums[i]);
			vis[i] = true;
			dfs(nums, start+1);
			v.pop_back();
			vis[i] = false;
		}
	}

	vector<vector<int>> permute(vector<int>& nums) {
		vis.resize(nums.size());
		dfs(nums, 0);
		return vv;
	}
};

Official solution:

class Solution {
public:
    void dfs(vector<vector<int>>& vv, vector<int>& nums, int first, int len)
    {
        if(first == len)
        {
            vv.push_back(nums);
            return;
        }
        for(int i=first; i<len; ++i)
        {
            swap(nums[first], nums[i]);
            dfs(vv,nums,first+1,len);
            swap(nums[first], nums[i]);
        }
    }

    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> vv;
        dfs(vv, nums, 0, nums.size());
        return vv;
    }
};

7.Full arrangement II

Given a sequence of {nums that can contain repeated numbers,} returns all non repeated full permutations in any order.

• Sort first, and then set conditions to remove duplicates
• vis[i] == true || (i>0 && nums[i]==nums[i-1] && vis[i-1]==false

class Solution {
public:
	vector<vector<int>> vv;
	vector<int> v;
	vector<bool> vis;
	void dfs(vector<int>& nums, int start)
	{
		if (start == nums.size())
		{
			vv.push_back(v);
			return;
		}
		for (int i = 0; i < nums.size(); ++i)
		{
			if (vis[i] == true || (i>0 && nums[i]==nums[i-1] && vis[i-1]==false))continue;
			v.push_back(nums[i]);
			vis[i] = true;
			dfs(nums, start + 1);
			v.pop_back();
			vis[i] = false;
		}
	}

	vector<vector<int>> permuteUnique(vector<int>& nums) {
		vis.resize(nums.size());
		sort(nums.begin(), nums.end());
		dfs(nums, 0);
		return vv;
	}
};

8.Full arrangement of strings

As like as two peas, the method of removing weights is not in the same way.

In addition, the ontology can be optimized, and the string recursion directly:

Before optimization		str.append(1,s[i]); 
			vis[i] = true;
			dfs(s, start + 1);
			str = str.substr(0,str.length()-1);


After optimization      dfs(s+s[i], start + 1);
In order to forcibly match the template,It looks like it

class Solution {
public:
	vector<string> vs;
	vector<bool> vis;
	string str;
	void dfs(string& s, int start)
	{
		if (start == s.length())
		{
			vs.push_back(str);
			return;
		}
		for (int i = 0; i < s.length(); ++i)
		{
			if (vis[i] == true || (i>0 && s[i]==s[i-1]&&vis[i-1]==false))continue;
			str.append(1,s[i]);  // There is no way to overload append (char). Only the fill function append(n,char) can be used
			vis[i] = true;
			dfs(s, start + 1);
			//str.erase(str.length()-1,string::npos);// The first defaults to 0 and the second defaults to - 1 npos
			str = str.substr(0,str.length()-1);
			vis[i] = false;

		}
	}
	vector<string> permutation(string s) {
		vis.resize(s.length());
		sort(s.begin(), s.end());
		dfs(s, 0);
		return vs;
	}
};

9.Letters are arranged in full case

Given a string S, we can get a new string by converting each letter in string S to case. Returns a collection of all possible strings.

After the above training, I believe this problem is very easy

class Solution {
public:
	vector<string> vs;
	void dfs(string& s, int start)
	{
		if (start == s.length())
		{
			vs.push_back(s);
			return;
		}
		if (isalpha(s[start]))
		{
			//Love and don't love algorithm
			s[start] = toupper(s[start]);
			dfs(s, start + 1);
			
			s[start] = tolower(s[start]);
			dfs(s, start + 1);
		}
		else
			dfs(s, start + 1);
	}

	vector<string> letterCasePermutation(string s) {
		dfs(s, 0);
		return vs;
	}
};

Let's stop here first. We'll sort out dynamic programming, greedy algorithm and search algorithm when we have time

The search algorithm is still very interesting

                                                                                                                        2022/1/6