1, Color model and conversion
1.1 RGB color model
RGB color space model: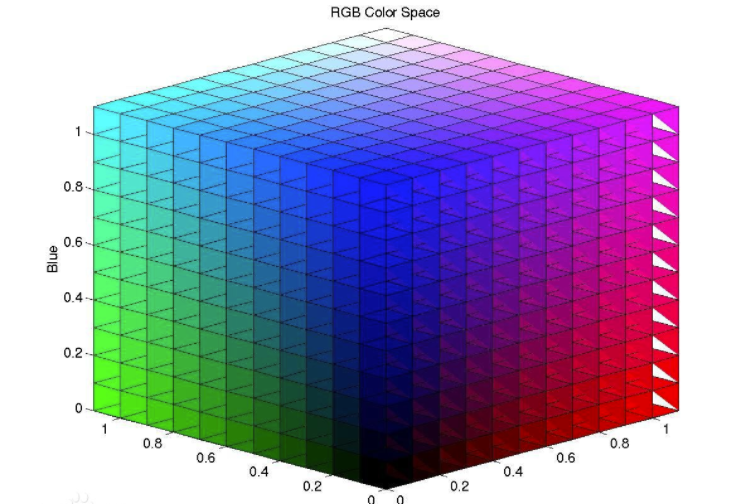
The model is named by using the English initials of three colors, namely red, green and blue. In the RGB model, all colors are the three colors. Through the mixing model of different proportions, if the three colors are zero, they are represented as black, and if the components of the three colors are the same and are the maximum, they are represented as white. On this basis, the fourth channel is added as RGBA model. The fourth channel represents the transparency of color. When there is no transparency requirement, RGBA model will degenerate into RGB model.
1.2YUV color model
YUV model is the color coding method used in TV signal system. These three variables represent the brightness (Y) of pixels, the difference between red component and brightness signal (U), and the difference between blue and brightness (V). This color model is mainly used for video and image transmission. The conversion relationship between RGB model and YUV model is as follows:

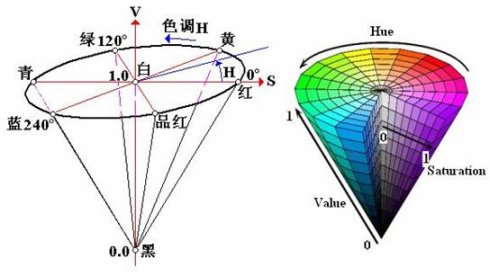
1.3 HSV color model
HSV is a representation of points in RGB color space in an inverted cone. HSV is hue, saturation and value, also known as HSB(B is Brightness). Hue is the basic attribute of color, which is commonly referred to as the name of color, such as red, yellow, etc. saturation (S) It refers to the purity of color. The higher the color is, the purer the color is, and the lower the color is, it will gradually turn gray, taking the value of 0-100%. The lightness (V) is 0-max (the value range of HSV in the computer is related to the length of storage) HSV color space can be described by a cone space model. At the apex of the cone, V=0, H and S are undefined, representing black. At the center of the top surface of the cone, V=max, S=0, H is undefined, representing white.
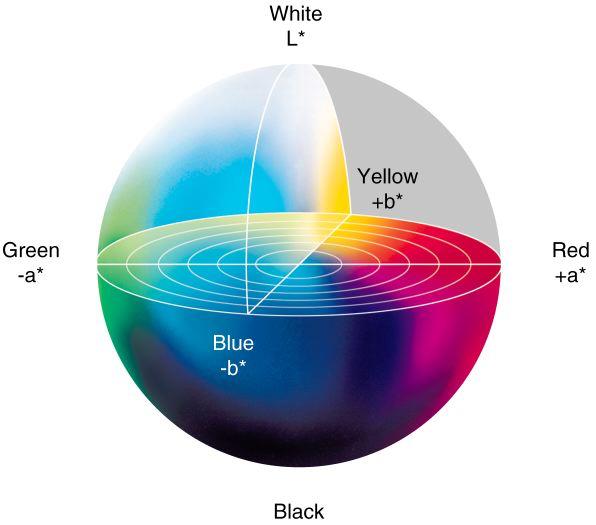
1.4Lab color model
Lab color model makes up for the deficiency of RGB color model. It is a color model independent of equipment and basic and physiological characteristics. In the model, L represents brightness, a and b are two color channels, and the value range of both is - 128 ~ 127. The value of channel a is from small to large, and the corresponding color changes from green to red, and the value of channel b is from small to large, and the corresponding color changes from blue to red Yellow.
1.5GRAY color model
GRAY model is not a color model, but a GRAY image. GRAY images have the advantages of the same size, the same yaso format, small capacity, easy acquisition, easy transmission, etc. commonly used methods of transforming RGB models into GRAY images are as follows:
GRAY = 0.3R+ 0.59G+ 0.11B
1.6 conversion between different color models
OpenCV provides the cvtColor() function for conversion.
void cv::cvtColor(InputArray src,
OutputArray dst,
int code,
int dstCn = 0
)src: the original image of the color model to be converted.
dst: the target image after converting the color model.
code: symbol of color space conversion.
dstCn: the number of channels in the target image.
If an alpha channel (the fourth channel in the RGB model, representing transparency) is added during the conversion, its value will be set to the maximum value of the corresponding channel range: CV_8U is 255, CV_16U is 65535, and CV_32F is 1.
| Flag parameters | Abbreviation | effect |
| COLOR_BGR2BGRA | 0 | Add alpha channel to RGB image |
| COLOR_BGR2RGB | 4 | Color image channel color order change |
| COLOR_BGR2GRAY | 10 | Convert color image into gray image |
| COLOR_GRAY2BGR | 8 | Convert gray image to color image (pseudo color) |
| COLOR_BGR2YUV | 82 | Convert RGB color model to YUV color model |
| COLOR_YUV2BGR | 84 | Convert YUV color model to RGB color model |
| COLOR_BGR2HSV | 40 | Convert RGB color model to HSV color model |
| COLOR_HSV2BGR | 54 | Convert HSV color model to RGB color model |
| COLOR_BGR2Lab | 44 | Convert BGR color model to Lab color model |
| COLOR_Lab2BGR | 56 | Convert Lab color model to RGB color model |
Code example:
#include<opencv2/opencv.hpp>
#include<iostream>
#include<vector>
using namespace std;
using namespace cv;
int main()
{
Mat img = imread("lena.png");
if (img.empty())
{
cout << "Please check whether the input image data is correct" << endl;
return -1;
}
Mat gray, HSV, YUV, Lab;
cvtColor(img, HSV, COLOR_BGR2HSV);
cvtColor(img, YUV, COLOR_BGR2YUV);
cvtColor(img, Lab, COLOR_BGR2Lab);
cvtColor(img, gray, COLOR_BGR2GRAY);
imshow("Original drawing", img);
imshow("HSV", HSV);
imshow("YUV", YUV);
imshow("Lab", Lab);
imshow("gray", gray);
waitKey(0);
return 0;
}2, Multichannel separation function and merging
2.1 multi channel separation function (split)
There are two overloaded prototypes for the multi-channel separation function split() in OpenCV.
void cv::split(const Mat &src,
Mat *mvbegin
)
void cv::split(InputArray m,
OutArray mv
)src: multichannel image with separation.
mvbegin: the separated single channel image is in the form of an array. The size of the array needs to be the same as the number of channels of the image.
m: Multi channel image with separation.
mv: single channel image after separation, in vector form.
Although the types of input parameters of the two function prototypes are different, the principle of channel separation is the same, which can be expressed by the following formula:
mv[c](I) = src(I)
2.2 multi channel merge function ()
OpenCV also has two overload prototypes for the multi-channel separation merge function merge().
void cv::merge(const Mat &mv,
size_t cout,
OutputArray dst
)
void cv::merge(InputArrayOfArrays mv,
OutputArray dst
)MV (the first overloaded prototype parameter): an array of images to be merged, where each image must have the same size and data type.
cout: the length of the input image array, which must be greater than 0.
MV (second overloaded prototype parameter): the image vector to be merged, where each image must have the same size and data type.
dst: the combined output image has the same size and data type as mv[0], and the number of channels is equal to the sum of the number of channels of all input images.
2.3 image multi-channel separation and merging routine
#include<opencv2/opencv.hpp>
#include<iostream>
#include<vector>
using namespace std;
using namespace cv;
int main()
{
Mat img = imread("C:\\Users\\Wang Yi\\Pictures\\f9afe18da2fb1fa2ff72c4d8b29fe6a (2).png");
if (img.empty())
{
cout << "Please check whether the input image data is correct" << endl;
return -1;
}
Mat HSV;
cvtColor(img, HSV, COLOR_BGR2HSV);
Mat imgs0, imgs1, imgs2; //Used to store the results of array types
Mat imgv0, imgv1, imgv2; //Used to store the results of vector type
Mat result0, result1, result2; //Results of multi-channel merging
//Multi channel separation and merging of input array parameters 0
Mat imgs[3];
split(img, imgs);
imgs0 = imgs[0];
imgs1 = imgs[1];
imgs2 = imgs[2];
imshow("RGB-B passageway", imgs0);
imshow("RGB-G passageway", imgs1);
imshow("RGB-R passageway", imgs2);
imgs[2] = img; //Make the number of image channels in the array inconsistent
merge(imgs, 3, result0); //Merge image
//Imshow ("result0", result0); imshow displays up to 4 channels, so the results can be viewed in Image Watch
Mat zero = cv::Mat::zeros(img.rows, img.cols, CV_8UC1);
imgs[0] = zero;
imgs[2] = zero;
merge(imgs , 3, result1);
imshow("result1", result1);
//Multi channel separation and merging of input vector parameters
vector<Mat> imgv;
split(HSV, imgv);
imgv0 = imgv.at(0);
imgv1 = imgv.at(1);
imgv2 = imgv.at(2);
imshow("HSV-H passageway", imgv0);
imshow("HSV-S passageway", imgv1);
imshow("HSV-V passageway", imgv2);
imgv.push_back(HSV); //Make the number of image channels in the vector inconsistent
merge(imgv, result2);
//Imshow ("result2", result2); imshow displays up to 4 channels, so the results are viewed in Image Watch
waitKey(0);
return 0;
}