1, Gradient processing of image
1. Sobel operator
Gradient can be calculated according to the x direction or y direction. In fact, it depends on the difference and change of pixel points, such as the junction of black-and-white objects. The difference of pixel value change is very large.
The function used for gradient calculation is called Sobel operator, which can be divided into horizontal gradient and vertical gradient.
Simply put, Sobel operator is a special convolution kernel, which can be used for image edge detection. Customize a Sobel operator in horizontal and vertical directions:

# Horizontal sobel operator
Sobel_x = np.array([[-1, 0, 1], 
                    [-2, 0, 2], 
                    [-1, 0, 1]])
# sobel operator in vertical direction
Sobel_y = np.array([[-1, -2, -1], 
                    [0, 0, 0], 
                    [1, 2, 1]])

It can be seen that when using sobel operator for convolution calculation, it is to add and subtract a circle of pixels in the middle pixel.
If the convolution operation is performed on pixels located in the same color, the operation result will be equal to 0, because the left and right values are the same.
Functions in opencv:

dst = cv.Sobel(src, ddepth, dx, dy, ksize)

ddepth: indicates the depth of the incoming image (number of color channels)
src: incoming image
dx and dy represent horizontal and vertical directions, respectively
ksize: indicates the size of sobel operator
cv.CV_64F: indicates that the operation results are stored in a larger storage mode, because negative numbers may occur
The code implements sobel operator:

def f_sobel():
    img = cv.imread("car_red.jpg", cv.IMREAD_GRAYSCALE)
    # Horizontal sobel operator
    Sobel_x = np.array([[-1, 0, 1],
                        [-2, 0, 2],
                        [-1, 0, 1]])
    # sobel operator in vertical direction
    Sobel_y = np.array([[-1, 0, -2],
                        [0, 0, 0],
                        [1, 0, 2]])
    dst = cv.Sobel(img, cv.CV_64F, dx=1, dy=0, ksize=3)
    cv.imshow("zero", dst)
    cv.waitKey(0)
    cv.destroyAllWindows()

The operation results are shown in the figure below:

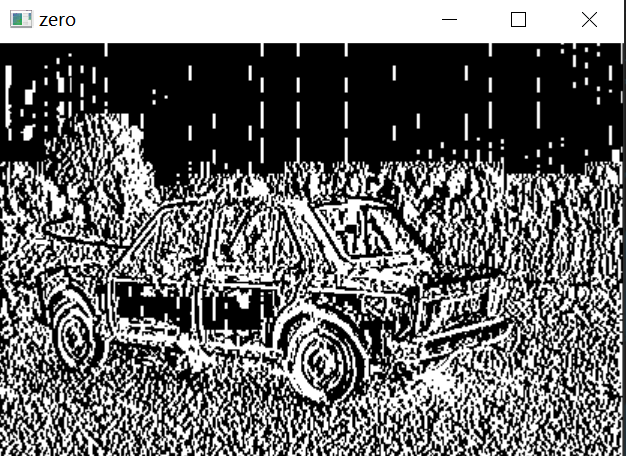
The result is not ideal. This is because the result of subtracting the left value from the right value is not always positive. Sometimes it is negative. opencv will automatically truncate the negative number and take 0. Therefore, it is necessary to change the negative number to a positive number at this time.

def f_sobel():
    img = cv.imread("car_red.jpg", cv.IMREAD_GRAYSCALE)
    # Horizontal sobel operator
    Sobel_x = np.array([[-1, 0, 1],
                        [-2, 0, 2],
                        [-1, 0, 1]])
    # sobel operator in vertical direction
    Sobel_y = np.array([[-1, 0, -2],
                        [0, 0, 0],
                        [1, 0, 2]])
    dst = cv.Sobel(img, cv.CV_64F, 1, 0, ksize=3)
    # This code will take the positive and negative absolute values
    dst = cv.convertScaleAbs(dst)
    cv.imshow("zero", dst)
    cv.waitKey(0)
    cv.destroyAllWindows()

The boundary is clear:

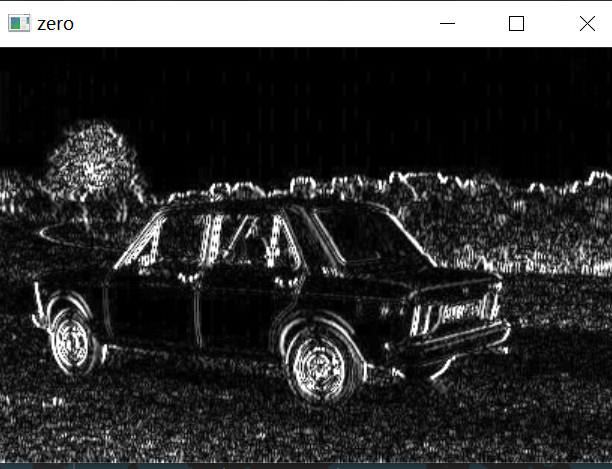
At the same time, the results obtained by using the horizontal or vertical direction are also different. Therefore, Sobel operator can be calculated for both horizontal and vertical directions, and then the two gradient images can be added to obtain a complete contour image.
code:

def f_sobel():
    img = cv.imread("car_red.jpg", cv.IMREAD_GRAYSCALE)
    # Horizontal sobel operator
    Sobel_x = np.array([[-1, 0, 1],
                        [-2, 0, 2],
                        [-1, 0, 1]])
    # sobel operator in vertical direction
    Sobel_y = np.array([[-1, 0, -2],
                        [0, 0, 0],
                        [1, 0, 2]])
    dst_x = cv.Sobel(img, cv.CV_64F, 1, 0, ksize=3)
    dst_y = cv.Sobel(img, cv.CV_64F, 0, 1, ksize=3)
    dst_y = cv.convertScaleAbs(dst_y)
    dst_x = cv.convertScaleAbs(dst_x)
    dst = cv.addWeighted(dst_x, 0.5, dst_y, 0.5, 0)
    cv.imshow("zero", dst)
    cv.waitKey(0)
    cv.destroyAllWindows()

result:

Scharr operator: compared with Sobel operator, the value is larger and more sensitive to the difference of results.

laplacian operator: more sensitive to noise points

# Horizontal Scharr operator
Scharr = np.array([[-3, 0, 3],
                   [-10, 0, 10],
                   [-3, 0, 3]])
# laplacian operator 
laplacian = np.array([[0, 1, 0],
                     [1, -4, 1],
                     [0, 1, 0]]) 

Function body:

# Parameters are similar to Sobel operators
cv2.Scharr(src, dx, dy....)
# Laplacian does not distinguish between X and Y directions. So there are no dx, dy parameters
cv2.Laplacian(src...)