Order statistics

After the array with length n is sorted in ascending order, the number at position i is the smallest quantity i of the array, which is called the ith order statistic

The minimum value of the array is the first order statistic, the maximum value is the nth order statistic, and the median (also known as the lower median) is the ⌊ (n+1)/2 ⌋ order statistic

⌊ n ⌋ means rounding down n and ⌈ n ⌉ means rounding up n

Maximum and minimum

If you want to find the maximum or minimum of N numbers, you only need to make (n-1) comparisons

int min = a[0];
for(int i=1;i<n;i++){
    if(a[i] > min)
        min = a[i];
}

Obviously, this is the optimal algorithm. We call it "traversal search", because the algorithm simply traverses the entire array to find the maximum or minimum value. It requires a total of (n-1) comparisons, that is, S(n)=n-1

Now we want to study how to find the maximum and minimum values of the array at the same time with the lowest time complexity

traditional method

The easiest way to think of is to repeat the "traversal search" twice to find the maximum and minimum values respectively. Then S(n)=2(n-1) comparisons are required, but this is obviously not the best scheme.

Set the existing array a = [9,0,1,2100]

When looking for the minimum value, when traversing the second element, because 0 < 9, the minimum value is replaced with 0. At the same time, we can also know that 0 must not be the maximum value, because there is a 9 larger than it.

When looking for the maximum value, the same algorithm is adopted, resulting in 0 being compared again, and now 0 cannot be the maximum value.

optimization algorithm

Through the above traditional methods, we can find that the key to reducing the number of comparisons is to reduce unnecessary comparisons, which gives us an idea. Divide an array into k segments, find out the maximum and minimum values of the K numbers, and then compare them with the maximum and minimum values of the whole array

Suppose that the maximum and minimum values in the array with the search length of N need to be compared at most f(n) times, the array is divided into n/k segments, each segment has k numbers, and each segment needs to be compared f(k) times to obtain the maximum and minimum values, then a total of

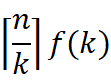
You can get n/k maximum value arrays and minimum value arrays at one time. When looking for the minimum value of the whole array, you only need to look for it from the minimum value array, and you need to compare it to find the maximum and minimum value of the whole array

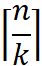
Times, so we get the function of f(n)

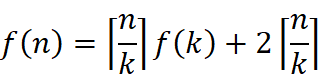
Similarly, for the array with length k, we can divide it into smaller segments until k = 2, f(2)=1, because the two numbers only need to be compared once to get the maximum and minimum value. Let's assume that the array with length n is divided into segments with length k1, and the segments with length k(i-1) are divided into smaller segments with length ki, which are brought into f(n)

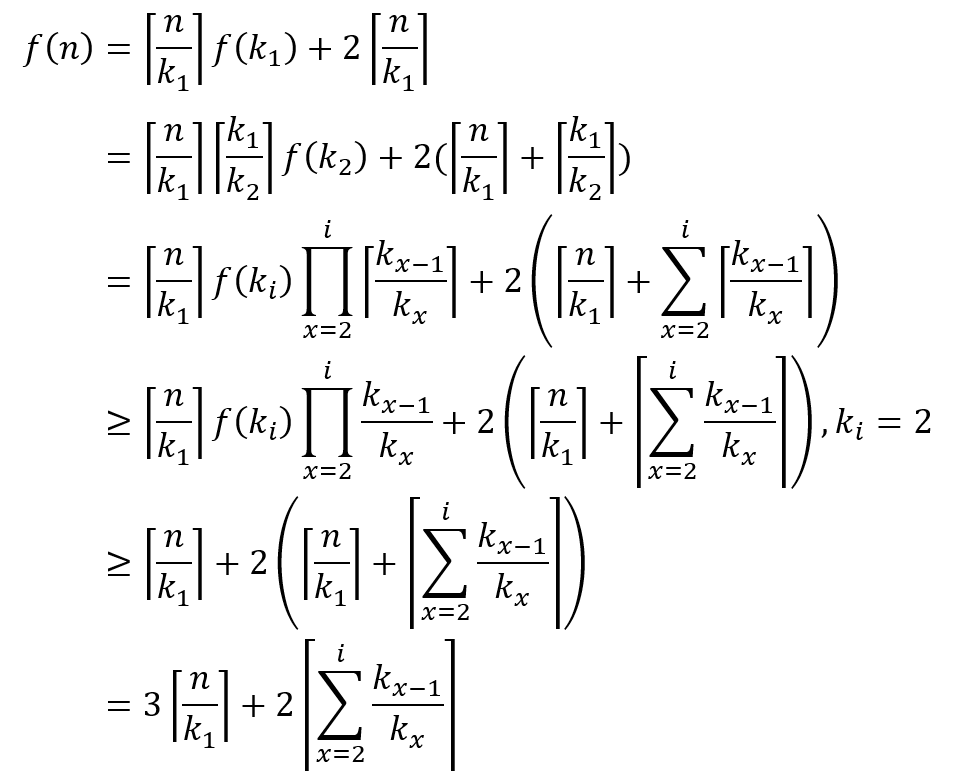
Since kx must be a positive number, when i is 1, the continuous addition on the right disappears, and f(n) takes the minimum value, that is, k1=2

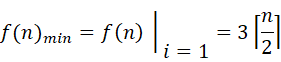
The premise of obtaining the above results is that the initial values of min and max are defined in advance, but in practical application, we can dynamically adjust the initial values according to the array. If the length is even, first compare the first two items, the large one as max and the small one as min, for a total of (3n/2-1) times; If the length is odd, both min and max take the first term, so the actual comparison times should be (3n/2-2), that is, the final comparison times should be

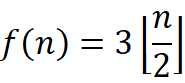
Through theory, we know that as long as the numbers in the array are compared in pairs, the smaller one is compared with the minimum value, while the larger one is compared with the maximum value, the maximum and minimum value can be obtained at the same time with the least number of comparisons

void FindMinAndMax(int* a, int len){
    int min, max, i;
    if(len % 2 == 0){
        //When the length is even, set the larger one between the first two items as the maximum value and the smaller one as the minimum value
        if(a[0] < a[1]){
            min = a[0];
            max = a[1];
        }else{
            min = a[1];
            max = a[0];
        }
        //Starting from a[2] and a[3], i is 3
        i = 3;
    }else{
        //When the length is cardinal, set the maximum and minimum values to a[0]
        min = max = a[0];
        //Starting from a[1] and a[2], i is 2
        i = 2;
    }
    while (i < len){
        if(a[i-1] < a[i]){
            if(a[i-1]<min) min = a[i-1];
            if(a[i]>max) max = a[i];
        }else{
            if(a[i]<min) min = a[i];
            if(a[i-1]>max) max = a[i-1];
        }
        i += 2;
    }
    cout << "min:" << min << endl;
    cout << "max:" << max << endl;
}

i-th order statistics

If you want to find the ith order statistic in the array, that is, the number with the smallest i, the usual way is to sort the whole array and then directly take out the number at the corresponding position. Quick sort is a good way. Quick sort divides the array into two sub arrays to sort. In fact, we only care about the number of one position, so for the two sub arrays divided by quick sort, we only need to sort one of them

int find(int *a, int left, int right, int k) {
    if (left >= right) {
        return a[left];
    }
    //key is the selected benchmark value
    int i = left, j = right, key = a[left];
    while (i < j) {
        //Traverse the array to find the first number larger than key
        while (a[i] < key) {
            ++i;
        }
        //Traverse the array to find the first number smaller than key
        while (a[j] > key) {
            --j;
        }
        //Exchange. At this time, the smaller key is on the left and the larger key is on the right
        if (i < j) {
            int temp = a[i];
            a[i] = a[j];
            a[j] = temp;
        }
    }
    //At this time, the reference value is at the ith position of the whole array
    //s is the position of the reference value in the array starting with left, and i is the position of the reference value
    int s = i - left + 1;
    if (s == k) {//If s==k, it indicates that the benchmark value is the number to be searched, and the benchmark value is returned
        return a[i];
    } else if (s > k) {//If s > k, it indicates that the reference value is on the right of the number to be searched, and the left array is traversed
        return find(a, left, j, k);
    } else {//If s < K, it means that the reference value is on the left of the number to be searched, then traverse the array on the right
        return find(a, j + 1, right, k - s);
    }
}

The comparison times of this method are affected by random factors, so it is a random algorithm. On average, its time complexity can reach O(n)