Ordinary segment tree
Problem introduction
Given that a sequence has n (n < = 100000) elements, there are the following two basic operations
Query: find the sum of all elements in a given interval [l..r]
Modify: modify the value of an element.
Task: output the value of each query.
Task quantity m (m < = 100000), only the above two operations.
Naive algorithm I
The query task can be completed using a loop, with a time complexity of O(n).
The modification task can be modified by direct assignment, and the time complexity is O(1).
The total time complexity is O(nm), timeout, unable to complete the task.
Naive algorithm II
Maintain a prefix and array sum
For query tasks, sum[r]-sum[l-1] is used, and the time complexity is O(1).
For the modified eight tasks, cycle completion is used, and the time complexity is O(n)
The total time complexity is O(nm), timeout, unable to complete the task.
Segment tree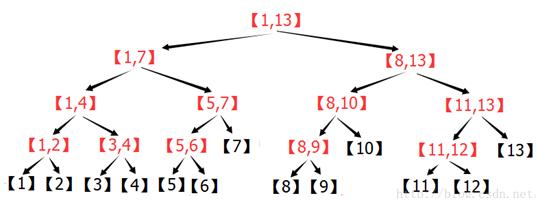
The above figure is the segment tree of interval [1-13]. Each node represents the sum of this interval. For example, [1-13] represents the sum of 1-13. It can be determined by the sum of the left subtree [1-7] and the right subtree [8-13]. Except that each interval of leaf node has these properties, leaf node is the value of a given initial array. The segment tree has the following characteristics:
1. Except for leaf nodes, each node has left and right child nodes, so the tree height is O(logn), and n is the interval length.
2. For node modification, only logn nodes are affected, and other nodes are not affected.
3. Any interval can be composed of no more than logn nodes.
I Single point modification, interval query
1. Define the meaning of nodes
struct node{
int l;// Left interval of node
int r;// Right interval of node
int sum;// Sum of nodes (sum of intervals)
} tree[Maxn<<2];// 4x
2. int sgt[maxn<<2]
Build a tree
The weight of node i = the weight of her left son + the weight of her right son.
According to this idea, we can build a tree. We set up a structure tree, tree [i] L and tree [i] R represents the left and right subscripts of the line segment represented by this point, tree [i] Sum represents the line segment and represented by this node.
We know that for a binary tree, the numbers of her left son and her right son are her * 2 and her * 2 + 1 respectively (the number of the root node is 1).
Then according to the properties just now, we get the formula: tree [i] sum=tree[i*2]. sum+tree[i*2+1]. sum; Just build a tree! The code is as follows:
inline void build(int i,int l,int r){//Recursive tree building
tree[i].l=l;tree[i].r=r;
if(l==r){//If this node is a leaf node
tree[i].sum=input[l];
return ;
}
int mid=(l+r)>>1;
build(i*2,l,mid);//Construct left subtree and right subtree respectively
build(i*2+1,mid+1,r);
tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;//The properties we just found
return ;
}
Let's summarize the query method of segment tree:
1. If this interval is completely included in the target interval, the value of this interval is returned directly
2. If the left son of this interval intersects with the target interval, search for the left son
3. If the right son of this interval intersects with the target interval, search for the right son
When you write code, it will become like this:
inline int search(int i,int l,int r){
if(tree[i].l>=l && tree[i].r<=r)//If this interval is completely included in the target interval, the value of this interval is returned directly
return tree[i].sum;
if(tree[i].r<l || tree[i].l>r) return 0;//If this interval has nothing to do with the target interval, return 0
int s=0;
if(tree[i*2].r>=l) s+=search(i*2,l,r);//If the left son of this interval intersects with the target interval, search for the left son
if(tree[i*2+1].l<=r) s+=search(i*2+1,l,r);//If the right son of this interval intersects with the target interval, search for the right son
return s;
}
Single point modification
inline void add(int i,int dis,int k){
if(tree[i].l==tree[i].r){//If it is a leaf node, it means it is found
tree[i].sum+=k;
return ;
}
if(dis<=tree[i*2].r) add(i*2,dis,k);//Where are you going
else add(i*2+1,dis,k);
tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;//Return update
return ;
}
Completion: P3374 [template] tree array 1
2, Interval modification, single point query
For interval modification and single point query, our idea becomes: if you add k to this interval, it is equivalent to painting this interval with a mark of k. then when you query at a single point, you can add up the marks along the road from the upper runway to the lower runway.
The method of labeling the interval is similar to the above interval search. The principle is the same as the three, but the first one: if the interval is completely included in the target interval, directly return the value of the interval to if the interval. If the interval is completely included in the target interval, say the interval mark k.
inline void add(int i,int l,int r,int k){
if(tree[i].l>=l && tree[i].r<=r){//If this interval is completely included in the target interval, say the interval mark k
tree[i].sum+=k;
return ;
}
if(tree[i*2].r>=l)
add(i*2,l,r,k);
if(tree[i*2+1].l<=r)
add(i*2+1,l,r,k);
}
Single point query for interval modification
void search(int i,int dis){
ans+=tree[i].num;//All the way up
if(tree[i].l==tree[i].r)
return ;
if(dis<=tree[i*2].r)
search(i*2,dis);
if(dis>=tree[i*2+1].l)
search(i*2+1,dis);
}
Completion: P3368 [template] tree array 2
3, Interval modification and interval query (core)
When interval modification is performed, if the idea of single point modification is used, the time complexity will reach O(nlogn). How to solve this problem?
We need to record a "lazy tag" lazytage to record the modification of this interval
When modifying (querying) an interval, we follow the following principles:
1. If the current interval is completely covered in the target interval, say sum+k*(tree[i].r-tree[i].l+1) of this interval
2. If it is not completely covered, the lazy flag will be sent down first
3. If the left son of this interval intersects with the target interval, search for the left son
4. If the right son of this interval intersects with the target interval, search for the right son
Interval modification of interval query
void add(int i,int l,int r,int k)
{
if(tree[i].r<=r && tree[i].l>=l)//If the current interval is completely covered in the target interval, say sum+k*(tree[i].r-tree[i].l+1) of this interval
{
tree[i].sum+=k*(tree[i].r-tree[i].l+1);
tree[i].lz+=k;//Record lazytage
return ;
}
push_down(i);//Pass down
if(tree[i*2].r>=l)
add(i*2,l,r,k);
if(tree[i*2+1].l<=r)
add(i*2+1,l,r,k);
tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;
return ;
}
The pushdown is to reset your lazytage to zero, add it to your son, and add k*(r-l+1) to your son
void push_down(int i)
{
if(tree[i].lz!=0)
{
tree[i*2].lz+=tree[i].lz;//Left and right sons plus their father's lz
tree[i*2+1].lz+=tree[i].lz;
init mid=(tree[i].l+tree[i].r)/2;
tree[i*2].data+=tree[i].lz*(mid-tree[i*2].l+1);//Sum the left and right separately
tree[i*2+1].data+=tree[i].lz*(tree[i*2+1].r-mid);
tree[i].lz=0;//Father lz returns to zero
}
return ;
}
Interval query for interval modification
inline int search(int i,int l,int r){
if(tree[i].l>=l && tree[i].r<=r)
return tree[i].sum;
if(tree[i].r<l || tree[i].l>r) return 0;
push_down(i);
int s=0;
if(tree[i*2].r>=l) s+=search(i*2,l,r);
if(tree[i*2+1].l<=r) s+=search(i*2+1,l,r);
return s;
}
Completion: P3372 [template] segment tree 1
Recommended exercises
P1204 [USACOIE] popularity of milking-
P1276 popularity of trees outside campus (enhanced version)-
P1531 I Hate It popularization / improvement-
P1198 [JSOI2008] maximum popularity / improvement-
P3870[TJOI2009] switch popularization / improvement-
P2357 popularization / improvement of tomb keepers-
P2068 statistics and popularization / improvement-
P2846 [usaco08nov] popularization / improvement of light switching G-
P1816 loyalty popularization / improvement-
P3353 popularity / improvement of stars shining outside your window-
P1168 median popularity + / improvement