Title Description

However uim, due to the purchase of some books, only M yuan (M ≤ 10000) remained in his pocket.

Although the restaurant is low-end, there are many kinds of dishes, including NN (N \le 100)(N ≤ 100), and the i sells ai ， yuan (ai ≤ 1000). As it is a very low-end restaurant, there is only one dish for each dish.

Small A pursues "never give up until he eats up all his money", so he must spend all his money on uim when he orders. He wants to know how many ways to order.

Because Xiao A is too hungry, he can only wait for 1 second at most.

Input format

The first line is two numbers, representing N and M.

N positive numbers ai from the second line (there can be the same number, and each number is within 1000).

Output format

A positive integer, indicating the number of ordering schemes, ensuring that the range of answers is within int.

Sample input and output

Enter #1

4 4
1 1 2 2

Output #1

3

Analysis: the dp problem is obvious. It looks like a 01 backpack. But it's a little different. This problem is to find the number of schemes that spend m yuan. Therefore, we can start with M. let's assume that i yuan is left for the first j items, and M yuan is left for the n items required by the topic through dp.

Sub problem analysis:

The subproblem of this problem is not as obvious as the knapsack problem, but we can know that for each item, we have two choices: buy or not. The difference between this problem and knapsack is the number of solutions. Then we can find the number of solutions dp[j][i] that cost I yuan for j items, Will be equal to the number of dp[j-1][i] schemes that do not buy this item plus the number of dp[j-1][i-p[j]] schemes that buy this item. So the subproblem is to solve dp[j-1][i] and dp[j-1][i-p[j]]

State transition:

After analyzing the sub problems, the state transition is more clear. Like 01 backpack, discuss the remaining money i. If there is enough to buy the current item, there are the above two sub problems - buy and don't buy. If it is not enough, there is only the case of not buying. At this time, the number of schemes has not changed. For this question, there is another special case, that is, if the current item can just spend the remaining money, the number of schemes at this time is one more than the first j-1 item with the same remaining money. Only buy this item. i-p[j]=0, dp[j-1][i-p[j]]=1.

At this time, for the first j items, the price of the j item is p[j] the number of schemes that need to spend I yuan dp[j][i]

The transfer equation can be obtained:

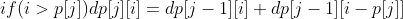
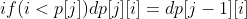
So we can get this Code:

#include<iostream>
using namespace std;

int n,m,p[122];
int used[122];
int rec[200][100000] = { 0 };
int dp[200][100000] = { 0 };
int ans = 0;
int  dfs() {//Select dep items, and now you have money
	
	for (int j = 1; j <= n; j++) {
		for (int i = 1; i <= m; i++) {
			if (i == p[j])dp[j][i] = dp[j-1][i]+1;//If the remaining money just buys the current item, there is an additional scheme to buy the item directly
			if (i > p[j])dp[j][i] = dp[j - 1][i] + dp[j - 1][i -p[j]];
			if (i < p[j])dp[j][i] = dp[j - 1][i];
		}
	}
	return dp[n][m];
}
int main() {
	cin >> n>>m;
	
	for (int j = 1; j <= n; j++) {
		//dp[j][0]=1;
		cin >> p[j];
	}
	
	cout << dfs();
}

Because the basic idea is similar to 01 knapsack, we can follow 01 knapsack for 1D space optimization:

#include<iostream>
using namespace std;
//(a*b)%c=(a%c*b%c)%c;
int n,m,p[122];
int used[122];
int rec[200][100000] = { 0 };
int dp[100000] = { 0 };
int ans = 0;
int  dfs() {//Select dep items, and now you have money

	for (int j = 1; j <= n; j++) {
		for (int i =m; i >= 1; i--) {
		if(i==p[j])dp[i]+=1;
		if(i>p[j])dp[i]+=dp[i-p[j]];
		}
	}
	return dp[m];
}
int main() {
	cin >> n>>m;
	for (int j = 1; j <= n; j++) 
		cin >> p[j];
	cout << dfs();
}

Practice a memory search:

#include<iostream>
using namespace std;

int n,m,p[122]={0};
int used[122];
int rec[200][100000] = { 0 };
int dp[200][100000] = { 0 };

int  dfs(int dep,int now) {//Select dep items, and now you have money
	if (rec[dep][now] != 0)return rec[dep][now];
    if (now == p[dep])rec[dep][now] = dfs(dep - 1, now) + 1;
	if (dep < 1||now<0)return 0;

	if(now<p[dep])
	rec[dep][now] = dfs(dep - 1, now);
	if (now >p[dep])
	rec[dep][now] = dfs(dep - 1, now)+ dfs(dep - 1, now - p[dep]) ;
	return rec[dep][now];

}
int main() {
	cin >> n>>m;
	for (int j = 1; j <= n; j++)
		cin >> p[j];

	cout << dfs(n,m);
}