Title Link: Click to enter

subject

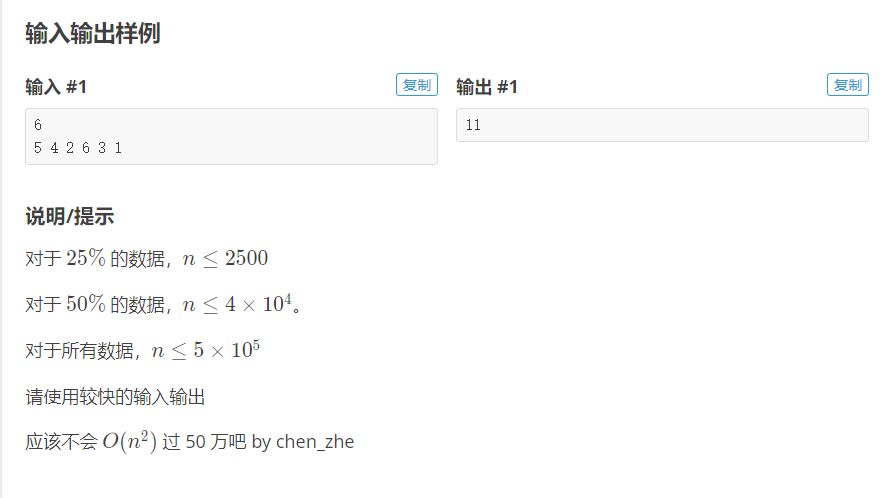
Idea 1 (tree array + discretization)

The range given by this question is 1e9. Normally, the number is used as the subscript and the corresponding value is modified. However, if the number is used as the subscript here, it will not work, because an array as large as 1e9 cannot be opened, so we discretize it (that is, sort it and assign numbers according to size). In this way, we use numbers to modify the tree array, The largest array only needs to be opened 1e6. (when you think about it carefully, discretization actually removes those positions that have not been assigned in the middle, leaving only those positions that will be used. Although these positions are renumbered, the relative positions have not changed in fact.)
Discrete end is the normal operation, for example.

Code 1

//#pragma GCC optimize(3)//O3
//#pragma GCC optimize(2)//O2
#include<iostream>
#include<string>
#include<map>
#include<set>
//#include<unordered_map>
#include<queue>
#include<cstdio>
#include<vector>
#include<cstring>
#include<stack>
#include<algorithm>
#include<iomanip>
#include<cmath>
#include<fstream>
#define X first
#define Y second
#define best 131 
#define INF 0x3f3f3f3f3f3f3f3f
#define pii pair<int,int>
#define lowbit(x) x & -x
#define inf 0x3f3f3f3f
#define int long long
//#define double long double
//#define rep(i,x,y) for(register int i = x; i <= y;++i)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const double pai=acos(-1.0);
const int maxn=1e6+10;
const int mod=1e9+7;
const double eps=1e-9;
const int N=5e3+10;
/*--------------------------------------------*/
inline int read()
{
    int k = 0, f = 1 ;
    char c = getchar() ;
    while(!isdigit(c)){if(c == '-') f = -1 ;c = getchar() ;}
    while(isdigit(c)) k = (k << 1) + (k << 3) + c - 48 ,c = getchar() ;
    return k * f ;
}
/*--------------------------------------------*/

int n,c[maxn],mp[maxn],ans;
struct node
{
	int pos;
	int num;
	bool operator < (const node&t)const
	{
		return num<t.num;
	}
}p[maxn];

void add(int x,int d)
{
	for(int i=x;i<=n;i+=lowbit(i)) c[i]+=d;
}
int getsum(int x)
{
	int sum=0;
	for(int i=x;i>=1;i-=lowbit(i)) sum+=c[i];
	return sum;
}

signed main() 
{
//	ios::sync_with_stdio(false);
//	cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>p[i].num;
		p[i].pos=i;
	}
	sort(p+1,p+n+1);
	int cnt=1;
	mp[p[1].pos]=cnt;
	for(int i=2;i<=n;i++) 
	{
		if(p[i].num==p[i-1].num)
			mp[p[i].pos]=cnt;
		else
			mp[p[i].pos]=++cnt;
	}
	for(int i=1;i<=n;i++)
	{
		ans=ans+(getsum(n)-getsum(mp[i]));
		add(mp[i],1);
	}
	cout<<ans<<endl;
    return 0;
} 

Idea 2 (segment tree + discretization)

One meaning is that the line segment tree cannot open 4e9 a space, so it is discretized (that is, it is sorted and numbered according to size). In this way, we only need to operate on the numbers after discretization, because the relative size relationship does not change, so the quantity obtained is the same.

Code 2

//#pragma GCC optimize(3)//O3
//#pragma GCC optimize(2)//O2
#include<iostream>
#include<string>
#include<map>
#include<set>
//#include<unordered_map>
#include<queue>
#include<cstdio>
#include<vector>
#include<cstring>
#include<stack>
#include<algorithm>
#include<iomanip>
#include<cmath>
#include<fstream>
#define X first
#define Y second
#define best 131 
#define INF 0x3f3f3f3f3f3f3f3f
#define pii pair<int,int>
#define lowbit(x) x & -x
#define inf 0x3f3f3f3f
#define int long long
//#define double long double
//#define rep(i,x,y) for(register int i = x; i <= y;++i)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const double pai=acos(-1.0);
const int maxn=1e6+10;
const int mod=1e9+7;
const double eps=1e-9;
const int N=5e3+10;
/*--------------------------------------------*/
inline int read()
{
    int k = 0, f = 1 ;
    char c = getchar() ;
    while(!isdigit(c)){if(c == '-') f = -1 ;c = getchar() ;}
    while(isdigit(c)) k = (k << 1) + (k << 3) + c - 48 ,c = getchar() ;
    return k * f ;
}
/*--------------------------------------------*/

int n,mp[maxn],ans;
struct node
{
	int pos;
	int num;
	bool operator < (const node&t)const
	{
		return num<t.num;
	}
}p[maxn];
struct Node
{
	int l;
	int r;
	int sum;
}t[maxn<<2];

void pushup(int p)
{
	t[p].sum=t[p<<1].sum+t[p<<1|1].sum;
}
void build(int p,int l,int r)
{
	t[p].l=l,t[p].r=r,t[p].sum=0;
	if(l==r) return ;
	int mid=l+r>>1;
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r);
	pushup(p);
}
void change(int p,int x,int d)
{
	if(t[p].l==t[p].r)
	{
		t[p].sum+=d;
		return ;
	}
	int mid=t[p].l+t[p].r>>1;
	if(x<=mid) change(p<<1,x,d);
	else change(p<<1|1,x,d);
	pushup(p);
}
int ask(int p,int l,int r)
{
	if(l<=t[p].l&&t[p].r<=r)
		return t[p].sum;
	int mid=t[p].l+t[p].r>>1,ans=0;
	if(l<=mid) ans+=ask(p<<1,l,r);
	if(r>mid) ans+=ask(p<<1|1,l,r);
	return ans;
}

signed main() 
{
//	ios::sync_with_stdio(false);
//	cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>p[i].num;
		p[i].pos=i;
	}
	
	sort(p+1,p+n+1);
	int cnt=1;
	mp[p[1].pos]=cnt;
	for(int i=2;i<=n;i++) 
	{
		if(p[i].num==p[i-1].num)
			mp[p[i].pos]=cnt;
		else
			mp[p[i].pos]=++cnt;
	}
	
	build(1,1,cnt);
	for(int i=1;i<=n;i++)
	{
		change(1,mp[i],1);
		ans=ans+(i-ask(1,1,mp[i]));
	}
	cout<<ans<<endl;
    return 0;
} 

Train of thought 3 (line segment tree + dynamic open point)

If the space cannot be opened 4e9 by the line segment tree, we can consider the dynamic opening point, that is, for those nodes we do not use, we do not give it space, but only give them useful point space. For this way of using only the open point, it means that the child nodes cannot be accessed through P < < 1, P < < 1|1, and the numbers become out of order. That is, t [P] l , t [ p ]. r stores the subscripts of the left and right children, but the numbers are in disorder, which are added when we need to use them.
(Note: the & before subscript p in the update function cannot be omitted)
The dynamic opening point is used here, which can be directly 1~1e9 operated without discretization.

Code 3

//#pragma GCC optimize(3)//O3
//#pragma GCC optimize(2)//O2
#include<iostream>
#include<string>
#include<map>
#include<set>
//#include<unordered_map>
#include<queue>
#include<cstdio>
#include<vector>
#include<cstring>
#include<stack>
#include<algorithm>
#include<iomanip>
#include<cmath>
#include<fstream>
#define X first
#define Y second
#define best 131 
#define INF 0x3f3f3f3f3f3f3f3f
#define pii pair<int,int>
#define lowbit(x) x & -x
#define inf 0x3f3f3f3f
//#define int long long
//#define double long double
//#define rep(i,x,y) for(register int i = x; i <= y;++i)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const double pai=acos(-1.0);
const int maxn=1e7+10;
const int mod=1e9+7;
const double eps=1e-9;
const int N=5e3+10;
/*--------------------------------------------*/
inline int read()
{
    int k = 0, f = 1 ;
    char c = getchar() ;
    while(!isdigit(c)){if(c == '-') f = -1 ;c = getchar() ;}
    while(isdigit(c)) k = (k << 1) + (k << 3) + c - 48 ,c = getchar() ;
    return k * f ;
}
/*--------------------------------------------*/

int n,a[maxn],root,cnt,limit;
ll ans;
struct node
{
	int l;
	int r;
	int sum;
}t[maxn];

void pushup(int p)
{
	t[p].sum=t[t[p].l].sum+t[t[p].r].sum;
}
void change(int &p,int l,int r,int x,int d)
{
	if(!p) p=++cnt;
	if(l==r)
	{
		t[p].sum+=d;
		return ;
	}
	int mid=l+r>>1;
	if(x<=mid) change(t[p].l,l,mid,x,d);
	else change(t[p].r,mid+1,r,x,d);
	pushup(p);
}
int ask(int p,int l,int r,int x,int y)
{
	if(!p) return 0;
	if(x<=l&&r<=y)
		return t[p].sum;
	int mid=l+r>>1,ans=0;
	if(x<=mid) ans+=ask(t[p].l,l,mid,x,y);
	if(y>mid) ans+=ask(t[p].r,mid+1,r,x,y);
	return ans;
}

int main() 
{
//	ios::sync_with_stdio(false);
//	cin.tie(0);cout.tie(0);
	limit=1e9;
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i<=n;i++)
	{
		change(root,1,limit,a[i],1);
		ans=ans+(i-ask(root,1,limit,1,a[i]));
	}
	cout<<ans<<endl;
    return 0;
}