This series of articles is the study notes of data structure of Chen Yue and he Qinming of Zhejiang University. The links of the previous series of articles are as follows:
Fundamentals of data structure: P1 - Basic Concepts
Basic data structure: P2 1 - linear structure - > linear table
Basic data structure: P2 2-linear structure - > stack
Basic data structure: P2 3-linear structure - > queue
Basic data structure: P2 4 - application example - > polynomial addition operation

1, Topic meaning understanding and polynomial representation

1.1 topic meaning understanding

Title: design function to find the product and sum of two univariate polynomials respectively
( 1 ) 3 x 4 − 5 x 2 + 6 x − 2 (1)3{x^4} - 5{x^2} + 6x - 2 (1)3x4−5x2+6x−2
( 2 ) 5 x 20 − 7 x 4 + 3 x (2)5{x^{20}} - 7{x^4} + 3x (2)5x20−7x4+3x
Input example: first enter the number of polynomial terms, and then enter various coefficients and exponents in turn.
4 3 4 -5 2 6 1 -2 0
3 5 20 -7 4 3 1

Polynomial ① has 4 terms and polynomial ② has 3 terms. There are 7 items in total, and then there are 5 items after merging similar items. The results are as follows:
5 x 20 − 4 x 4 − 5 x 2 + 9 x − 2 5{x^{20}} - 4{x^4} - 5{x^2} + 9x - 2 5x20−4x4−5x2+9x−2
Polynomial ① has 4 terms and polynomial ② has 3 terms. There are 12 items multiplied, and then there are items after merging similar items. The results are as follows:
15 x 24 − 25 x 22 + 30 x 21 − 10 x 20 − 21 x 8 + 35 x 6 − 33 x 5 + 14 x 4 − 15 x 3 + 18 x 2 − 6 x {\rm{15}}{x^{24}}{\rm{ - 25}}{x^{22}}{\rm{ + 30}}{x^{21}}{\rm{ - 10}}{x^{20}}{\rm{ - 21}}{x^8}{\rm{ + 35}}{x^6}{\rm{ - 33}}{x^5}{\rm{ + 14}}{x^4}{\rm{ - 15}}{x^3}{\rm{ + 18}}{x^2}{\rm{ - 6}}x 15x24−25x22+30x21−10x20−21x8+35x6−33x5+14x4−15x3+18x2−6x

Output example: output the result of polynomial multiplication (the first line) and the result of addition (the second line) from large to small according to the coefficient:
15 24 -25 22 30 21 -10 20 -21 8 35 6 -33 5 14 4 -15 3 18 2 -6 1
5 20 -4 4 -5 2 9 1 -2 0

1.2 polynomial representation

Our solution idea is as follows:

1. Polynomial representation
2. Procedural framework
3. Read polynomial
4. Additive implementation
5. Multiplication implementation
6. Polynomial output

Polynomial representation:
The core of the representation of polynomials is to represent the key information of Polynomials: the coefficients and exponents of non-zero terms. This one-to-one information should be expressed, which is a linear sequence. There are two storage methods on the linear sequence computer: array and linked list.

array
The array method is relatively simple and easy to debug, but the size of the array must be determined in advance. When you don't know the number of terms of this polynomial in advance, we can only express it with the maximum possible number of terms. In fact, there may not be so many pixels, which will cause a waste of space.
Linked list
The linked list method just overcomes the disadvantage of array. It doesn't need to know how many items there are in advance. I'll deal with one for you and insert it into the linked list as a node. Therefore, its advantage is that it is dynamic, but the program will be more complex, involving pointers, and debugging is also more difficult.
Note: for this problem, there is a better implementation method: dynamic array. But in order to train everyone's programming ability in linked list, we still use linked list here.

Data structure design:
The linked list is composed of several nodes. The node information: coefficient, index and pointer to the next node.

typedef struct PolyNode *Polynomial;
struct PolyNode {
	int coef;
	int expon;
	Polynomial link;
};

The first two polynomials are represented by a linked list, and their structure is shown in the figure below:

2, Program framework and read polynomial

2.1 procedure framework

According to the requirements of our program programming, the framework of our whole program is roughly as follows.

int main()
{
	Read in polynomial 1
	Read in polynomial 2
	Multiply and output
	Add and output
	return 0;
}

We want to design some functions to assist the completion of our whole program. What functions should we design?

Functions to be designed:
• Read a polynomial
• Multiplication of two polynomials
• Addition of two polynomials
• Polynomial output

According to such an idea, the main process of our main function is as follows:

① First, we define several variables, in which P1 and P2 respectively represent the polynomials of the two inputs, so we read the two polynomials through ReadPoly and return the pointers of P1 and P2.
② Then pass the two pointers to the function Mult for multiplication. The result of multiplication is also a linked list, so the returned pointer is a structure.
③ Next, we need to output this polynomial, so just transfer the head of the linked list as a parameter to the function PrintPoly, and he will output the polynomial.
④ We also need to Add, so pass P1 and P2 into the Add function as parameters.
⑤ After the addition operation, the pointer to the node of a new polynomial is returned. I Print the polynomial of this sum.

The corresponding codes are as follows:

int main()
{
	Polynomial P1, P2, PP, PS;
	P1 = ReadPoly();
	P2 = ReadPoly();
	PP = Mult( P1, P2 );
	PrintPoly( PP );
	PS = Add( P1, P2 );
	PrintPoly( PS );
	return 0;
}

2.2 reading polynomials

After having this framework, let's first look at how to read polynomials. The corresponding code structure is as follows:

Polynomial ReadPoly()
{
	......
	scanf("%d", &N);
	......
	while ( N-- ) {
		scanf("%d %d", &c, &e);
		Attach(c, e, &Rear);
	}
	......
	return P;
}

Next, let's analyze its structure in detail:

The format of the number required by the title is as follows:
4 3 4 -5 2 6 1 -2 0
The first integer represents how many terms he has, followed by a pair of coefficient exponents. So for the program of reading polynomials, he should first read the integer, and then read the coefficients and exponents one-to-one. Therefore, our whole program framework is as follows:
① First, use scanf to read in this 4 and assign it to the variable N
② Next, make a four-wheel cycle, and then use the form of while (N –) to control the number of cycles.
③ Then what is to be done in each cycle? The coefficient exponent is read in and put into c and e respectively, so as to construct a node and insert this node into the polynomial. The reading process is carried out in exponential descending order, so when reading a new node, it should be inserted after the previous node.
Therefore, finally, we form such a linked list that P1 points to:

There are some key issues in the above analysis:
1. The new node should be inserted behind the original result, so we need a pointer, Rear, to represent the last term of the current result polynomial, so that a node constructed later can find the last term and insert it behind it. The insertion process is completed through the function Attach. In this process, we should note that Rear originally points to the end of a linked list. After you insert a new node, the new node becomes the last item in the linked list. Therefore, real should refer to the new node, which means that the variable of real must be changed in the Attach function. Therefore, we need to pass the address of real into the Attach function.

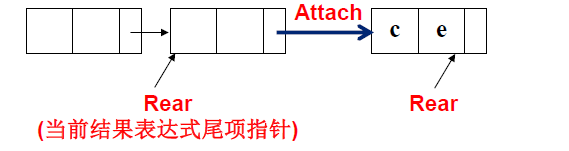
2. We say that Rear refers to the last item of the result index. What is the value of Rear at the beginning? There are two ways to deal with it

① The real is set to NULL at the beginning. In the Attach function, different processing is performed according to whether the real is NULL or not
When the Rear is NULL, it indicates that it is the first node at the beginning. At this time, apply for this node, and then point the Rear to this node. If the Rear value is not NULL, we will directly insert the new node after the Rear.
② At first, we construct an empty node, and then let the Rear value point to the empty node. In the future, all newly inserted nodes are inserted behind the Rear.
If such a method is used for processing, it is not necessary to judge whether real is NULL in the Attach function. This is a method of temporarily applying for an empty node, which makes the processing of the program more consistent and the code simpler. Of course, in the end, you must delete this empty node.

According to the idea of creating an empty node above, the Attach function is designed as follows:

void Attach( int c, int e, Polynomial *pRear )
{ 
	Polynomial P;
	P = (Polynomial)malloc(sizeof(struct PolyNode));
	P->coef = c; /* Assign value to new node */
	P->expon = e;
	P->link = NULL;
	(*pRear)->link = P;
	*pRear = P; /* Modify prar value */
}

According to the previous analysis, we read the complete program of Polynomials:

Polynomial ReadPoly()
{
	Polynomial P, Rear, t;
	int c, e, N;
	scanf("%d", &N);
	P = (Polynomial)malloc(sizeof(struct PolyNode)); /* Linked list header empty node */
	P->link = NULL;
	Rear = P;
	while ( N-- ) {
		scanf("%d %d", &c, &e);
		Attach(c, e, &Rear); /* Inserts the current item at the end of the polynomial */
	}
	t = P; P = P->link; free(t); /* Delete temporarily generated header node */
	return P;
}

3, Addition, multiplication and polynomial output

3.1 addition operation

Polynomial addition operation has been mentioned earlier. The specific steps are as follows:

① We can start by pointing to these two polynomials with T1 and T2, respectively. Next, for the convenience of processing, we first construct an empty node, which can insert these items of T1 and T2 later
② When T1 and T2 are not empty, a while loop is used to compare the index pointed to by the current T1 and T2. If the exponent is equal, add the coefficients, and then see if it is equal to 0. If it is equal to 0, it doesn't matter. If it is not equal to 0, add the new coefficient and index to Rear. Finally, T1 and T2 move back respectively. If the exponents pointed to by T1 and T2 are not equal, let's compare which is larger and copy the larger one to the back of Rear. This loop keeps doing as long as both polynomials are not empty.
③ When t1 t2 has an empty space, the loop exits. After you exit, you should connect all the other ones that may not be empty to the back of the Rear. Therefore, two while loops are used to deal with the cases where t1 is not empty and t2 is not empty. Then finally return the head of the polynomial.

The corresponding code of addition operation is as follows:

Polynomial Add(Polynomial P1, Polynomial P2)
{
	Polynomial t1 = P1;
	Polynomial t2 = P2;
	Polynomial temp;
	Polynomial P = (Polynomial)malloc(sizeof(struct PolyNode)); P->link = NULL;
	Polynomial Rear = P;
	int sum;

	while (t1 && t2) {
		if (t1->expon == t2->expon) {
			sum = t1->coef + t2->coef; //Record the coefficients of these two terms
			if (sum) Attach(sum, t1->expon, &Rear); //If the coefficient addition is not 0, after receiving the rear
			t1 = t1->link; //P1 and P2 move back
			t2 = t2->link;
		}
		else if (t1->expon > t2->expon) {
			Attach(t1->coef, t1->expon, &Rear);
			t1 = t1->link;
		}
		else {
			Attach(t2->coef, t2->expon, &Rear);
			t2 = t2->link;
		}
	}
	while (t1) {
		Attach(t1->coef, t1->expon, &Rear);
		t1 = t1->link;
	}
	while (t2) {
		Attach(t2->coef, t2->expon, &Rear);
		t2 = t2->link;
	}

	Rear->link = NULL;
	temp = P;
	P = P->link; /*Let front point to the first nonzero term of the resulting polynomial */
	free(temp); /* Release temporary space-time header node */

	return P;
}

3.2 multiplication

There are two ways to multiply two polynomials.

1. Convert multiplication to addition
Convert multiplication to addition, multiply P1 current term (ci,ei) by P2 polynomial, and then add up these results.

t1 = P1; t2 = P2; 
P = (Polynomial)malloc(sizeof(struct PolyNode)); P->link = NULL; 
Rear = P; 
while (t2) { 
	Attach(t1->coef*t2->coef, t1->expon+t2->expon, &Rear); 
	t2 = t2->link; 
}

2. Insert item by item
Set P1 to the current item ( c 1 i , e 1 i ) {\rm{(c}}{{\rm{1}}_{\rm{i}}}{\rm{,e}}{{\rm{1}}_{\rm{i}}}{\rm{)}} (c1i, e1i) multiply P2 current item ( c 2 i , e 2 i ) {\rm{(c}}{{\rm{2}}_{\rm{i}}}{\rm{,e}}{{\rm{2}}_{\rm{i}}}{\rm{)}} (c2i, e2i) and inserted into the resulting polynomial. The initial result polynomial can be obtained by multiplying the first term of P1 by P2. Next, multiply the current term of P1 by the current term of P2 and insert it step by step. The specific code is as follows:

Polynomial Mult(Polynomial P1, Polynomial P2)
{
	Polynomial P, Rear, t1, t2, t;
	int c, e;
	if (!P1 || !P2) return NULL;
	t1 = P1; t2 = P2;
	P = (Polynomial)malloc(sizeof(struct PolyNode)); P->link = NULL;
	Rear = P;
	while (t2) { /* First multiply the first term of P1 by P2 to obtain P */
		Attach(t1->coef*t2->coef, t1->expon + t2->expon, &Rear);
		t2 = t2->link;
	}
	t1 = t1->link;
	//Double loop, multiply each term of t1 by each term of t2
	while (t1) {
		t2 = P2; Rear = P;
		while (t2) {
			e = t1->expon + t2->expon; //Exponential addition, coefficient multiplication
			c = t1->coef * t2->coef;
			while (Rear->link && Rear->link->expon > e) //If the current coefficient is small, the Rear moves back
				Rear = Rear->link;
			if (Rear->link && Rear->link->expon == e) {//If the exponents are equal, the coefficients are added
				if (Rear->link->coef + c)
					Rear->link->coef += c;
				else {  //The coefficients add up to 0 and delete it
					t = Rear->link;
					Rear->link = t->link;
					free(t);
				}
			}
			else { //If the exponents are not equal, insert them
				t = (Polynomial)malloc(sizeof(struct PolyNode));
				t->coef = c; t->expon = e;
				//Start insertion
				t->link = Rear->link;
				Rear->link = t; Rear = Rear->link;
			}
			t2 = t2->link;
		}
		t1 = t1->link;
	}
	//Delete the initial null node and let the returned pointer point to the first term of the result polynomial
	t2 = P; P = P->link; free(t2);

	return P;
}

3.3 polynomial output

Polynomial output is actually a linked list traversal problem, traversing each item of the linked list and outputting the corresponding coefficients and exponents.

void PrintPoly(Polynomial P)
{ /* Output polynomial */
	int flag = 0; /* For auxiliary adjustment of output format */
	if (!P) { printf("0 0\n"); return; }
	while (P) {
		if (!flag)
			flag = 1;
		else
			printf(" ");
		printf("%d %d", P->coef, P->expon);
		P = P->link;
	}
	printf("\n");
}

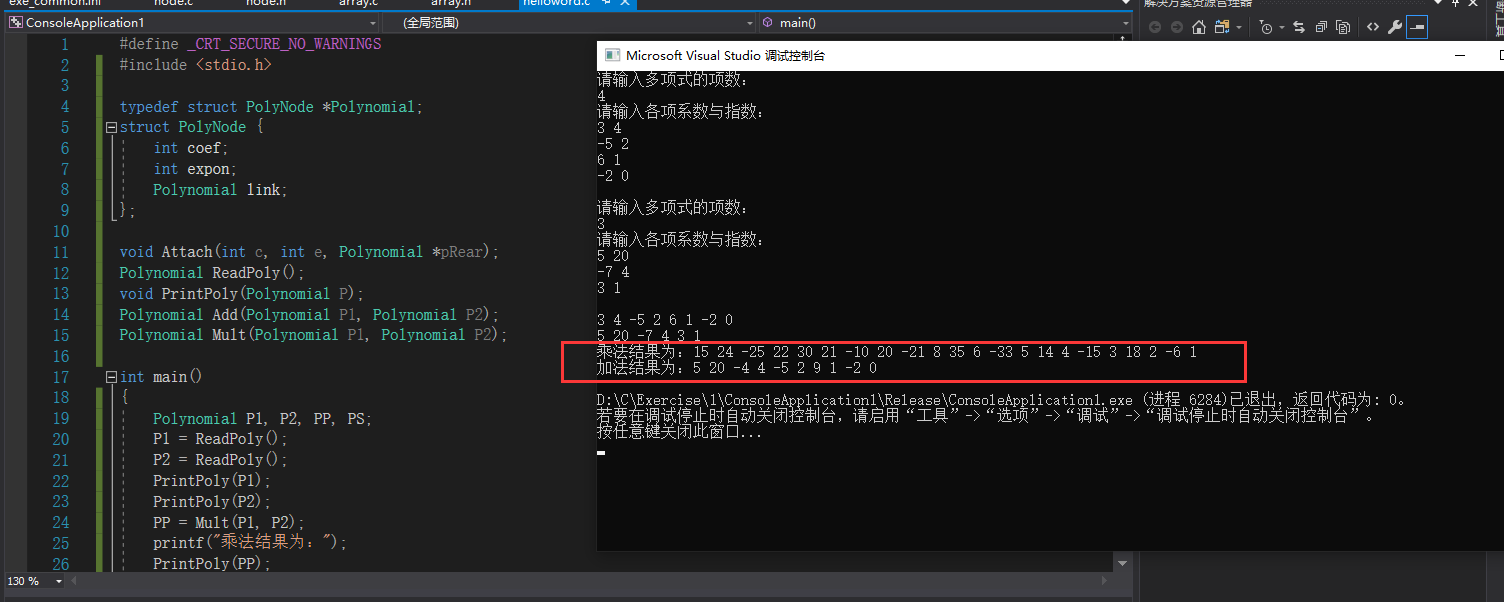
4, Overall code and test results

The overall code is as follows:

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>

typedef struct PolyNode *Polynomial;
struct PolyNode {
	int coef;
	int expon;
	Polynomial link;
};

void Attach(int c, int e, Polynomial *pRear);
Polynomial ReadPoly();
void PrintPoly(Polynomial P);
Polynomial Add(Polynomial P1, Polynomial P2);
Polynomial Mult(Polynomial P1, Polynomial P2);

int main()
{
	Polynomial P1, P2, PP, PS;
	P1 = ReadPoly();
	P2 = ReadPoly();
	PrintPoly(P1);
	PrintPoly(P2);
	PP = Mult(P1, P2);
	printf("The multiplication result is:");
	PrintPoly(PP);
	PS = Add(P1, P2);
	printf("The addition result is:");
	PrintPoly(PS);

	return 0;
}


void Attach(int c, int e, Polynomial *pRear)
{
	Polynomial P;
	P = (Polynomial)malloc(sizeof(struct PolyNode));
	P->coef = c; /* Assign value to new node */
	P->expon = e;
	P->link = NULL;
	(*pRear)->link = P;
	*pRear = P; /* Modify prar value */
}

Polynomial ReadPoly()
{
	Polynomial P, Rear, t;
	int c, e, N;
	printf("Please enter the number of items of polynomial:\n");
	scanf("%d", &N);
	P = (Polynomial)malloc(sizeof(struct PolyNode)); /* Linked list header empty node */
	P->link = NULL;
	Rear = P;
	printf("Please enter the coefficients and indices:\n");
	while (N--) {
		scanf("%d %d", &c, &e);
		Attach(c, e, &Rear); /* Inserts the current item at the end of the polynomial */
	}
	printf("\n");
	t = P; P = P->link; free(t); /* Delete temporarily generated header node */
	return P;
}

Polynomial Add(Polynomial P1, Polynomial P2)
{
	Polynomial t1 = P1;
	Polynomial t2 = P2;
	Polynomial temp;
	Polynomial P = (Polynomial)malloc(sizeof(struct PolyNode)); P->link = NULL;
	Polynomial Rear = P;
	int sum;

	while (t1 && t2) {
		if (t1->expon == t2->expon) {
			sum = t1->coef + t2->coef; //Record the coefficients of these two terms
			if (sum) Attach(sum, t1->expon, &Rear); //If the coefficient addition is not 0, after receiving the rear
			t1 = t1->link; //P1 and P2 move back
			t2 = t2->link;
		}
		else if (t1->expon > t2->expon) {
			Attach(t1->coef, t1->expon, &Rear);
			t1 = t1->link;
		}
		else {
			Attach(t2->coef, t2->expon, &Rear);
			t2 = t2->link;
		}
	}
	while (t1) {
		Attach(t1->coef, t1->expon, &Rear);
		t1 = t1->link;
	}
	while (t2) {
		Attach(t2->coef, t2->expon, &Rear);
		t2 = t2->link;
	}

	Rear->link = NULL;
	temp = P;
	P = P->link; /*Let front point to the first nonzero term of the resulting polynomial */
	free(temp); /* Release temporary space-time header node */

	return P;
}

Polynomial Mult(Polynomial P1, Polynomial P2)
{
	Polynomial P, Rear, t1, t2, t;
	int c, e;
	if (!P1 || !P2) return NULL;
	t1 = P1; t2 = P2;
	P = (Polynomial)malloc(sizeof(struct PolyNode)); P->link = NULL;
	Rear = P;
	while (t2) { /* First multiply the first term of P1 by P2 to obtain P */
		Attach(t1->coef*t2->coef, t1->expon + t2->expon, &Rear);
		t2 = t2->link;
	}
	t1 = t1->link;
	while (t1) {
		t2 = P2; Rear = P;
		while (t2) {
			e = t1->expon + t2->expon;
			c = t1->coef * t2->coef;
			while (Rear->link && Rear->link->expon > e)
				Rear = Rear->link;
			if (Rear->link && Rear->link->expon == e) {
				if (Rear->link->coef + c)
					Rear->link->coef += c;
				else {
					t = Rear->link;
					Rear->link = t->link;
					free(t);
				}
			}
			else {
				t = (Polynomial)malloc(sizeof(struct PolyNode));
				t->coef = c; t->expon = e;
				t->link = Rear->link;
				Rear->link = t; Rear = Rear->link;
			}
			t2 = t2->link;
		}
		t1 = t1->link;
	}
	t2 = P; P = P->link; free(t2);

	return P;
}

void PrintPoly(Polynomial P)
{ /* Output polynomial */
	int flag = 0; /* For auxiliary adjustment of output format */
	if (!P) { printf("0 0\n"); return; }
	while (P) {
		if (!flag)
			flag = 1;
		else
			printf(" ");
		printf("%d %d", P->coef, P->expon);
		P = P->link;
	}
	printf("\n");
}

Run, input the test sample given in the title, and the result is correct: