Title portal P2081

Some definitions:

Define that \ (fa_ \) represents the father of \ (u \), \ (facet_ \) represents the number of parent nodes of \ (u \) (value \ (1 \) or \ (2 \)), \ (son_ \) represents the number of sons of \ (u \), \ (ch_ \) represents the child nodes of \ (u \), and \ (down_ \) represents the expected path length starting from \ (u \) in the tree with \ (1 \) as the root\ (up_ \) represents the expected path length from \ (u \) to the first step upward, \ (w_{i,j} \) represents the edge weight from \ (i \) to \ (j \).

Then for each point, the answer is \ (ans_ = \ dfrac {1} {son_ + facnt_} \ times (son_ \ times down_ + up_ \ times facnt_) \).

The final answer is \ u {limit} \.

50pts is divided into two parts (the picture shows a tree):

At this time \ (facet_ = 1 \). Therefore, the \ (down \) value does not depend on the \ (up \) value. The derivation is relatively simple:

For the value of \ (up \), you need to rely on \ (down {FA} \) and \ (up {FA} \). At this time, we must go to \ (fa_ \) in the first step, and we can't go back to \ (u \) in the next step. Then the formula is derived:

So we can get a good score of \ (50 \tt pts \).

In addition, 50pts (the figure shows a base ring tree):

We regard the base ring tree as the result of some trees connecting into a ring. The nodes on the ring are hereinafter referred to as "ring points", and the rest are "tree points". As shown in the figure, it is a base ring tree, in which each node is connected to its parent node.

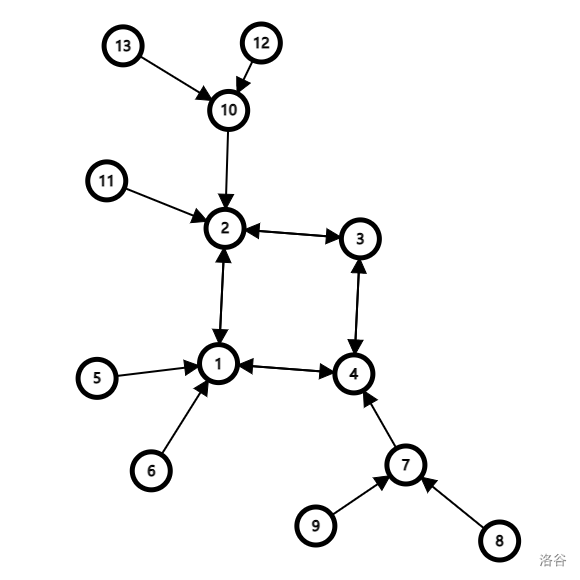
All ring points \ (facnt=2 \) and tree points \ (facnt=1 \).

First, by definition, the \ (down \) value of each point remains unchanged. The calculation of \ (up \) value is more troublesome.

Secondly, considering the derivation process, the \ (up \) value of each tree point can still be obtained by the above formula. For the ring point, it is more troublesome, because at each step, we can choose to go to a ring point or into the subtree of the current ring point.

We first find some values through traversal (because we need to perform the following calculation, and we need to connect these ring points in order to ensure that they are found, which is exactly the ring in the original figure):

• \(t \), indicating the number of loop points.
• \(dfn_ \), indicating that this point is the first ring point found.
• \(id_i \), indicating the label of the \ (I \) ring point found.
• \(disl_i, \, disr_i \), which represents the left and right edge weights of the \ (I \) found ring point on the ring.

For a loop point \ (u \), we force it to walk counterclockwise on the loop, then its \ (up \) value formula is:

The values of \ (i \) are \ (dfn_u + 1, \, dfn_ + 2, \, \ ldots T, \, 1, \, \ ldots dfn_ - 1 \). Although it looks strange, it is indeed this formula.

Where \ (p_i \) represents the probability of reaching this loop point. Since we limit that the first step does not enter the subtree, so \ (p_ {dfn_ \ bmod T + 1} = 1 \). For each ring point, we have a chance to enter its subtree or continue walking on the ring, so \ (p_{i \bmod t + 1} = p_i \times \dfrac{1}{son_{id_i} + 1} \)\ (w \) represents the edge weight from the previous loop point. It should be noted that if the next ring point has passed counterclockwise (i.e. one circle), we can only enter the subtree of that point.

The above specifies that the first step goes counterclockwise, and the clockwise is the same. The sum of the two \ (up \) values \ (/ 2 \) is the final \ (up \) value. Or directly set \ (p_{dfn_ \ bmod T + 1} \) to \ (\ dfrac12 \).

Finally, update the \ (up \) value of each tree point. The total complexity is \ (O(n + k^2) \), \ (k \) is the number of ring points.

#define pii pair<int, int>
#define Ld double
#define pb push_back
#define mp make_pair

int n, m;
vector<pii > e[N];

namespace Tree {
	Ld f[N], g[N];
	
	void dfs(int u, int Fa) {
		int nw = 0;
		for(pii x : e[u]) {
			int v = x.fi, w = x.se;
			if(v == Fa) continue;
			++nw;
			dfs(v, u);
			f[u] += f[v] + w;
		}
		if(nw) f[u] /= nw;
	}
	
	void dfs2(int u, int Fa) {
		for(pii x : e[u]) {
			int v = x.fi, w = x.se;
			if(v == Fa) continue;
			if(e[u].size() == 1) g[v] = w;
			else g[v] = w + (g[u] + f[u] * (e[u].size() - (u != 1)) - f[v] - w) / (e[u].size() - 1);
			dfs2(v, u);
		}
	}
	
	void solve() {
		dfs(1, 0);
		dfs2(1, 0);
		Ld ans = 0.0;
		rep(i, 1, n) {
			ans += (f[i] * (e[i].size() - (i != 1)) + g[i]) / e[i].size();
		}
		printf("%.5f\n", ans / n);
	}
}

int t, pos, fl;
int facnt[N], son[N];
int id[N], dfn[N];
int disl[N], disr[N];
bool vis[N];
Ld f[N], g[N];

void dfs(int u, int Fa) {
	vis[u] = 1;
	for(pii x : e[u]) {
		int v = x.fi;
		if(v == Fa) continue;
		if(vis[v]) {
			pos = v;
			return ;
		}
		dfs(v, u);
		if(!fl && pos) {
			if(pos == u) fl = 1;
			return ;
		}
		if(fl) break;
	}
	vis[u] = 0;
}

void dfs2(int u, int Fa) {
	id[++t] = u; dfn[u] = t;
	for(pii x : e[u]) {
		int v = x.fi, w = x.se;
		if(dfn[v] || !vis[v] || v == Fa) continue;
		disr[t] = disl[t + 1] = w;
		dfs2(v, u);
	}
}

void down(int u, int Fa) {
	int cnt = 0;
	for(pii x : e[u]) {
		int v = x.fi, w = x.se;
		if(vis[v] || v == Fa) continue;
		++cnt;
		down(v, u);
		f[u] += f[v] + w;
	}
	if(son[u] = cnt) f[u] /= cnt;
}

void up(int u, int Fa) {
	for(pii x : e[u]) {
		int v = x.fi, w = x.se;
		if(vis[v] || v == Fa) continue;
		g[v] = w;
		if(facnt[u] + son[u] - 1) g[v] += (g[u] * facnt[u] + f[u] * son[u] - f[v] - w) / (facnt[u] + son[u] - 1); 
		up(v, u);
	}
}

int pre(int x) { return x == 1 ? t : x - 1; }
int nxt(int x) { return x == t ? 1 : x + 1; }

void solve() {
	dfs(1, 0); // Mark the vis of all loop points as 1
	rep(i, 1, n) if(vis[i]) facnt[i] = 2; else facnt[i] = 1;
	dfs2(pos, 0);
	for(pii x : e[id[1]]) if(x.fi == id[t]) {
		disl[1] = disr[t] = x.se;
		break;
	}
	rep(i, 1, t) down(id[i], 0);
	rep(i, 1, t) {
		int u = id[i];
		Ld p = 0.5;
		int j = nxt(i); while(j != i) {
			int v = id[j], w = disl[j];
			if(nxt(j) == i) g[u] += p * (f[v] + w);
			else g[u] += p * (f[v] * son[v] / (son[v] + 1) + w);
			p /= son[v] + 1;
			j = nxt(j);
		}
		p = 0.5;
		j = pre(i); while(j != i) {
			int v = id[j], w = disr[j];
			if(pre(j) == i) g[u] += p * (f[v] + w);
			else g[u] += p * (f[v] * son[v] / (son[v] + 1) + w);
			p /= son[v] + 1;
			j = pre(j);
		}
	}
	rep(i, 1, t) up(id[i], 0);
	Ld ans = 0.0;
	rep(i, 1, n) ans += (facnt[i] * g[i] + son[i] * f[i]) / (son[i] + facnt[i]);
	printf("%.5f\n", ans / n);
}

int main() {
	qread(n, m);
	rep(i, 1, m) {
		int u, v, w;
		qread(u, v, w);
		e[u].pb(mp(v, w));
		e[v].pb(mp(u, w));
	}
	if(m == n - 1) Tree::solve();
	else solve(); // Base ring tree
	return 0;
}