Title Description

There is a matrix composed of integers of (a*b) from which you can find a square area of (n*n\\\\\\\\\

Input and output format

Input format:

The first behavior(3) integers represent the values of(a,b,n)

From the second line to the (a+1) line, each action (b) is a non-negative integer representing the number at the corresponding position in the matrix. Each row is separated by a space between two adjacent numbers.

Output format:

Only one integer is the minimum of the difference between the largest integer and the smallest integer in all (n*n\) square areas of the \\\\\\\\

\(Solution\)

This question is not serious \\\\\\\\\\\\
As a result, I finally looked at the solution, (woc?) monotone queue, and found that it was actually very simple.
As long as monotonic queues are made in each row, a matrix is formed.
Then the final matrix can be formed by monotonic queues for each column, i n which only statistics(\Sigma_i^{n-k+1}Sigma_j^{m-k+1} Max (ans, Ymax [i] [j]-Ymin [i] [j]])are needed.
Imaginally, make a monotonic queue for each row, and let(xmax[i][j] denote the maximum value of(j~j+k-1) in line(i)
Then, by rotating the resulting matrix, the one-dimensional operation that has not yet been compressed will be operated as above.
The following is an illustration, turned from \(luogu\) problem solving, in which \[[[[]][[[]]] \[[[[[]][[[[[]]] \[[[[[]][[]]][[[[]]]\[[[[[[[[]]][[[[[[[[[]]]]]\\[[[[[[[[]][[[[]]\[[[[[]]]]\\\].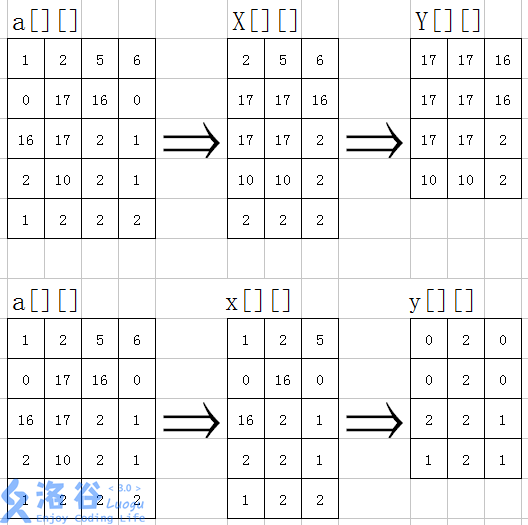

Note that monotonic queues are subscripts to stored weights, which are monotonic. This is the conventional monotone queue writing, of course, you can also open a structure storage weight + subscript.
Then you just need to start with (2) because there is no (k=1)

\(Code\)

#include<cstdio>
#include<iostream>
#define maxn 1010
#define re register

using namespace std;

int ans=0x7fffffff,front1,back1,front2,back2;
int a[maxn][maxn],q1[maxn],q2[maxn];
int xmax[maxn][maxn],xmin[maxn][maxn];
int ymax[maxn][maxn],ymin[maxn][maxn];
int n,m,k;
int main()
{
    scanf("%d%d%d",&n,&m,&k);
    for(re int i=1;i<=n;++i)
     for(re int j=1;j<=m;++j)
      scanf("%d",&a[i][j]);
    for(re int i=1;i<=n;++i)
    {
        front1=front2=back1=back2=q1[1]=q2[1]=1;
        for(re int j=2;j<=m;++j)
        {
            while(a[i][j]>=a[i][q1[back1]]&&front1<=back1) back1--;
            while(a[i][j]<=a[i][q2[back2]]&&front2<=back2) back2--;
            back1++,back2++;
            q1[back1]=j,q2[back2]=j;
            while(j-q1[front1]>=k) front1++;
            while(j-q2[front2]>=k) front2++;
            if(j>=k) xmax[i][j-k+1]=a[i][q1[front1]],xmin[i][j-k+1]=a[i][q2[front2]];
                               
        }
    }
    for(re int j=1;j<=m-k+1;++j)
    {
        front1=front2=back1=back2=q1[1]=q2[1]=1;
        for(re int i=2;i<=n;++i)
        {
            while(xmax[i][j]>=xmax[q1[back1]][j]&&front1<=back1) back1--;
            while(xmin[i][j]<=xmin[q2[back2]][j]&&front2<=back2) back2--;
            back1++,back2++;
            q1[back1]=i,q2[back2]=i;
            while(i-q1[front1]>=k) front1++;
            while(i-q2[front2]>=k) front2++;
            if(i>=k) ymax[i-k+1][j]=xmax[q1[front1]][j],ymin[i-k+1][j]=xmin[q2[front2]][j];
        }
    }
    
    for(re int i=1;i<=n-k+1;++i)
    {
        for(re int j=1;j<=m-k+1;++j)
        {
            ans=min(ans,ymax[i][j]-ymin[i][j]);
        }
    }
    printf("%d\n",ans);
    return 0;
}