Topic link: https://www.luogu.org/problem/P4782

 

Main idea of the title: There are n variables to satisfy m conditions.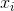For a or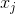For b, does the output exist to satisfy all conditions, and outputs

 

Topic train of thought: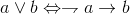So open 2*n points, the first n points are 0, and the last n points are 1, so that's it.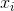Negative Proposition Direction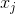Proposition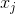Negative Proposition Direction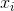Proposition, and then run a tarjan, if the proposition or not proposition in the same strong connected component, it does not exist, otherwise for each point, output belong small that.

 

The following is the code:

#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
#define ll long long
const int MAXN = 2e6+5;
int x,y,n,m,dfn[MAXN],low[MAXN],vis[MAXN],ans,tot,num,belong[MAXN],a,b;
vector<int>g[MAXN];
stack<int>s;
void tarjan(int u){
    low[u]=dfn[u]=++tot;
    s.push(u);
    vis[u]=1;
    int len=g[u].size();
    rep(i,0,len-1){
        int v=g[u][i];
        if(!dfn[v])tarjan(v),low[u]=min(low[u],low[v]);
        else if(vis[v])low[u]=min(low[u],dfn[v]);
    }
    if(low[u]==dfn[u]){
        num++;
        while(1){
            int now=s.top();
            s.pop();
            belong[now]=num;
            vis[now]=0;
            if(now==u)break;
        }
    }
}
int main(){
    while(~scanf("%d%d",&n,&m)){
        tot=0;
        ans=0;
        num=0;
        while(!s.empty())s.pop();
        memset(dfn,0,sizeof(dfn));
        memset(low,0,sizeof(low));
        memset(vis,0,sizeof(vis));
        memset(belong,0,sizeof(belong));
        rep(i,1,n)g[i].clear();
        rep(i,1,m){
            scanf("%d%d%d%d",&x,&a,&y,&b);
            int flag1=a^1,flag2=b^1;
            g[x+a*n].push_back(y+flag2*n);
            g[y+b*n].push_back(x+flag1*n);
        }
        rep(i,1,2*n){
            if(!dfn[i]){
                tarjan(i);
            }
        }
        int flag=0;
        rep(i,1,n){
            if(belong[i]==belong[i+n]){
                flag=1;
                break;
            }
        }
        if(flag)puts("IMPOSSIBLE");
        else{
            puts("POSSIBLE");
            rep(i,1,n){
                printf("%d%c",belong[i]<belong[i+n],i==n?'\n':' ');
            }
        }
    }
    return 0;
}