step by step
1. Introduction to the principle of kNN
2. Handwriting dataset test
3. Summary of advantages and disadvantages of the algorithm
1, Introduction to the principle of kNN
- 1.1 algorithm overview
- 1.2 example
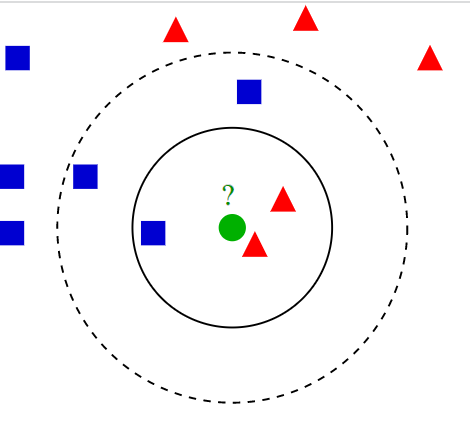
Note: the test sample (green circle) shall be classified as either the blue square of class I or the red triangle of class II. If k=3 (solid circle), it is assigned to the second category because there are 2 triangles and only 1 square within the inner circle. If k=5 (dotted circle), it is assigned to the first category (3 squares and 2 triangles within the outer circle).
- 1.3 algorithm Code Sample
import operator
def classify0(inX, dataSet, labels, k):
"""
parameter:
- inX: Input vector for classification
- dataSet: Input training sample set
- labels: Class label vector of sample data
- k: Used to select the number of nearest neighbors
"""
# Quantity of sample data obtained
dataSetSize = dataSet.shape[0]
# Matrix operation to calculate the difference between the test data and the corresponding data items of each sample data
diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet
# sqDistances sum of squares of the results of the previous step
sqDiffMat = diffMat**2
sqDistances = sqDiffMat.sum(axis=1)
# Take the square root to get the distance vector
distances = sqDistances**0.5
# Sort by distance from low to high
sortedDistIndicies = distances.argsort()
classCount = {}
# Take out the latest sample data in turn
for i in range(k):
# Record the category of the sample data
voteIlabel = labels[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
# Sort the frequency of categories from high to low
sortedClassCount = sorted(
classCount.items(), key=operator.itemgetter(1), reverse=True)
# Returns the most frequent category
return sortedClassCount[0][0]- 1.4 fast algorithm test
import numpy as np
# Create dataset
def createDataSet():
group = np.array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]])
labels = ['A', 'A', 'B', 'B']
return group, labels
group, labels = createDataSet()
print('group:', group)
print('labels:', labels) # Output value
# Test algorithm effect
classify0([0, 0], group, labels, 3)group: [[1. 1.1] [1. 1. ] [0. 0. ] [0. 0.1]] labels: ['A', 'A', 'B', 'B'] 'B'
2, Handwriting dataset test
- 2.1 downloading data sets
# Execute in the Jupiter notebook cell, download and unzip the data. !wget "http://labfile.oss.aliyuncs.com/courses/777/digits.zip" # decompression !unzip digits.zip
- 2.2 view the extracted text content 0_1.txt
!cat digits/testDigits/0_1.txt 00000000000000011000000000000000 00000000000111111110000000000000 00000000001111111111100000000000 00000000001111111111110000000000 00000000011111111111111000000000 00000000011111100011111000000000 00000000111110000001111000000000 00000000111110000001111100000000 00000000111110000000111110000000 00000001111110000000111110000000 00000001111110000000011111000000 00000001111110000000001111000000 00000001111110000000001111100000 00000001111100000000001111000000 00000001111000000000001111000000 00000001111000000000001111000000 00000001111000000000000111000000 00000000111100000000000111000000 00000000111100000000000111000000 00000000111100000000000111000000 00000001111000000000011110000000 00000001111000000000011110000000 00000000111000000000011110000000 00000000111110000011111110000000 00000000111110001111111100000000 00000000111111111111111000000000 00000000011111111111111000000000 00000000111111111111100000000000 00000000011111111111000000000000 00000000001111111000000000000000 00000000001111100000000000000000 00000000000100000000000000000000
- 2.3 image conversion to vector
# In order to use the classifier of the previous two examples, we must format the image into a vector. We will convert a 32x32 binary image matrix into a 1x1024 vector
def img2vector(filename):
# Create vector
returnVect = np.zeros((1, 1024))
# Open the data file and read the contents of each line
fr = open(filename)
for i in range(32):
# Read each line
lineStr = fr.readline()
# Convert the first 32 characters of each line into int and store it in the vector
for j in range(32):
returnVect[0, 32*i+j] = int(lineStr[j])
return returnVect
- 2.4 handwriting test
from os import listdir
def handwritingClassTest():
# List of class labels for sample data
hwLabels = []
# Sample data file list
trainingFileList = listdir('digits/trainingDigits')
trainingFileList = trainingFileList[1:]
m = len(trainingFileList)
# print(m)
# Initialize sample data matrix (M*1024)
trainingMat = np.zeros((m, 1024))
# Read all sample data to the data matrix in turn
for i in range(m):
# Extract the number in the file name
fileNameStr = trainingFileList[i]
# print(fileNameStr)
fileStr = fileNameStr.split('.')[0]
# print(fileStr)
# print((fileStr.split('_')[0]))
classNumStr = int((fileStr.split('_')[0]))
hwLabels.append(classNumStr)
# Store the sample data into the matrix
trainingMat[i, :] = img2vector(
'digits/trainingDigits/%s' % fileNameStr)
# Cycle read test data
testFileList = listdir('digits/testDigits')
testFileList = testFileList[1:]
# Initialization error rate
errorCount = 0.0
mTest = len(testFileList)
# Loop test each test data file
for i in range(mTest):
# Extract the number in the file name
fileNameStr = testFileList[i]
print(fileNameStr)
fileStr = fileNameStr.split('.')[0]
classNumStr = int(float((fileStr.split('_')[0])))
# Extract data vector
vectorUnderTest = img2vector('digits/testDigits/%s' % fileNameStr)
# Classify data files
classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3)
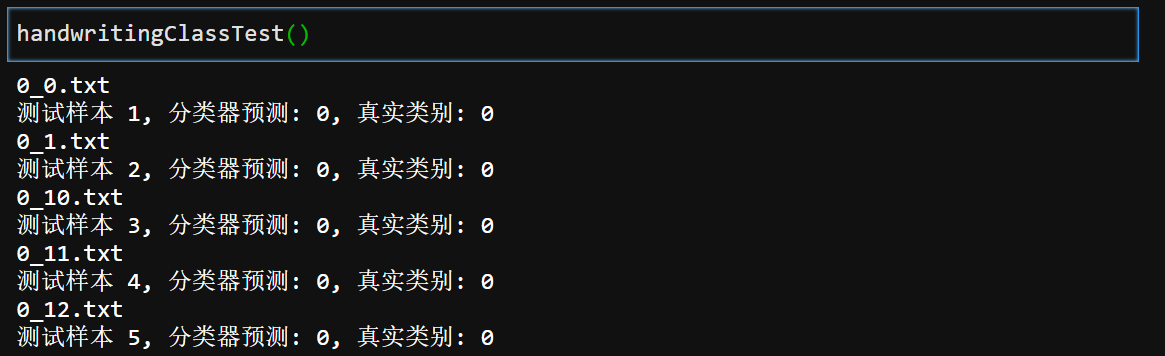
# Print the classification results of K-nearest neighbor algorithm and the real classification
print("Test sample %d, Classifier prediction: %d, Real category: %d" %
(i+1, classifierResult, classNumStr))
# Judge whether the result of K-nearest neighbor algorithm is accurate
if (classifierResult != classNumStr):
errorCount += 1.0
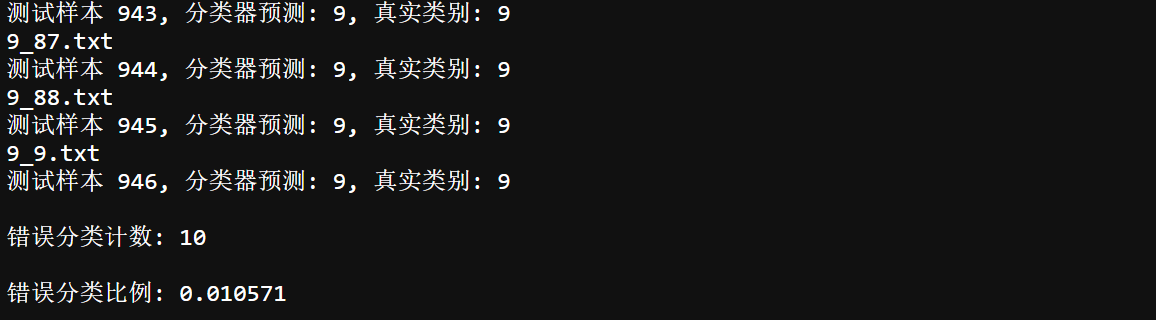
# Print error rate
print("\n Error classification count: %d" % errorCount)
print("\n Misclassification ratio: %f" % (errorCount/float(mTest)))
3, Summary of advantages and disadvantages of the algorithm
3.1 advantages
- 1. The principle of the algorithm is simple, easy to understand, high precision and mature theory. It can be used for both classification and regression;
- 2. It can adapt to many types of data;
- 3. It is especially suitable for multi-modal classification problems (objects have multiple category labels), and KNN performs better than SVM;
- 4. Compared with algorithms such as naive Bayes, it has no assumptions about data, high accuracy and insensitive to outliers.
3.2 disadvantages
- 1. The amount of calculation is too large, especially when the number of features is very large (for each text to be classified, the distance from it to all known samples must be calculated to obtain its K-th nearest neighbor);
- 2. When the samples are unbalanced, the prediction accuracy of rare categories is low (when the samples are unbalanced, for example, the sample size of one class is large and the sample size of other classes is small, which may lead to the majority of samples of large capacity in the K neighbors of the sample when a new sample is input);
- 3. The dependence on training data is very large, and the fault tolerance of training data is too poor (if one or two data in the training data set is wrong and just next to the value to be classified, it will directly lead to the inaccuracy of the predicted data)
- 4. Poor interpretability (unable to give the internal meaning of the data).