1. Single source shortest path without negative weight edge - Dijkstra
1.1 adjacency matrix version: applicable to the case where V does not exceed 1000, complexity o( 2 V 2 2V^2 2V2).
const int MAXV = 1000;
const int INF = 1000000000;
int n, G[MAXV][MAXV];
int d[MAXV];
bool vis[MAXV] = false;
void dijkstra(int s){
fill(d, d+MAXV, INF);
d[s] = 0;
for(int i=0; i<n; i++){
int u = -1, MIN = INF;
for(int j=0; j<n; j++){
if(!vis[j] && d[j] < MIN){
MIN = d[j];
u = j;
}
}
if(u == -1) return;
vis[u] = 1;
for(int v=0; v<n; v++){
if(!vis[v] && G[u][v] != INF){
if(d[v] > d[u] + G[u][v]){
d[v] = d[u] + G[u][v];
}
}
}
}
}
1.2 adjacency table version: complexity O( V 2 + E V^2 + E V2+E)
const int MAXV = 1000;
const int INF = 1000000000;
struct Node{
int v, dis; //v is the target vertex of the edge and dis is the edge weight.
};
vector<Node> Adj[MAXV];
int n;
int d[MAXV];
bool vis[MAXV] = false;
void dijkstra(int s){
fill(d, d+MAXV, INF);
d[s] = 0;
for(int i=0; i<n; i++){
int u = -1, MIN = INF;
for(int j=0; j<n; j++){
if(!vis[j] && d[j] < MIN){
MIN = d[j];
u = j;
}
}
if(u == -1) return;
vis[u] = 1;
//Only the following for loop is written differently from the adjacency matrix
for(int j=0; j<Adj[u].size(); j++){
int v = Adj[u][j].v;
if(!vis[v]){
if(d[v] > d[u] + Adj[u][j].dis){
d[v] = d[u] + Adj[u][j].dis;
}
}
}
}
}
1.3 Dijkstra for priority queue optimization
Optimization idea: priority can be used in the process of finding the smallest d[u]_ Queue to optimize the time, so that the final complexity can be reduced to o( V l o g V + E VlogV+E VlogV+E).
const int MAXV = 1000;
const int INF = 1000000000;
typedef pair<int,int> P; //first is the shortest distance and second is the number of vertices
struct Node{
int v, dis; //v is the target vertex of the edge and dis is the edge weight.
};
vector<Node> Adj[MAXV];
int n;
int d[MAXV];
bool vis[MAXV] = false;
void dijkstra(int s){
priority_queue<P, vector<P>, greater<P> > q;
fill(d, d+MAXV, INF);
d[s] = 0;
q.push(P(0,s));
while(!q.empty())
{
P p = q.top();
q.pop();
int u = p.second; //Number of vertices
if (d[u] < p.first) continue;
for(int j = 0; j < Adj[v].size(); j++)
{
int v = Adj[u][j].v;
if(!vis[v]){
if(d[v] > d[u] + Adj[u][j].dis){
d[v] = d[u] + Adj[u][j].dis;
q.push(P(d[v], v));
}
}
}
}
}
1.4 record the shortest path
Just add a pre array record precursor in the previous code:
int pre[MAXV];
if(!vis[v] && G[u][v] != INF){
if(d[v] > d[u] + G[u][v]){
d[v] = d[u] + G[u][v];
pre[v] = u;
}
}
After that, DFS traverses the reverse output:
void DFS(int s, int v){
if(v == s){
printf("%d\n",s);
return;
}
DFS(pre[v]);
printf("%d\n",s);
}
1.5 how to handle multiple rulers
1.5. 1. New edge weight
const int MAXV = 1000;
const int INF = 1000000000;
int cost[MAXV][MAXV]; //Cost is read from the topic and represents the cost between any two vertices
int c[MAXV]; //Except that the starting point is 0, others are initialized to INF
for(int v=0; v<n; v++){
if(!vis[v] && G[u][v] != INF){
if(d[v] > d[u] + G[u][v]){
d[v] = d[u] + G[u][v];
c[v] = c[u] + cost[u][v];
}
else if(d[v] == d[u] + G[u][v] && c[v] > c[u] + cost[u][v]){
c[v] = c[u] + cost[u][v];
}
}
}
1.5. 2. Add point weight
const int MAXV = 1000;
const int INF = 1000000000;
int weight[MAXV]; //Represents the weight of a vertex
int w[MAXV]; //Represents the maximum point weight that can be obtained from the starting point s to the vertex u. except that the starting point is weight[s], others are initialized to 0
for(int v=0; v<n; v++){
if(!vis[v] && G[u][v] != INF){
if(d[v] > d[u] + G[u][v]){
d[v] = d[u] + G[u][v];
w[v] = w[u] + weight[v];
}
else if(d[v] == d[u] + G[u][v] && w[v] > w[u] + weight[v]){
w[v] = w[u] + weight[v];
}
}
}
1.5. 3 find the number of shortest paths
const int MAXV = 1000;
const int INF = 1000000000;
int num[MAXV]; //Indicates the number of shortest paths from the starting point s to the vertex u. the starting point num[s] is initialized to 1 and the others are initialized to 0
for(int v=0; v<n; v++){
if(!vis[v] && G[u][v] != INF){
if(d[v] > d[u] + G[u][v]){
d[v] = d[u] + G[u][v];
num[v] = num[u];
}
else if(d[v] == d[u] + G[u][v]){
num[v] += num[u];
}
}
}
1.6 multiple scales and complex: Dijkstra + DFS
The situations given above are all related to "and", such as the sum of edge weights, the sum of point weights, the number of shortest paths, etc., but there may be some more complex methods for calculating edge weights or point weights, At this time, if you operate directly in Dijkstra algorithm, you may get wrong results (it may not meet the optimal substructure), so you can use a more general and templated method: first use Dijkstra algorithm to find all the shortest paths, and then use DFS to traverse each path, calculate the corresponding scale and select the optimal path.
1.6.1 Dijkstra dictation template
const int MAXV = 1000;
const int INF = 1000000000;
int n, G[MAXV][MAXV];
int d[MAXV];
vector<int> pre[MAXV];
bool vis[MAXV] = false;
void dijkstra(int s){
fill(d, d+MAXV, INF);
d[s] = 0;
for(int i=0; i<n; i++){
int u = -1, MIN = INF;
for(int j=0; j<n; j++){
if(!vis[j] && d[j] < MIN){
MIN = d[j];
u = j;
}
}
if(u == -1) return;
vis[u] = 1;
for(int v=0; v<n; v++){
if(!vis[v] && G[u][v] != INF){
if(d[v] > d[u] + G[u][v]){
d[v] = d[u] + G[u][v];
pre[v].clear();
pre[v].push_back(u);
}
else if(d[v] == d[u] + G[u][v]){
pre[v].push_back(u);
}
}
}
}
}
1.6.2 DFS traverses all shortest path templates
It should be noted that the paths stored in the path are in reverse order, so the access nodes need to be reversed.
int optvalue;
vector<int> pre[MAXV];
vector<int> path, tempPath;
int pathnum = 0; //Record the number of shortest paths
void DFS(int v){
if(v == st){
tempPath.push_back(st);
int value;
Calculation path tempPath Upper value value;
if(value > optvalue){
optvalue = value;
path = tempPath;
}
pathnum++;
tempPath.pop_back();
return;
}
tempPath.push_back(v);
for(int i=0; i<pre[v].size; i++){
DFS(pre[v][i]);
}
tempPath.pop_back();
}
2 single source shortest path with negative weight edge -- Bellman Ford algorithm and SPFA algorithm
2.1 BF algorithm, complexity O ( V E ) O(VE) O(VE).
The idea of the algorithm is to perform n-1 rounds of operations on the edges in the graph. Each round traverses all the edges in the graph and relaxes each edge. If there is no negative ring reachable by the source point, all values in Array d should be optimal after n-1 round of operation. At this time, traverse all edges again. If it can be relaxed, it indicates that the active point can reach the negative ring. If the collar matrix is used in BF algorithm, the complexity will rise to O ( V 2 ) O(V^2) O(V2).
for(int i=0; i<n-1; i++){
int flag = 0;
for(each edge u->v){
if(d[u] + length[u->v] < d[v]){
d[v] = d[u] + length[u->v];
flag = 1;
}
}
if(flag == 0) break; //If you find that all edges have no double relaxation during a round of operation, exit directly.
}
//false if there is a negative ring reachable to the origin.
for(each edge u->v){
if(d[u] + length[u->v] < d[v]){
return false;
}
}
As for the solution of the shortest path, the method of multiple scales is the same as Dijkstra. The only thing to pay attention to is the method of counting the shortest path. Since the nodes that have been visited will be accessed many times during the BF algorithm, if the method in Dijkstra is followed, repeated statistics will be caused. It is necessary to set the set pre[MAXV] of the record precursor. When a path with the same length as the existing shortest path is encountered, To set num[v] to 0, traverse the precursors saved in set and count again.
const int MAXV = 1000;
const int INF = 1000000000;
struct Node{
int v, dis; //v is the target vertex of the edge and dis is the edge weight.
};
vector<Node> Adj[MAXV];
int n;
int d[MAXV], num[MAXV];
set<int> pre[MAXV];
void BF(int s){
fill(d, d+MAXV, INF);
fill(num, num+MAXV, 0);
num[s] = 1;
d[s] = 0;
for(int i=0; i<n-1; i++){
for(int u=0; u<n; u++){
for(int j=0; j<Adj[u].size(); j++){
int v = Adj[u][j].v;
int dis = Adj[u][j].dis;
if(d[u] + dis < d[v]){
d[v] = d[u] + dis;
num[v] = num[u];
pre[v].clear();
pre[v].insert(u);
}
else if(d[u] + dis == d[v]){
pre[v].insert(u); // Re count num[v]
num[v] = 0;
for(auto it = pre[v].begin(); it != pre[v].end(); it++){
num[v] += num[*it];
}
}
}
}
}
}
2.2 SPFA algorithm, complexity O ( k E ) O(kE) O(kE).
Note that only when the d[u] value of a vertex u changes, the d[v] value of the adjacency point v of the edge starting from it may change. Therefore, a queue can be established, the first node U of the queue can be taken out each time, and then all adjacent edges u - > V starting from u can be relaxed. If the relaxation is successful, if the V at this time is not in the queue, it will be added to the queue. Do this until the queue is empty (indicating that there is no negative ring reachable from the source point in the graph), or the queue number of a vertex exceeds V-1 (indicating that there is a negative ring reachable from the source point in the graph). If it is known that there is no reachable negative ring in the graph, the innum array can be omitted.
If the negative ring is not reachable from the source point, you need to add an auxiliary vertex C, a directed edge from the source point to C, and V-1 directed edges from C to other vertices except the source point. This makes the originally unreachable negative ring reachable.
const int MAXV = 1000;
const int INF = 1000000000;
struct Node{
int v, dis; //v is the target vertex of the edge and dis is the edge weight.
};
vector<Node> Adj[MAXV];
int n;
int d[MAXV], innum[MAXV]; //Record the number of times you join the team
bool inq[MAXV]; //Is the vertex in the queue
void SPFA(int s){
fill(d, d+MAXV, INF);
fill(innum, innum+MAXV, 0);
fill(inq, inq+MAXV, 0);
queue<int> q;
q.push(s);
inq[s] = 1;
innum[s]++;
d[s] = 0;
while(!q.empty()){
int u = q.front();
q.pop();
inq[u] = false;
for(int j=0; j<Adj[u].size(); j++){
int v = Adj[u][j].v;
int dis = Adj[u][j].dis;
if(d[u] + dis < d[v]){
d[v] = d[u] + dis;
if(!inq[v]){
q.push(v);
inq[v] = 1;
innum[v]++;
if(innum[v] >= n) return false; //Reachable negative ring
}
}
}
}
return true; //No reachable negative ring
}
The above is the BFS version of SPFA. If we find a relaxed edge, the next operation is not to add it to the queue, but to continue to relax directly along this edge, this is the DFS version of SPFA. The DFS version of SPFA has a miraculous effect on ring judgment. * * the ring judgment basis of DFS version of SPFA: if a node occurs twice or more, there is a negative ring** The following code only judges the negative ring, so you can initialize the d[MAXV] array to 0.
const int MAXV = 1000;
const int INF = 1000000000;
struct Node{
int v, dis; //v is the target vertex of the edge and dis is the edge weight.
};
vector<Node> Adj[MAXV];
int n;
int d[MAXV];
bool vis[MAXV]; //Has the storage node ever appeared
int flag = 0; //Negative Ring found
void DFS_SPFA(int u){
fill(d, d+MAXV, 0);
vis[u] = 1;
for(int i=0; i<Adj[u].size(); i++){
int v = Adj[u][j].v;
int dis = Adj[u][j].dis;
if(d[u] + dis < d[v]){
if(vis[v] || flag){
flag = 1;
break;
}
d[v] = d[u] + dis;
DFS_SPFA(v);
}
}
vis[u] = 0;
}
void main(){
//Each vertex judges a negative ring
for(int i=0; i<n; i++){
DFS_SPFA(i);
if(flag) break;
}
}
3 all source shortest path -- Floyd algorithm
All source shortest path problem: for a given graph G, find the shortest path length between any two points. The time complexity is O ( n 3 ) O(n^3) O(n3), so the number of vertices n is limited to 200, and it is very suitable to use Floyd algorithm to store graphs using adjacency matrix.
The idea of Floyd algorithm is very concise: if there is vertex K, which shortens the current shortest distance between vertex i and vertex j when k is used as the intermediary point, vertex K is used as the intermediary point between vertex i and vertex j. The core code is as follows:
void Floyd(){
for(int k=0; k<n; k++){
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
if(dis[i][k] != INF && dis[k][j] != INF && dis[i][k] + dis[k][j] < dis[i][j]){
dis[i][j] = dis[i][k] + dis[k][j];
}
}
}
}
}
int main(){
fill(dis[0], dis[0]+MAXV*MAXV, INF);
for(int i=0; i<n; i++){
dis[i][i] = 0; //The distance from each vertex to itself is initialized to 0
}
cin >> u >> v >> w;
dis[u][v] = w; //Enter the distance from u to v as w
Floyd(); //Call Floyd() algorithm
output dis Array.
}
4 example analysis
4.1 A1003 Emergency (25 points)
Template problem, find the number of shortest paths and the maximum point weight sum.
4.1. 1 conventional Dijkstra
//Regular Dijkstra
#include<bits/stdc++.h>
using namespace std;
const int MAXV = 505;
const int INF = 1000000000;
int n, m, c1, c2;
int weight[MAXV];
int G[MAXV][MAXV];
int pathnum[MAXV], w[MAXV], d[MAXV];
bool vis[MAXV];
void Dijkstra(int s){
fill(d, d+MAXV, INF);
pathnum[s] = 1;
w[s] = weight[s];
d[s] = 0;
for(int i=0; i<n; i++){
int u = -1, MIN = INF;
for(int j=0; j<n; j++){
if(!vis[j] && d[j] < MIN){
MIN = d[j];
u = j;
}
}
if(u == -1) return;
vis[u] = 1;
for(int v=0; v<n; v++){
if(!vis[v] && G[u][v] != INF){
if(G[u][v] + d[u] < d[v]){
d[v] = G[u][v] + d[u];
pathnum[v] = pathnum[u];
w[v] = w[u] + weight[v];
}
else if(G[u][v] + d[u] == d[v]){
pathnum[v] += pathnum[u];
if(w[v] < w[u] + weight[v]){
w[v] = w[u] + weight[v];
}
}
}
}
}
return;
}
int main(){
fill(G[0], G[0]+MAXV*MAXV, INF);
int a, b, len;
cin >> n >> m >> c1 >> c2;
for(int i=0; i<n; i++){
scanf("%d",&weight[i]);
}
for(int i=0; i<m; i++){
scanf("%d %d %d",&a, &b, &len);
G[a][b] = G[b][a] = len;
}
Dijkstra(c1);
printf("%d %d",pathnum[c2], w[c2]);
}
4.1. 2 Dijkstra for priority queue optimization
//Dijkstra for priority queue optimization
#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> p;
const int MAXV = 505;
const int INF = 1000000000;
int n, m, c1, c2;
int weight[MAXV];
int G[MAXV][MAXV];
int pathnum[MAXV], w[MAXV], d[MAXV];
bool vis[MAXV];
void Dijkstra(int s){
fill(d, d+MAXV, INF);
pathnum[s] = 1;
w[s] = weight[s];
d[s] = 0;
priority_queue<p, vector<p>, greater<p> > q;
q.push(p(0,s));
while(!q.empty()){
int u = q.top().second;
q.pop();
vis[u] = 1;
for(int v=0; v<n; v++){
if(!vis[v] && G[u][v] != INF){
if(G[u][v] + d[u] < d[v]){
d[v] = G[u][v] + d[u];
pathnum[v] = pathnum[u];
w[v] = w[u] + weight[v];
q.push(p(d[v],v));
}
else if(G[u][v] + d[u] == d[v]){
pathnum[v] += pathnum[u];
if(w[v] < w[u] + weight[v]){
w[v] = w[u] + weight[v];
}
}
}
}
}
return;
}
int main(){
fill(G[0], G[0]+MAXV*MAXV, INF);
int a, b, len;
cin >> n >> m >> c1 >> c2;
for(int i=0; i<n; i++){
scanf("%d",&weight[i]);
}
for(int i=0; i<m; i++){
scanf("%d %d %d",&a, &b, &len);
G[a][b] = G[b][a] = len;
}
Dijkstra(c1);
printf("%d %d",pathnum[c2], w[c2]);
}
4.1.3 DFS + Dijkstra
//DFS + Dijkstra
#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> p;
const int MAXV = 505;
const int INF = 1000000000;
int n, m, c1, c2;
int weight[MAXV];
int G[MAXV][MAXV];
int d[MAXV];
bool vis[MAXV];
int pathnum = 0, maxWeight = -1;
vector<int> tempPath, ansPath;
vector<int> pre[MAXV]; //Record node precursor
void Dijkstra(int s){
fill(d, d+MAXV, INF);
d[s] = 0;
priority_queue<p, vector<p>, greater<p> > q;
q.push(p(0,s));
while(!q.empty()){
int u = q.top().second;
q.pop();
vis[u] = 1;
for(int v=0; v<n; v++){
if(!vis[v] && G[u][v] != INF){
if(G[u][v] + d[u] < d[v]){
d[v] = G[u][v] + d[u];
pre[v].clear();
pre[v].push_back(u);
q.push(p(d[v],v));
}
else if(G[u][v] + d[u] == d[v]){
pre[v].push_back(u);
}
}
}
}
return;
}
void DFS(int v){
if(v == c1){
tempPath.push_back(v);
pathnum++;
int tempVal = 0;
for(int j=tempPath.size()-1; j>=0; j--){
tempVal += weight[tempPath[j]];
}
if(tempVal > maxWeight){
maxWeight = tempVal;
ansPath = tempPath;
}
tempPath.pop_back();
return;
}
else{
tempPath.push_back(v);
for(int i=0; i<pre[v].size(); i++){
DFS(pre[v][i]);
}
tempPath.pop_back();
}
return;
}
int main(){
fill(G[0], G[0]+MAXV*MAXV, INF);
int a, b, len;
cin >> n >> m >> c1 >> c2;
for(int i=0; i<n; i++){
scanf("%d",&weight[i]);
}
for(int i=0; i<m; i++){
scanf("%d %d %d",&a, &b, &len);
G[a][b] = G[b][a] = len;
}
Dijkstra(c1);
DFS(c2);
printf("%d %d",pathnum, maxWeight);
}
4.1.4 SPFA
//SPFA
#include<bits/stdc++.h>
using namespace std;
const int MAXV = 505;
const int INF = 1000000000;
struct Node{
int v, dis;
};
int n, m, c1, c2;
int weight[MAXV];
vector<Node> Adj[MAXV];
unordered_set<int> pre[MAXV];
int d[MAXV];
bool inq[MAXV];
int pathnum[MAXV], w[MAXV];
void SPFA(int s){
fill(d, d+MAXV, INF);
d[s] = 0;
pathnum[s] = 1;
w[s] = weight[s];
queue<int> q;
q.push(s);
inq[s] = 1;
while(!q.empty()){
int u = q.front();
q.pop();
inq[u] = 0;
for(int i=0; i<Adj[u].size(); i++){
int v = Adj[u][i].v;
int dis = Adj[u][i].dis;
if(d[u] + dis < d[v]){
d[v] = d[u] + dis;
pre[v].clear();
pre[v].insert(u);
pathnum[v] = pathnum[u];
w[v] = w[u] + weight[v];
if(!inq[v]){
q.push(v);
inq[v] = 1;
}
}
else if(d[u] + dis == d[v]){
pre[v].insert(u);
pathnum[v] = 0;
for(auto it = pre[v].begin(); it != pre[v].end(); it++){
pathnum[v] += pathnum[*it];
}
if(w[v] < w[u] + weight[v]){
w[v] = w[u] + weight[v];
}
if(!inq[v]){
q.push(v);
inq[v] = 1;
}
}
}
}
return;
}
int main(){
int a, b, len;
cin >> n >> m >> c1 >> c2;
for(int i=0; i<n; i++){
scanf("%d",&weight[i]);
}
for(int i=0; i<m; i++){
scanf("%d %d %d",&a, &b, &len);
Adj[a].push_back({b,len});
Adj[b].push_back({a,len});
}
SPFA(c1);
printf("%d %d",pathnum[c2], w[c2]);
}
4.2 A1018 Public Bike Management (30 points)
The process of calculating the second scale of this problem is complex, and there is a risk of not meeting the optimal substructure, so Dijkstra+DFS is directly selected to solve it.
//DFS + Dijkstra
#include<bits/stdc++.h>
using namespace std;
const int MAXV = 505;
const int INF = 1000000000;
int bikeNum[MAXV], d[MAXV];
int G[MAXV][MAXV];
bool vis[MAXV];
vector<int> pre[MAXV];
vector<int> tempPath, ansPath;
int minTakeBack = INF, minSend = INF;
int cmax, n, sp, m;
void Dijkstra(int s){
fill(d, d+MAXV, INF);
d[s] = 0;
for(int i=0; i<n+1; i++){
int u = -1, MIN = INF;
for(int j=0; j<n+1; j++){
if(!vis[j] && d[j] < MIN){
MIN = d[j];
u = j;
}
}
if(u == -1) return;
vis[u] = 1;
for(int v=0; v<n+1; v++){
if(!vis[v] && G[u][v] != INF){
if(d[u] + G[u][v] < d[v]){
d[v] = d[u] + G[u][v];
pre[v].clear();
pre[v].push_back(u);
}
else if(d[u] + G[u][v] == d[v]){
pre[v].push_back(u);
}
}
}
}
return;
}
void DFS(int v){
if(v == 0){
tempPath.push_back(0);
int take = 0, send = 0, capacity = cmax / 2;
int carry = 0;
for(int i=tempPath.size()-2; i>=0; i--){
if(carry + bikeNum[tempPath[i]] - capacity < 0){
send += capacity - bikeNum[tempPath[i]] - carry;
carry = 0;
}
else if(carry + bikeNum[tempPath[i]] - capacity == 0) carry = 0;
else{
carry = carry + bikeNum[tempPath[i]] - capacity;
}
}
take = carry;
if(send < minSend || send == minSend && take < minTakeBack){
minTakeBack = take;
minSend = send;
ansPath = tempPath;
}
tempPath.pop_back();
}
else{
tempPath.push_back(v);
for(int i=0; i<pre[v].size(); i++){
DFS(pre[v][i]);
}
tempPath.pop_back();
}
return;
}
int main(){
int a, b, len;
fill(G[0], G[0]+MAXV*MAXV, INF);
cin >> cmax >> n >> sp >> m;
for(int i=1; i<=n; i++){
scanf("%d",&bikeNum[i]);
}
for(int i=0; i<m; i++){
scanf("%d %d %d",&a, &b, &len);
G[a][b] = G[b][a] = len;
}
Dijkstra(0);
DFS(sp);
printf("%d ",minSend);
for(int j=ansPath.size()-1; j>=0; j--){
printf("%d",ansPath[j]);
if(j > 0) printf("->");
}
printf(" %d",minTakeBack);
}
4.3 A1030 Travel Plan (30 points)
The second ruler is the edge weight, which conforms to the optimal substructure and can be solved directly by Dijkstra.
#include<bits/stdc++.h>
using namespace std;
const int MAXV = 505;
const int INF = 1000000000;
int n, m, s, ed;
int G[MAXV][MAXV], C[MAXV][MAXV];
int d[MAXV], c[MAXV];
bool vis[MAXV];
int pre[MAXV];
void Dijkstra(int s){
fill(d, d+MAXV, INF);
d[s] = 0;
c[s] = 0;
for(int i=0; i<n; i++){
int u = -1, MIN = INF;
for(int j=0; j<n; j++){
if(!vis[j] && d[j] < MIN){
MIN = d[j];
u = j;
}
}
if(u == -1) return;
vis[u] = 1;
for(int v=0; v<n; v++){
if(!vis[v] && G[u][v] != INF){
if(G[u][v] + d[u] < d[v] || G[u][v] + d[u] == d[v] && c[v] > C[u][v] + c[u]){
d[v] = G[u][v] + d[u];
c[v] = C[u][v] + c[u];
pre[v] = u;
}
}
}
}
return;
}
void DFS(int v){
if(v == s){
printf("%d ",s);
return;
}
DFS(pre[v]);
printf("%d ",v);
}
int main(){
int a,b,dis,cost;
fill(G[0], G[0]+MAXV*MAXV, INF);
fill(C[0], C[0]+MAXV*MAXV, INF);
cin >> n >> m >> s >> ed;
for(int i=0; i<m; i++){
scanf("%d %d %d %d",&a,&b,&dis,&cost);
G[a][b] = G[b][a] = dis;
C[a][b] = C[b][a] = cost;
}
Dijkstra(s);
DFS(ed);
printf("%d %d",d[ed],c[ed]);
}
4.4 A1072 Gas Station (30 points)
To calculate multiple shortest paths, you can still use conventional Dijkstra. It should be noted that stoi() should be used for subscript conversion. str[1] - '0' cannot be used because G10 appears!!
#include<bits/stdc++.h>
using namespace std;
const int MAXV = 1020;
const int INF = 1000000000;
int n, m, k, ds;
int G[MAXV][MAXV];
int d[MAXV];
bool vis[MAXV];
int ansdis = -1, anssum = INF, ansIdx = -1;
void Dijkstra(int s){
fill(d, d+MAXV, INF);
fill(vis, vis+MAXV, false);
d[s] = 0;
for(int i=0; i<n+m; i++){
int u = -1, MIN = INF;
for(int j=1; j<=n+m; j++){
if(!vis[j] && d[j] < MIN){
MIN = d[j];
u = j;
}
}
if(u == -1) return;
vis[u] = 1;
for(int v=1; v<=n+m; v++){
if(!vis[v] && G[u][v] + d[u] < d[v]){
d[v] = G[u][v] + d[u];
}
}
}
return;
}
int main(){
fill(G[0], G[0]+MAXV*MAXV, INF);
string stra, strb;
bool flag = false;
int dis, a, b;
cin >> n >> m >> k >> ds;
for(int i=0; i<k; i++){
cin >> stra >> strb >> dis;
if(stra[0] == 'G') a = n + stoi(stra.substr(1));
else a = stoi(stra);
if(strb[0] == 'G') b = n + stoi(strb.substr(1));
else b = stoi(strb);
G[a][b] = G[b][a] = dis;
}
for(int i=n+1; i<=n+m; i++){
Dijkstra(i);
int j = 1, mindis = INF, sum = 0;
for(; j<=n; j++){
if(d[j] > ds) break;
if(d[j] < mindis) mindis = d[j];
sum += d[j];
}
if(j == n+1){
flag = true;
if(mindis > ansdis || mindis == ansdis && sum < anssum){
ansdis = mindis;
anssum = sum;
ansIdx = i;
}
}
}
double ans1, ans2;
ans1 = ansdis;
ans2 = (double)anssum / (double)n;
if(anssum == INF) printf("No Solution\n");
else{
printf("G%d\n",ansIdx-n);
printf("%.1f %.1f\n", ans1, ans2);
}
}
4.5 A1087 All Roads Lead to Rome (30 points)
Because there is a condition with the highest average happiness value, it may not meet the optimal substructure, so Dijkstra+DFS directly solves:
#include<bits/stdc++.h>
using namespace std;
const int MAXV = 205;
const int INF = 1000000000;
int n, m;
int G[MAXV][MAXV];
unordered_map<string, int> cityToIdx;
unordered_map<int, string> idxToCity;
int cityHappy[MAXV], d[MAXV];
vector<int> pre[MAXV];
vector<int> tempPath, ansPath;
int idx = 1;
bool vis[MAXV];
int ansnum = 0, maxHappy = -1, maxAver = -1;
void Dijkstra(int s){
fill(d, d+MAXV, INF);
d[s] = 0;
for(int i=0; i<n; i++){
int u = -1, MIN = INF;
for(int j=0; j<n; j++){
if(!vis[j] && d[j] < MIN){
MIN = d[j];
u = j;
}
}
if(u == -1) return;
vis[u] = 1;
for(int v=0; v<n; v++){
if(!vis[v] && G[u][v] != INF){
if(G[u][v] + d[u] < d[v]){
d[v] = G[u][v] + d[u];
pre[v].clear();
pre[v].push_back(u);
}
else if(G[u][v] + d[u] == d[v]){
pre[v].push_back(u);
}
}
}
}
return;
}
void DFS(int v){
if(v == 0){
ansnum++;
tempPath.push_back(0);
int nowhappy = 0, nowaver = 0;
for(int j=tempPath.size()-2; j>=0; j--){
nowhappy += cityHappy[tempPath[j]];
}
nowaver = nowhappy / (tempPath.size()-1);
if(nowhappy > maxHappy || nowhappy == maxHappy && nowaver > maxAver){
maxHappy = nowhappy;
maxAver = nowaver;
ansPath = tempPath;
}
tempPath.pop_back();
return;
}
else{
tempPath.push_back(v);
for(int i=0; i<pre[v].size(); i++){
DFS(pre[v][i]);
}
tempPath.pop_back();
}
return;
}
int main(){
fill(G[0], G[0]+MAXV*MAXV, INF);
string city, tarcity;
int happy, cost;
cin >> n >> m >> city;
cityToIdx[city] = 0;
idxToCity[0] = city;
for(int i=1; i<n; i++){
cin >> city >> happy;
if(cityToIdx[city] == 0){
cityToIdx[city] = idx;
idxToCity[idx] = city;
idx++;
}
cityHappy[cityToIdx[city]] = happy;
}
for(int i=1; i<=m; i++){
cin >> city >> tarcity >> cost;
int a = cityToIdx[city];
int b = cityToIdx[tarcity];
G[a][b] = G[b][a] = cost;
}
Dijkstra(0);
DFS(cityToIdx["ROM"]);
printf("%d %d %d %d\n",ansnum, d[cityToIdx["ROM"]], maxHappy, maxAver);
for(int i=ansPath.size()-1; i>0; i--){
printf("%s->", idxToCity[ansPath[i]].c_str());
}
printf("ROM");
}
4.6 A1111 Online Map (30 points)
Two dijkstras need to be used for this problem, and the corresponding shortest path is saved for comparison output:
#include<bits/stdc++.h>
using namespace std;
const int INF = 1000000000;
int n, m;
struct Node{
int v, len, tim;
Node(int a, int b, int c){
v = a;
len = b;
tim = c;
}
};
vector<Node> G[505];
int st, ed;
bool visit[505] = {0};
int d[505] = {0};
int cost[505] = {0};
int pre_d[505], pre_t[505];
int internum[505] = {0};
string ans_t, ans_d;
void Dijkstra_d(int s){
fill(d, d+505, INF);
fill(cost, cost+505, INF);
fill(pre_d, pre_d+505, -1);
d[s] = 0;
cost[s] = 0;
for(int i=0; i<n; i++){
int x = -1, MIN = INF;
for(int j=0; j<n; j++){
if(!visit[j] && d[j] != INF){
if(d[j] < MIN){
MIN = d[j];
x = j;
}
}
}
if(x == -1) return;
visit[x] = 1;
for(int j=0; j<G[x].size(); j++){
Node neighber = G[x][j];
if(!visit[neighber.v]){
if(d[neighber.v] > d[x] + neighber.len || (d[neighber.v] == d[x] + neighber.len && cost[neighber.v] > cost[x] + neighber.tim)){
d[neighber.v] = d[x] + neighber.len;
cost[neighber.v] = cost[x] + neighber.tim;
pre_d[neighber.v] = x;
}
}
}
}
}
void DFS_d(int st, int ed, int acl_ed){
if(ed == st){
ans_d += to_string(st) + " -> ";
return;
}
if(ed >= 0)
DFS_d(st, pre_d[ed], acl_ed);
if(ed != acl_ed) ans_d += to_string(ed) + " -> ";
else ans_d += to_string(ed);
}
void DFS_t(int st, int ed, int acl_ed){
if(ed == st){
ans_t += to_string(st) + " -> ";
return;
}
if(ed >= 0)
DFS_t(st, pre_t[ed], acl_ed);
if(ed != acl_ed) ans_t += to_string(ed) + " -> ";
else ans_t += to_string(ed);
}
void Dijkstra_t(int s){
fill(visit, visit+505, 0);
fill(cost, cost+505, INF);
fill(pre_t, pre_t+505, -1);
cost[s] = 0;
for(int i=0; i<n; i++){
int x = -1, MIN = INF;
for(int j=0; j<n; j++){
if(!visit[j] && cost[j] != INF){
if(cost[j] < MIN){
MIN = cost[j];
x = j;
}
}
}
if(x == -1) return;
visit[x] = 1;
for(int j=0; j<G[x].size(); j++){
Node neighber = G[x][j];
if(!visit[neighber.v]){
if(cost[neighber.v] > cost[x] + neighber.tim || (cost[neighber.v] == cost[x] + neighber.tim && internum[neighber.v] > internum[x] + 1)){
cost[neighber.v] = cost[x] + neighber.tim;
internum[neighber.v] = internum[x] + 1;
pre_t[neighber.v] = x;
}
}
}
}
}
int main(){
int v1, v2, oneway, t, length;
scanf("%d %d",&n,&m);
for(int i=0; i<m; i++){
scanf("%d %d %d %d %d",&v1,&v2,&oneway,&length,&t);
G[v1].push_back(Node(v2,length,t));
if(oneway != 1) G[v2].push_back(Node(v1,length,t));
}
scanf("%d %d",&st,&ed);
Dijkstra_d(st);
Dijkstra_t(st);
DFS_d(st, ed, ed);
DFS_t(st, ed, ed);
if(ans_d == ans_t) printf("Distance = %d; Time = %d: %s",d[ed],cost[ed],ans_t.c_str());
else{
printf("Distance = %d: %s\n",d[ed], ans_d.c_str());
printf("Time = %d: %s\n",cost[ed], ans_t.c_str());
}
}
4.7 A1131 Subway Map (30 points)
"dijkstra is an upgraded version of bfs, which means that if the shortest path is found, bfs is no longer applicable when the graph changes from an unauthorized value to a weighted value, so we use the dijkstra method. In other words, for an unauthorized value graph, the dijkstra method is the same as bfs. You can draw an unauthorized graph, walk through it with dijkstra, and find that this is actually bfs."
A small trick of this problem is to open the line when storing the number of lines the path between any two stations belongs to [ 10000 ] [ 10000 ] [10000][10000] The array of [10000] [10000] will exceed the memory limit (actual test int) x [ 23000 ] [ 23000 ] x[23000][23000] x[23000][23000]= {0} is the limit of 64M memory requirements). Consider taking the previous platform as the high four bits and the latter as the low four bits, and use unordered_ Map < int, int > is stored, that is, line[stop[0] * 10000 + stop[1]] = 1;
// DFS + Dijkstra + priority queue optimization
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 10005;
const int INF = 1000000000;
typedef pair<int, int> p;
vector<int> G[MAXN];
unordered_map<int, int> line;
unordered_set<int> stops;
vector<int> pre[MAXN];
vector<int> tempPath, ansPath, ansTstop, ansLine;
int n, m, k, st, ed;
int minTransfer = INF;
int d[MAXN];
bool vis[MAXN];
void Dijkstra(int s){
fill(d, d+MAXN, INF);
fill(vis, vis+MAXN, false);
priority_queue<p, vector<p>, greater<p> > q;
q.push(p(0,s));
d[s] = 0;
int stopnum = stops.size();
while(!q.empty()){
p tempP = q.top();
q.pop();
int u = tempP.second;
// int u = -1, MIN = INF;
// for(auto it = stops.begin(); it != stops.end(); it++){
// int j = *it;
// if(!vis[j] && d[j] < MIN){
// MIN = d[j];
// u = j;
// }
// }
// if(u == -1) return;
vis[u] = 1;
for(int j=0; j<G[u].size(); j++){
int v = G[u][j];
if(!vis[v]){
if(d[u] + 1 < d[v]){
d[v] = d[u] + 1;
pre[v].clear();
pre[v].push_back(u);
q.push(p(d[v], v));
}
else if(d[u] + 1 == d[v]){
pre[v].push_back(u);
q.push(p(d[v], v));
}
}
}
}
return;
}
void DFS(int v){
if(v == st){
tempPath.push_back(st);
int tempTransfer = 0;
vector<int> tempTstop, tempLine;
if(tempPath.size() >= 3){
int j = tempPath.size() - 1;
int preline = line[tempPath[j]*10000 + tempPath[j-1]];
for(j=tempPath.size()-3; j>=0; j--){
int nowline = line[tempPath[j]*10000 + tempPath[j+1]];
if(preline != nowline){
tempTransfer++;
tempTstop.push_back(tempPath[j+1]);
tempLine.push_back(nowline);
}
preline = nowline;
}
}
if(tempTransfer < minTransfer){
minTransfer = tempTransfer;
ansPath = tempPath;
ansTstop = tempTstop;
ansLine = tempLine;
}
tempPath.pop_back();
}
else{
tempPath.push_back(v);
for(int i=0; i<pre[v].size(); i++){
DFS(pre[v][i]);
}
tempPath.pop_back();
}
return;
}
int main(){
scanf("%d",&n);
for(int i=1; i<=n; i++){
int last, temp;
scanf("%d %d",&m,&last);
stops.insert(last);
for(int j=1; j<m; j++){
scanf("%d",&temp);
stops.insert(temp);
G[last].push_back(temp);
G[temp].push_back(last);
line[last*10000 + temp] = line[temp*10000 + last] = i;
last = temp;
}
}
scanf("%d",&k);
for(int i=0; i<k; i++){
scanf("%d %d",&st,&ed);
tempPath.clear();
minTransfer = INF;
Dijkstra(st);
DFS(ed);
printf("%d\n",d[ed]);
int startLine = line[st * 10000 + ansPath[ansPath.size()-2]];
if(ansTstop.size() == 0) printf("Take Line#%d from %04d to %04d.\n",startLine, st, ed);
else{
printf("Take Line#%d from %04d to %04d.\n",startLine, st, ansTstop[0]);
int j = 1;
for(; j<ansTstop.size(); j++){
printf("Take Line#%d from %04d to %04d.\n", ansLine[j-1], ansTstop[j-1], ansTstop[j]);
}
printf("Take Line#%d from %04d to %04d.\n",ansLine[j-1], ansTstop[j-1], ed);
}
}
}
4.8 2021 spring PAT grade a real topic T4 Recycling of Shared Bicycles (30 points)
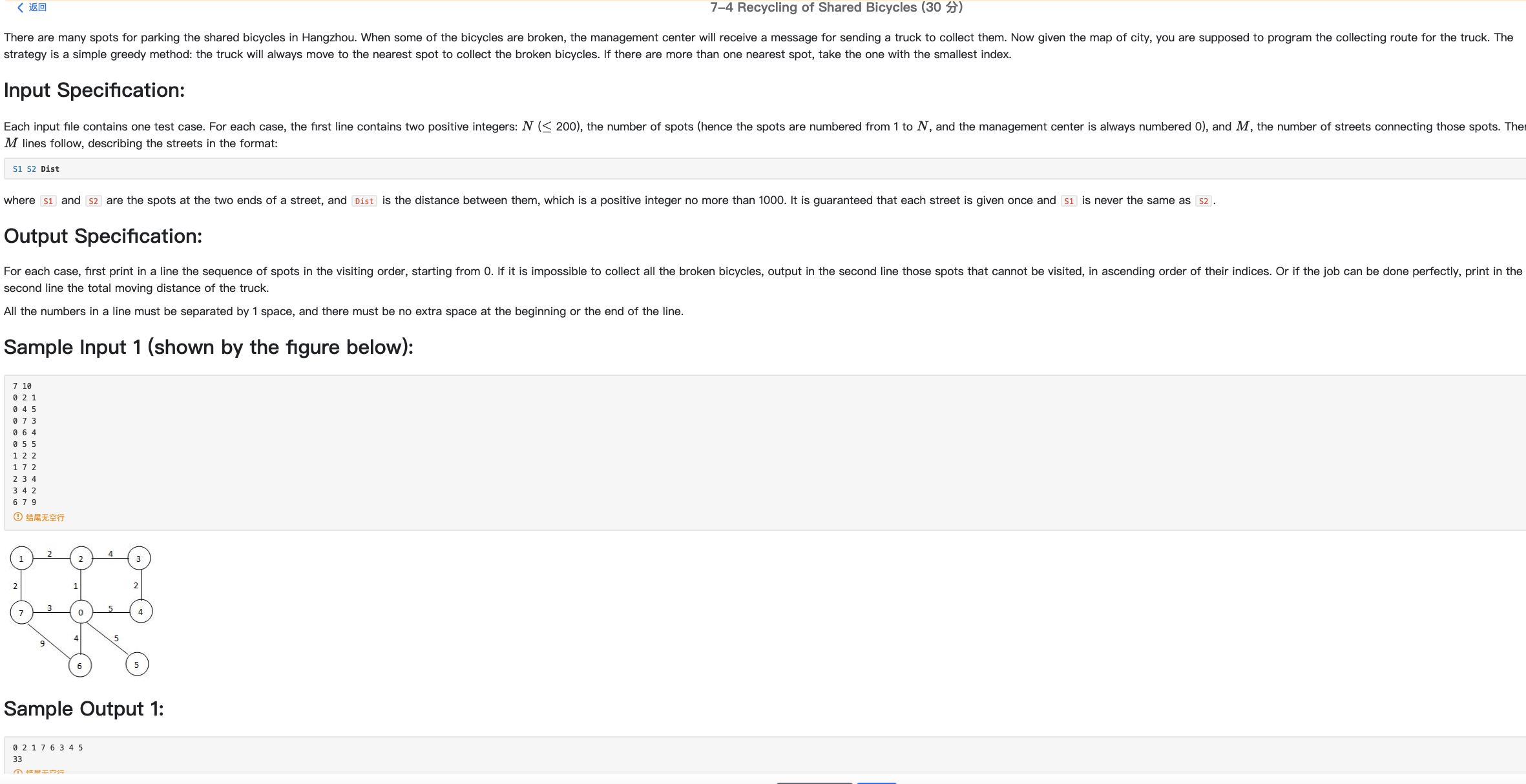
Investigate the typical examples of Floyd algorithm!
#include<bits/stdc++.h>
using namespace std;
const int INF = 1000000000;
const int MAXV = 205;
int d[MAXV][MAXV];
int n, m;
bool vis[MAXV] = {0};
int sum = 0;
void Floyd(){
for(int v=0; v<=n; v++){
for(int i=0; i<=n; i++){
for(int j=0; j<=n; j++){
if(d[i][v] + d[v][j] < d[i][j]){
d[i][j] = d[i][v] + d[v][j];
}
}
}
}
}
int main(){
int a, b, dis;
scanf("%d %d",&n,&m);
fill(d[0], d[0] + MAXV * MAXV, INF);
for(int i=0; i<n; i++) d[i][i] = 0;
for(int i=0; i<m; i++){
scanf("%d %d %d",&a,&b,&dis);
d[a][b] = d[b][a] = dis;
}
Floyd();
vector<int> path;
int begin = 0, next;
path.push_back(0);
vis[0] = 1;
while(1){
int MIN = INF;
for(int i=0; i<=n; i++){
if(!vis[i] && d[begin][i] < MIN){
MIN = d[begin][i];
next = i;
}
}
if(MIN == INF){
int flag = false;
printf("0");
for(int j=1; j<path.size(); j++) printf(" %d",path[j]);
printf("\n");
for(int j=0; j<=n; j++){
if(!vis[j]){
if(!flag){
flag = 1;
printf("%d",j);
}
else printf(" %d",j);
}
}
}
else{
path.push_back(next);
vis[next] = 1;
sum += d[begin][next];
begin = next;
if(path.size() == n+1){
printf("0");
for(int j=1; j<path.size(); j++){
printf(" %d",path[j]);
}
printf("\n%d",sum);
break;
}
}
}
}