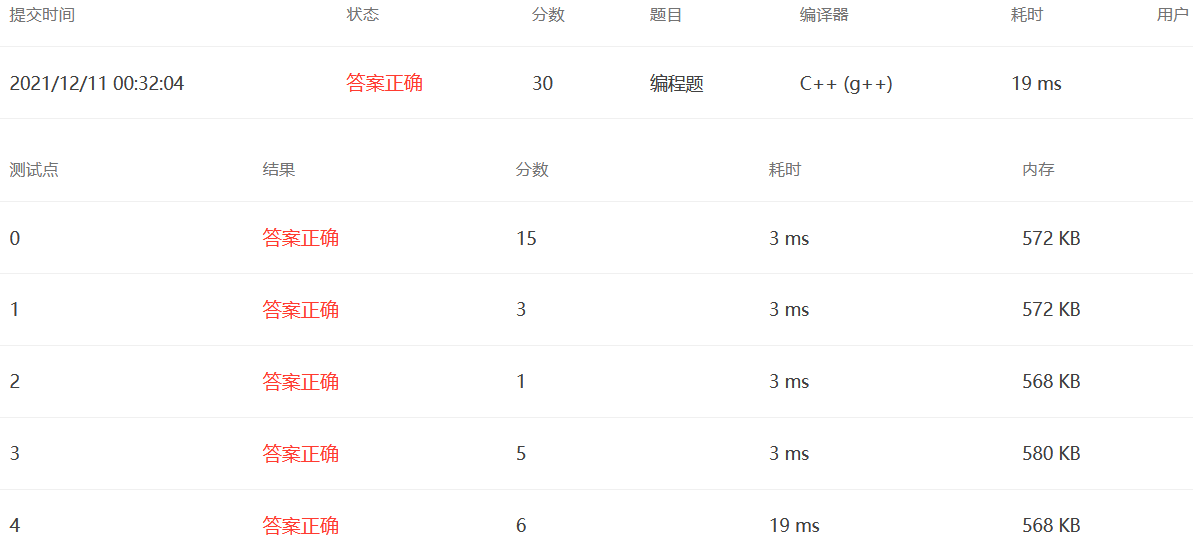
1. Arithmetic Progression of Primes (20 points)
In mathematics, an arithmetic progression (AP, equal difference column) is a sequence of numbers such that the difference between the consecutive terms is constant. In 2004, Terence Tao and Ben Green proved that for any positive n n n, there exists at least one arithmetic progression consists of n n n consecutive prime numbers. For example, { 7,37,67,97,127,157 } is one solution for n = 6 n=6 n=6. Now it is your job to find a maximum solution for a given n n n within a given range.
All the numbers in a line must be separated by a space, and there must be no extra space at the beginning or the end of the line.
Input Specification:
Each input file contains one test case, which gives two positive integers in a line: n ( ≤ 10 ) n\ (≤10) n (≤10), the number of consecutive prime terms in an arithmetic progression, and M A X P ( 2 ≤ M A X P < 1 0 5 ) MAXP\ (2≤MAXP<10^5) MAXP (2≤MAXP<105), the upper bound of the largest prime in the solution.
Output Specification:
For each test case, if there exists a solution, print in ascending order the prime numbers in a line. If the solution is not unique, output the one with the maximum common difference. If there is still a tie, print the one with the maximum first number. If there is no solution bounded by M A X P MAXP MAXP, output the largest prime in the given range instead.
Sample Input 1:
5 1000
Sample Output 1:
23 263 503 743 983
Sample Input 2:
10 200
Sample Output 2:
199
meaning of the title
For a given positive integer n n n, at a given upper limit M A X P MAXP Within MAXP, find one by n n Equal difference column of n prime numbers. If there is a solution, the column of prime numbers is output in ascending order. If the solution is not unique, then the output has the solution with the largest tolerance; If it is still not unique, the first largest solution of the output sequence is obtained. If M A X P MAXP If there is no solution in the MAXP range, the maximum prime number in the given range is output.
Solution Violence + Pruning
Theorems of Tao Zhexuan and Ben Green's Proof Green–Tao theorem . This question is very troublesome at first glance, and can be said to be the most difficult of the four questions to score, many of the code passed on the Internet also has problems. The potential pit is that the solution to understanding this problem is violence + pruning, and there is no other more effective way (?).
Therefore, we mark and collect all prime numbers within the data range before discussing them in categories as follows:
- When n = 1 n = 1 When n=1, the result is obviously M A X P MAXP The largest prime number in the MAXP range, consistent with insolubility.
- When n > 1 n > 1 When n>1, the outer loop iterates through all the collected prime numbers i n turn, taking the current prime number primes[i] as the first element of the sequence of equal difference of all prime numbers. The second loop starts with the known maximum equal difference curDiff and increments the curDiff continuously. Innermost loop validation, whether there is an equivariance starting with primes[i], curDiff, and length of n n n's sequence of equal difference of all prime numbers yields a more efficient solution when it exists - either with a larger first element or with a larger tolerance.
It's more complex, but with a little pruning, you can get through.
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
int n, maxp;
bitset<maxn> inp; // is not prime
vector<int> primes;
void getPrimes() {
inp[0] = inp[1] = 1;
for (int i = 2; i <= maxp; ++i) {
if (inp[i] == 0)
primes.push_back(i);
for (int j = i + i; j <= maxp; j += i)
inp[j] = 1;
}
}
int main() {
cin >> n >> maxp;
getPrimes(); // Find prime numbers in all ranges
if (n == 1) { // A two-point test point for a card when there is only one number in a number column
cout << primes.back();
return 0;
}
vector<int> tmp, ans;
int maxDiff = -1; // Traverse through each prime number in turn, starting with the prime number to find the tolerance that meets the criteria
for (int i = 0; i < primes.size(); ++i) {
int curDiff = (maxDiff == -1) ? 1 : maxDiff; // Prune
int x = primes[i];
while (true) {
if (x + (n - 1) * curDiff > maxp) break; // Prune
tmp.clear();
int k = x;
tmp.push_back(x);
for (int j = 1; j < n; ++j) {
k = k + curDiff;
if (inp[k] == 1) break;
tmp.push_back(k);
}
if (tmp.size() == n) {
ans = tmp;
maxDiff = curDiff;
}
++curDiff;
}
}
if(maxDiff == -1) {
printf("%d\n", primes.back());
return 0;
}
for (int i = 0; i < ans.size(); ++i) printf(" %d" + !i, ans[i]);
return 0;
}
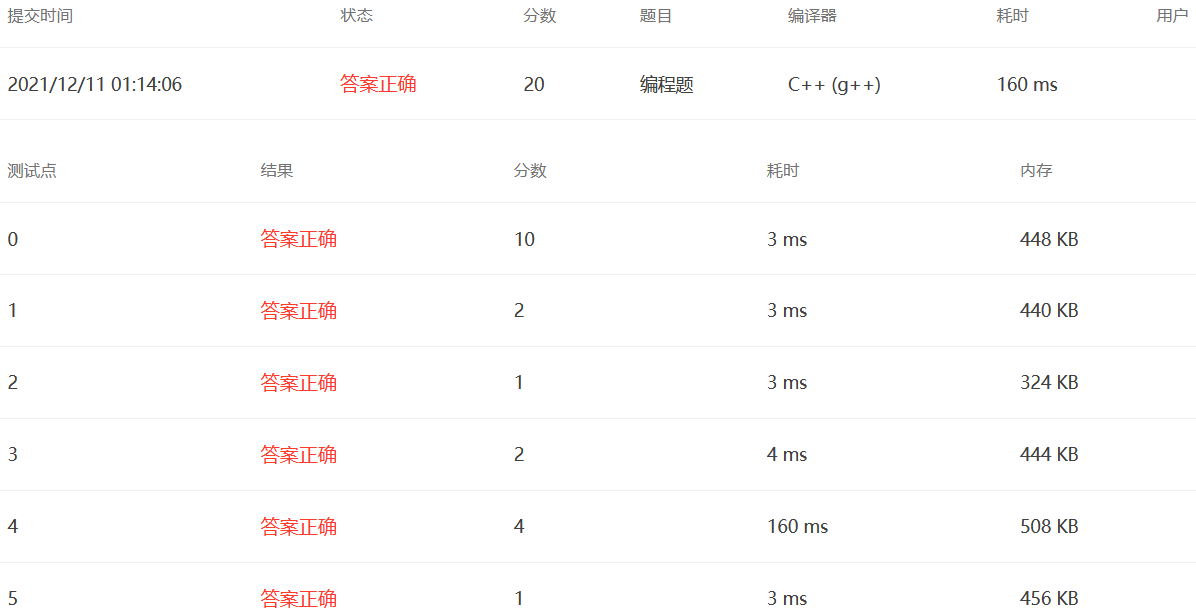
2. Lab Access Scheduling (25 points)
Nowadays, we have to keep a safe social distance to stop the spread of virus due to the COVID-19 outbreak. Consequently, the access to a national lab is highly restricted. Everyone has to submit a request for lab use in advance and is only allowed to enter after the request has been approved. Now given all the personal requests for the next day, you are supposed to make a feasible plan with the maximum possible number of requests approved. It is required that at most one person can stay in the lab at any particular time.
Input Specification:
Each input file contains one test case. Each case starts with a positive integer N N N ( ≤ 2 × 1 0 3 ) (≤2×10^3) (≤2×103), the number of lab access requests. Then N N N lines follow, each gives a request in the format:
hh:mm:ss hh:mm:ss
where hh:mm:ss represents the time point in a day by hour:minute:second, with the earliest time being 00:00:00 and the latest 23:59:59. For each request, the two time points are the requested entrance and exit time, respectively. It is guaranteed that the exit time is after the entrance time.
Note that all times will be within a single day. Times are recorded using a 24-hour clock.
Output Specification:
The output is supposed to give the total number of requests approved in your plan.
Sample Input:
7 18:00:01 23:07:01 04:09:59 11:30:08 11:35:50 13:00:00 23:45:00 23:55:50 13:00:00 17:11:22 06:30:50 11:42:01 17:30:00 23:50:00
Sample Output:
5
Hint:
All the requests can be approved except the last two.
meaning of the title
In order to prevent the spread of the epidemic, limited access to the laboratory is required. Everyone must submit an application for the use of the lab one day in advance and can enter the lab the next day only after the request has been approved. At most one person can be in the laboratory at a given point in time. Now with all the applications, it's your job to make a viable plan for the most people to use the lab.
A lab's request for use is a tuple of start and end times given in the form of 24 hours hh:mm:ss. All the time is in one day.
Solution Sorting+Interval Greed
This question is very simple, that is, interval greed has been done many times. Sort first so that the earliest requests end first; Set the known end time to curEnd and initialize to 0 0 0, and then iterate through the request array from scratch, adding one to the number of requests passed if the start time of the current request is greater than or equal to the known end time curEnd, updating that the known end time is the end time of the current request.
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e3 + 10;
int n, h1, m1, s1, h2, m2, s2;
struct node {
int bt, et; // begin time, end time;
} reqs[maxn];
int secs(int h, int m, int s) {
return h * 60 * 60 + m * 60 + s;
}
int main() {
cin >> n;
for (int i = 0; i < n; ++i) {
scanf("%d:%d:%d %d:%d:%d", &h1, &m1, &s1, &h2, &m2, &s2);
reqs[i].bt = secs(h1, m1, s1);
reqs[i].et = secs(h2, m2, s2);
}
sort(reqs, reqs + n, [&](const node &a, const node &b) {
return a.et != b.et ? a.et < b.et : a.bt < b.bt;
});
int cnt = 0, curEnd = 0;
for (int i = 0; i < n; ++i) {
if (reqs[i].bt >= curEnd) {
++cnt;
curEnd = reqs[i].et;
}
}
cout << cnt;
return 0;
}
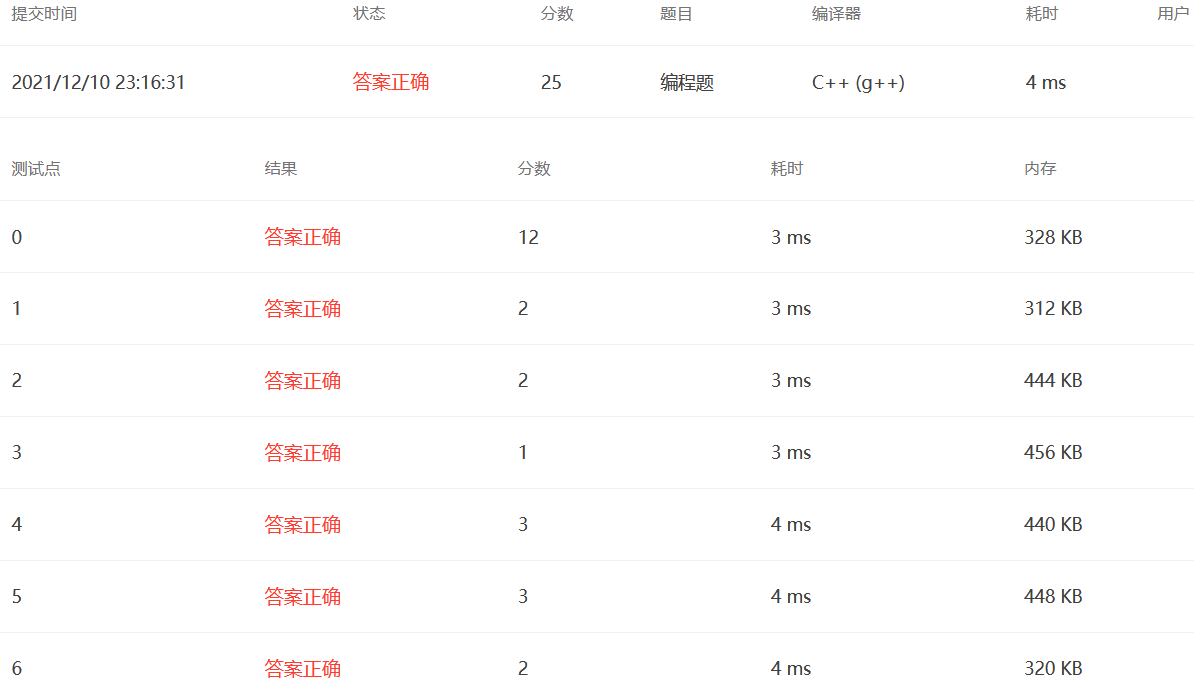
3. Structure of Max-Heap (25 points)
In computer science, a max-heap is a specialized tree-based data structure that satisfies the heap property: if P P P is a parent node of C C C, then the key (the value) of P P P is greater than or equal to the key of C C C. A common implementation of a heap is the binary heap, in which the tree is a complete binary tree.
Your job is to first insert a given sequence of integers into an initially empty max-heap, then to judge if a given description of the resulting heap structure is correct or not. There are 5 different kinds of description statements:
- x is the root
- x and y are siblings
- x is the parent of y
- x is the left child of y
- x is the right child of y
Input Specification:
Each input file contains one test case. For each case, the first line gives 2 positive integers: N N N ( ≤ 1 , 000 ) (≤1,000) (≤1,000), the number of keys to be inserted, and M M M ( ≤ 20 ) (≤20) (≤20), the number of statements to be judged. Then the next line contains N N N distinct integer keys in [ − 1 0 4 , 1 0 4 ] [−10^4,10^4] [−104,104] which are supposed to be inserted into an initially empty max-heap. Finally there are M M M lines of statements, each occupies a line.
Output Specification:
For each statement, print 1 if it is true, or 0 if not. All the answers must be print in one line, without any space.
Sample Input:
5 6 23 46 26 35 88 35 is the root 46 and 26 are siblings 88 is the parent of 46 35 is the left child of 26 35 is the right child of 46 -1 is the root
Sample Output:
011010
meaning of the title
The idea is simple, first insert a given sequence of integers into a maximum heap that is initially empty. For this existing maximum heap, a series of propositions are given - x is the root node, X and y are the brothers node, x is the father/left/right child node of y, and judge whether they are true or false.
Solution Build Heap+String Processing+Hash Table
The problem is not difficult, but rather cumbersome. Write a heap function first, since elements are unique, for subsequent processing to be efficient and simple, use a hash table to store the location of each element in the heap. Then, the input string is processed for different propositions, and the values of x and y are obtained. Then, the position of px, py in the heap is taken out from the hash table to determine if the proposition is satisfied, the output is 1, otherwise the output is 0.
#include <bits/stdc++.h>
#define father(i) ((i) / 2)
#define left(i) ((i) * 2)
#define right(i) (((i) * 2) + 1)
using namespace std;
const int maxn = 1010;
int n, m, val, x, y;
int h[maxn], len = 0;
unordered_map<int, int> rec;
string str;
void push(int v) {
h[++len] = v;
int cur = len;
for (int i = father(cur); i && h[i] < v; cur = i, i = father(cur))
h[cur] = h[i];
h[cur] = v;
}
vector<string> split(const string &s, char delim = ' ') { // Split string s into word sequences by spaces
if (s.empty()) return {};
size_t beginPos = s.find_first_not_of(delim, 0);
size_t endPos = s.find_first_of(delim, beginPos);
vector<string> ans;
while (beginPos != string::npos) {
ans.push_back(s.substr(beginPos, endPos - beginPos));
beginPos = s.find_first_not_of(delim, endPos);
endPos = s.find_first_of(delim, beginPos);
}
return ans;
}
int main() {
cin >> n >> m;
for (int i = 0; i < n; ++i) {
cin >> val;
push(val);
}
for (int i = 1; i <= n; ++i) rec[h[i]] = i;
while (m--) {
cin >> x;
int px = rec[x];
getline(cin, str);
if (!px) {
printf("0");
continue;
}
vector<string> &&tokens = split(str);
bool flag = false;
if (str.back() == 't') { // Is Root Node
if (h[1] == x) flag = true;
}
else if (str.back() == 's') { // Brother Node
int y = stoi(tokens[1]), py = rec[y];
if (py && px != py && father(px) == father(py)) flag = true;
}
else if (tokens[2] == "parent") { // Parent Node
int y = stoi(tokens.back()), py = rec[y];
int fa = father(py);
if (py && fa > 0 && fa <= n && fa == px) flag = true;
}
else if (tokens[2] == "left") { // Left Node
int y = stoi(tokens.back()), py = rec[y];
int l = left(py);
if (py && l <= n && l == px) flag = true;
}
else if (tokens[2] == "right") { // Right Node
int y = stoi(tokens.back()), py = rec[y];
int r = right(py);
if (py && r <= n && r == px) flag = true;
}
printf(flag ? "1" : "0");
}
return 0;
}

4. Recycling of Shared Bicycles (30)
There are many spots for parking the shared bicycles in Hangzhou. When some of the bicycles are broken, the management center will receive a message for sending a truck to collect them. Now given the map of city, you are supposed to program the collecting route for the truck. The strategy is a simple greedy method: the truck will always move to the nearest spot to collect the broken bicycles. If there are more than one nearest spot, take the one with the smallest index.
Input Specification:
Each input file contains one test case. For each case, the first line contains two positive integers: N N N ( ≤ 200 ) (≤ 200) (≤200), the number of spots (hence the spots are numbered from 1 1 1 to N N N, and the management center is always numbered 0 0 0), and M M M, the number of streets connecting those spots. Then M M M lines follow, describing the streets in the format:
S1 S2 Dist
where S1 and S2 are the spots at the two ends of a street, and Dist is the distance between them, which is a positive integer no more than 1000. It is guaranteed that each street is given once and S1 is never the same as S2.
Output Specification:
For each case, first print in a line the sequence of spots in the visiting order, starting from 0. If it is impossible to collect all the broken bicycles, output in the second line those spots that cannot be visited, in ascending order of their indices. Or if the job can be done perfectly, print in the second line the total moving distance of the truck.
All the numbers in a line must be separated by 1 space, and there must be no extra space at the beginning or the end of the line.
Sample Input 1 (shown by the figure below):
7 10 0 2 1 0 4 5 0 7 3 0 6 4 0 5 5 1 2 2 1 7 2 2 3 4 3 4 2 6 7 9

Sample Output 1:
0 2 1 7 6 3 4 5 33
Sample Input 2:
7 8 0 2 1 0 4 5 0 7 3 1 2 2 1 7 2 2 3 4 3 4 2 6 5 1
Sample Output 2:
0 2 1 7 3 4 5 6
meaning of the title
There are many places in Hangzhou to park shared bicycles. When some bicycles are damaged, the management center will receive a message and collect them with a truck. Now, given a map of the city, you need to program and calculate the routes that trucks collect these bicycles. The strategy is simple greed: trucks always move to the nearest location to collect the broken bicycles; If there is more than one nearest location, select the one with the smallest number.
First, print a sequence of places in the order in which they are visited. If the truck can collect all the broken bicycles in all locations, it outputs the total distance the truck moves, otherwise it outputs those locations that are not accessible.
Solution Shortest Route+DFS
The problem is really simple. The pit is to correctly understand the greedy strategy of truck movement - Trucks always move to the next place nearest to their current location, possibly going through other visited places halfway, but not outputting those already visited places. It's impossible to go through places you haven't visited halfway, because the next destination won't be the nearest. Therefore, we use the full-source shortest-path algorithm Floyd-Warshall to calculate the shortest distance from all locations to all other locations.
Then from the location of the management center (vertex 0), run the greed policy recursively and move to the next nearest location until all locations have been visited or cannot access other locations, calculating the total distance moved.
#include <bits/stdc++.h>
using namespace std;
const int maxn = 210;
const int inf = 0x3f3f3f3f;
int n, m, s1, s2, d;
int g[maxn][maxn];
bool vis[maxn];
void floyd() {
for (int k = 0; k <= n; ++k) {
for (int i = 0; i <= n; ++i) {
if (g[i][k] != inf) {
for (int j = 0; j <= n; ++j) {
if (g[k][j] != inf)
g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
}
}
}
}
}
int pathDist = 0;
vector<int> path;
void dfs(int u) {
vis[u] = true;
path.push_back(u);
int v = -1, minDist = inf;
for (int i = 0; i <= n; ++i) {
if (!vis[i] && g[u][i] < minDist) {
v = i;
minDist = g[u][i];
}
}
if (v == -1 || minDist == inf) return;
pathDist += minDist;
dfs(v);
}
int main() {
cin >> n >> m;
memset(g, 0x3f, sizeof(g));
// for (int i = 0; i <= n; ++i) for (int j = 0; j <= n; ++j) if (i == j) g[i][j] = 0;
for (int i = 0; i < m; ++i) {
cin >> s1 >> s2 >> d;
g[s1][s2] = g[s2][s1] = d;
}
floyd();
dfs(0);
for (int i = 0; i < path.size(); ++i) printf(" %d" + !i, path[i]);
cout << endl;
if (path.size() == n + 1) { // Collect all broken bikes
cout << pathDist;
} else {
vector<int> ans;
for (int i = 0; i <= n; ++i)
if (!vis[i]) ans.push_back(i);
for (int i = 0; i < ans.size(); ++i) printf(" %d" + !i, ans[i]);
}
return 0;
}