Two points search

Binary Search, also known as Binary Search, is an efficient search method. However, half search requires that the linear table must adopt the sequential storage structure, and the elements in the table are ordered by keywords.

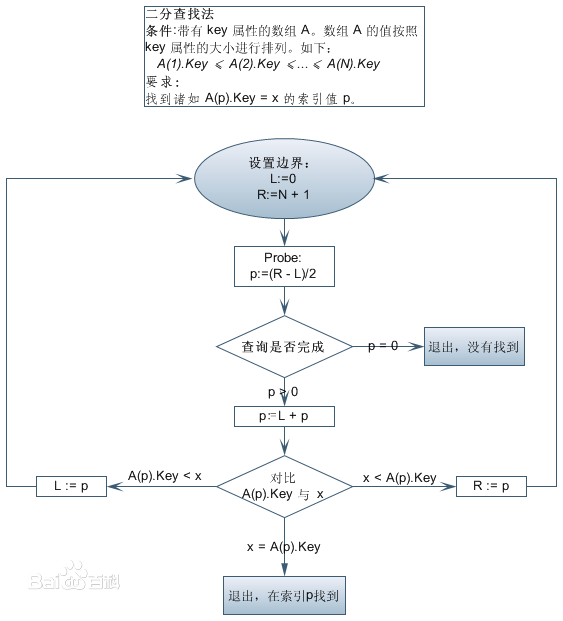
Algorithm requirements

1. Sequential storage structure must be adopted.
2. The keywords must be arranged in order.

Algorithm steps

In fact, binary search is also relatively easy to understand. It may be divided into two parts. Then, compare the two sides, keep the effective interval, and continue searching in two parts until it is found or beyond the interval. Therefore, the basic steps of binary search are:

1. Determine the interval to be searched
2. Determine the reference point for dichotomy
3. Select the bisection point in the interval
4. According to the value of the bisection point, synthesize the left and right interval conditions and the purpose of the solution, and cut off half of the useless intervals.
5. Continue to repeat the above steps in the effective range

Code example

Here, we mainly use non recursion and recursion to search. The code is as follows:

1. Non recursive search

/*
    * Binary search (also called half search) - non recursive
    * array $arr Interval to be found
    * int $number Lookup number
    * int Return found key 
    */
    public function binarySearch($arr,$number){
         
        //If the interval to be searched is not an array or empty, return - 1
        if(!is_array($arr) || empty($arr)){
            return -1;
        }
        sort($arr); //Binary search key
        $len=count($arr);
        $lower=0;
        $high=$len-1;

        //If the low point is less than the high point, exit
        while($lower<=$high){
            //Comparison with middle point as reference point
            $middle=intval(($lower+$high)/2);
            if($arr[$middle]>$number){
                //The number of lookups is smaller than the reference value, and the right side is rounded off.
                $high=$middle-1;
            }else if($arr[$middle]<$number){
                //The number of lookups is larger than the reference value, and the left side is removed.
                $lower=$middle+1;
            }else{
                //If the number of lookups is equal to the reference point, return
                return $middle;
            }
        }
        return -1;
    }

2. Recursive search

/*
    * Binary search (also called half search) - recursion
    * array $arr Interval to be found
    * int $number Lookup number
    * int $lower  Low point
    * int $high   High point
    */

    public function binarySearchRecursion($arr,$number,$lower,$high)
    {    
        //If the interval to be searched is not an array or empty, return - 1
        if(!is_array($arr) || empty($arr)){
            return -1;
        }
        sort($arr);
        $len=count($arr);
        $middle=intval(($lower+$high)/2);
        if($arr[$middle]>$number){
            //The number of lookups is smaller than the reference value, and the right side is rounded off.
            return $this->binarySearchRecursion($arr,$number,0,$middle-1);
        }elseif($arr[$middle]<$number){
            //The number of lookups is larger than the reference value, and the left side is removed.
            return $this->binarySearchRecursion($arr,$number,$middle+1,$high);
        }else{
            //If the number of lookups is equal to the reference value, return
            return $middle;
        }
        //- 1 if not found
        return -1;
    }

Algorithm usage

The requirement is to find the location of $number in the interval $arr to be searched. The call algorithm is as follows:

//Array of interval to be searched
$arr=array(1,2,3,4,5,6,7,10,12,14,18,16,20);
//Non recursive find 25 in $arr
$binaryKey=$this->binarySearch($arr,25);
//Recursively find 12 locations in $arr
$binarySearchRecursionKey=$this->binarySearchRecursion($arr,1,12,count($arr)-1);
 //Printout
 print_r($binaryKey);
 echo '//';
 print_r($binarySearchRecursionKey);

Output result
-1//8

Time complexity analysis

In an ordered array, if a violent algorithm is used to search, that is, to traverse and compare one by one, the time complexity is O(n); however, after binary search, because half of the search interval can be lost each time, the time complexity will be reduced to O(logn), and the algorithm is better. ( A detailed explanation of the time and space complexity of the algorithm)

Related information

Two part search of PHP algorithm