Pilot pairing scheme problem

Title Description

Core ideas

Find the maximum matching of bipartite graph and output any matching scheme

This problem can be solved directly by Hungarian algorithm, and the time complexity is O ( n m ) O(nm) O(nm). However, it can also be solved by network flow, and the time complexity is O ( m n ) O(m\sqrt n) O(mn ) it can be seen that the efficiency is greatly increased after using the network flow algorithm.

Conclusion:

• A feasible flow in the network flow corresponds to a set of matches in the bipartite graph
• The maximum flow in the network flow corresponds to the maximum matching of the bipartite graph

Therefore, we want to find the maximum matching of bipartite graph, so we can use Dinic algorithm to find the maximum flow of this network.

So, let's think about how to build this network diagram?

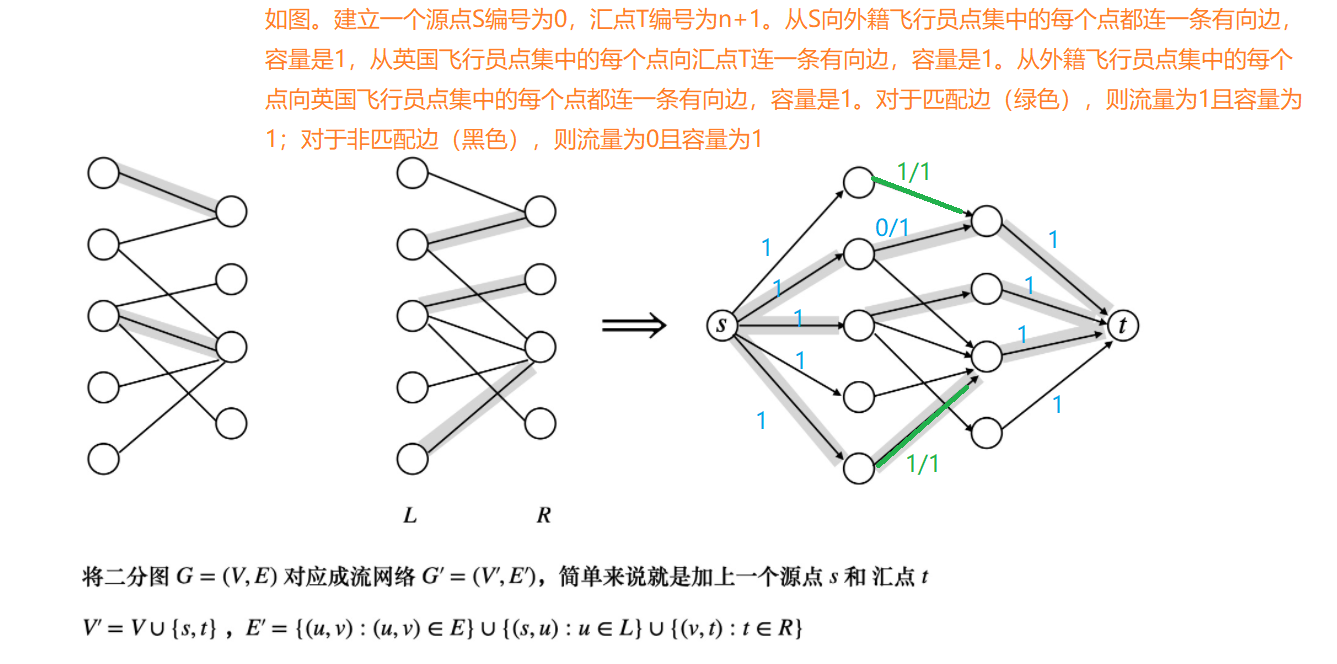
So how do we output the matching scheme?

We can traverse all positive edges if we find that the capacity of the edge is 0 0 0, then this side is used to form a group of schemes. Specifically, enumerate the positive edges. If the end number of this positive edge is [m+1,n], it means that this positive edge is an edge between the foreign pilot point set and the British pilot point set, and then we judge the capacity of this edge f [ i ] f[i] Whether f[i] is 0. If it is 0, it means it is a matching edge. Then we can output the starting point e[i^1] of the matching edge and the ending point e[i] of the matching edge.

Note: for the calculation of the number of edges, the worst case is that the left point set is 50 50 50, the point set on the right is 50 50 50, then there will be 50 × 50 = 2500 50\times 50=2500 fifty × 50 = 2500 edges. Since the network diagram needs to establish reverse edges, it needs to be opened twice, i.e 2500 × 2 = 5000 2500\times2=5000 two thousand and five hundred × 2 = 5000, and then from the source point S S S to the left 50 50 50 points need to be connected 50 50 50, similarly, from the right side 50 50 50 point-to-point meeting points T T T needs to be connected 50 50 50, because the reverse edge needs to be established, it is ( 50 + 50 ) × 2 = 200 (50+50)\times2=200 (50+50) × 2 = 200, so the total number of sides required is 5000 + 200 = 5200 5000+200=5200 5000+200=5200.

code

The network flow Dinic algorithm solves the maximum matching of bipartite graph:

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=110,M=5210,INF=1e8;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];
int n,m,S,T;

void add(int a,int b,int c)
{
    e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++;
    e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++;
}

bool bfs()
{
    int hh=0,tt=0;
    memset(d,-1,sizeof d);
    q[0]=S,d[S]=0,cur[S]=h[S];
    while(hh<=tt)
    {
        int t=q[hh++];
        for(int i=h[t];~i;i=ne[i])
        {
            int ver=e[i];
            if(d[ver]==-1&&f[i])
            {
                d[ver]=d[t]+1;
                cur[ver]=h[ver];
                if(ver==T)
                    return true;
                q[++tt]=ver;
            }
        }
    }
    return false;
}

int find(int u,int limit)
{
    if(u==T)
        return limit;
    int flow=0;
    for(int i=cur[u];~i&&flow<limit;i=ne[i])
    {
        cur[u]=i;
        int ver=e[i];
        if(d[ver]==d[u]+1&&f[i])
        {
            int t=find(ver,min(f[i],limit-flow));
            if(!t)
                d[ver]=-1;
            f[i]-=t;
            f[i^1]+=t;
            flow+=t;
        }
    }
    return flow;
}

int dinic()
{
    int maxflow=0;
    int flow;
    while(bfs())
    {
        while(flow=find(S,INF))
            maxflow+=flow;
    }
    return maxflow;
}

int main()
{
    memset(h,-1,sizeof h);
    scanf("%d%d",&m,&n);
    //Since the point set number on the left is [1,m], the point set number on the right is [m+1,n]
    //Therefore, the numbers given to the source point and sink point cannot exist in the left point set and the right point set
    S=0,T=n+1;
    //Connect a directed edge with capacity of 1 from the source point S to the left point set
    for(int i=1;i<=m;i++)
        add(S,i,1);
    //Connect a directed edge with capacity of 1 from the right point set to the sink point T    
    for(int i=m+1;i<=n;i++)
        add(i,T,1);
    int a,b;
    //Connect a directed edge with capacity of 1 from the left point set to the right point set 
    while(scanf("%d%d",&a,&b),a!=-1&&b!=-1)
        add(a,b,1);
    printf("%d\n",dinic());
    //Traverse all the positive edges to find the matching edges between the left point set and the right point set
    for(int i=0;i<idx;i+=2)
    {
        if(e[i]>m&&e[i]<=n&&!f[i])
            printf("%d %d\n",e[i^1],e[i]);
    }
    return 0;
}

Hungarian algorithm to solve the maximum matching of bipartite graph:

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=110,M=5210;
int h[N],e[M],ne[M],idx;
int match[N];
bool st[N];
int n,m,S,T;

void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

bool find(int u)
{
    for(int i=h[u];~i;i=ne[i])
    {
        int v=e[i];
        if(!st[v])
        {
            st[v]=true;
            if(!match[v]||find(match[v]))
            {
                match[v]=u;
                return true;
            }
        }
    }
    return false;
}

int main()
{
    memset(h,-1,sizeof h);
    scanf("%d%d",&m,&n);
    int a,b;
    while(scanf("%d%d",&a,&b),a!=-1&&b!=-1)
        add(a,b);
    int res=0;
    for(int i=1;i<=n;i++)
    {
        memset(st,0,sizeof st);
        if(find(i))
            res++;
    }
    printf("%d\n",res);
    for(int i=m+1;i<=n;i++)
    {
        if(match[i])
            printf("%d %d\n",match[i],i);
    }
    return 0;
}