Central town problem

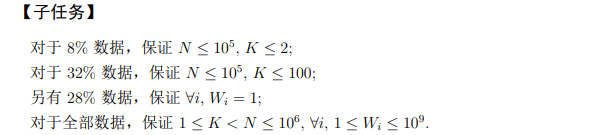
Problem solution

In essence, it is a very classic long chain dissection dp problem.

We can remember d p u , i dp_{u,i} dpu,i indicates at a point u u u is in the subtree of the root node, and the depth of the deepest special point is i i i is the maximum value of the total weight.
Our transfer is mainly divided into two parts: merging two subtrees and assigning the root node of the current subtree as a special point.

For the first transfer, we need to ensure that the distance between the shallowest special points of the merged two subtrees is not less than K K K, the transfer formula is
d p u , i = min ⁡ min ⁡ ( j , k ) = i ∧ j + k − 2 d e p u ⩾ K d p u , j + d p v , k dp_{u,i}=\min_{\min(j,k)=i\wedge j+k-2dep_u\geqslant K}dp_{u,j}+dp_{v,k} dpu,i = min(j,k)=i Λ j+k − 2depu ⩾ Kmin dpu,j + dpv,k ⩾ but enumeration is required j , k j,k j. K two, obviously T T T flies, but we observe that the above state can be optimized by the maximum suffix. We will d p u , i dp_{u,i} Change the definition of dpu,i ， to point u u In the subtree with u as the root, the depth of the deepest special point shall not be less than i i i is the maximum value of the total weight.
d p u , i = min ⁡ ( d p u , i + d p v , d e p u + K − i , d p v , i + d p u , d e p u + K − i ) dp_{u,i}=\min(dp_{u,i}+dp_{v,dep_u+K-i},dp_{v,i}+dp_{u,dep_u+K-i}) dpu,i = min(dpu,i + dpv,depu + K − i, dpv,i + dpu,depu + K − i), but in fact, after transfer, it does not really make the d p u , i dp_{u,i} dpu,i ， indicates the previous definition d p u , i dp_{u,i} The maximum suffix of dpu,i ， because it limits j j j is accumulated to i i i is bound to make the j j The transfer range of j is reduced, that is to say, it exists j + k ⩾ K + 2 d e p u > i + K j+k\geqslant K+2dep_u>i+K j+k ⩾ K+2depu > I + K.
In this case, we might as well do the suffix minimum again after the transfer. Obviously, after merging the two subtrees, if v v There is a special point in v, that is, if there is a contribution, we will affect it d p u , i dp_{u,i} dpu,i + i i i must not exceed v v The depth of the deepest node in the v subtree. Therefore, the time complexity of the maximum suffix we made is the same as that of the previous transfer O ( max ⁡ v ′ ∈ T v d e p v ) O\left(\max_{v'\in T_v}dep_v\right) O(maxv ′∈ Tv depv), i.e. the longest chain length.
In this case, we can think of optimizing our design by long-chain subdivision d p dp dp transfer, merging short chains into long chains at a time.

The second part is to transfer our current u u u is assigned as a special point. Obviously, in this case, it is necessary to ensure that the existing special points are consistent with u u u distance not less than K K K. That is, the depth is not less than d e p u + K dep_u+K depu + K, our d p dp dp is the maximum value of the maintained suffix, with transfer type,
d p u , d e p u = v a l u + d p u , d e p u + K dp_{u,dep_u}=val_u+dp_{u,dep_u+K} dpu,depu = valu + dpu,depu + K O ( 1 ) O\left(1\right) O(1), which is now at the top, does not affect other suffixes.

The whole is a long chain subdivision optimization d p dp In the process of dp, each chain will only make a contribution once, and then it will be merged into the long chain. In the future, the long chain will make a contribution, right O ( n ) O\left(n\right) O(n). However, heavy chain subdivision can also be too, and the time complexity may not be the same as the space complexity.

Time complexity O ( n ) O\left(n\right) O (n) (long chain) or O ( n log ⁡   n ) O\left(n\log\,n\right) O (nlogn) (heavy chain).

Source code

#include<bits/stdc++.h>
using namespace std;
#define MAXN 1000005
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
#define lson (rt<<1)
#define rson (rt<<1|1)
typedef long long LL;
typedef unsigned long long uLL; 
typedef long double ld;
typedef pair<int,int> pii;
const int INF=0x3f3f3f3f;
const int mo=1e9+7;
const int mod=1e5+3;
const int inv2=5e8+4;
const int jzm=2333;
const int zero=2000;
const int n1=1000;
const int M=100000;
const int orG=3,ivG=332748118;
const long double Pi=acos(-1.0);
const double eps=1e-12;
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){
	_T f=1;x=0;char s=getchar();
	while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}
	while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
	x*=f;
}
template<typename _T>
void print(_T x){if(x<0){x=(~x)+1;putchar('-');}if(x>9)print(x/10);putchar(x%10+'0');}
int gcd(int a,int b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1)t=1ll*t*a%p;a=1ll*a*a%p;s>>=1;}return t;}
int n,K,val[MAXN],dep[MAXN],head[MAXN],tot;
int siz[MAXN],wson[MAXN],id[MAXN],mxd[MAXN],stak;
LL f[22][MAXN],g[MAXN],ans;
struct edge{int to,nxt;}e[MAXN<<1];
void addEdge(int u,int v){e[++tot]=(edge){v,head[u]};head[u]=tot;}
void dosaka1(int u,int fa){
	siz[u]=1;dep[u]=dep[fa]+1;
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;if(v==fa)continue;
		dosaka1(v,u);siz[u]+=siz[v];mxd[u]=max(mxd[u],mxd[v]);
		if(siz[v]>siz[wson[u]])wson[u]=v;
	}
}
void dosaka2(int u,int fa){
	mxd[u]=dep[u];if(wson[u])id[wson[u]]=id[u],dosaka2(wson[u],u),mxd[u]=mxd[wson[u]];
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;if(v==fa||v==wson[u])continue;
		id[v]=++stak;dosaka2(v,u);
		for(int j=dep[u]+1;j<=min(dep[u]+K,mxd[v]);j++){
			int k=max(j,dep[u]+dep[u]+K-j);
			if(k<=mxd[v])g[j]=max(f[id[u]][j]+f[id[v]][k],g[j]);else g[j]=max(f[id[u]][j],g[j]);
			if(k<=mxd[u])g[j]=max(f[id[v]][j]+f[id[u]][k],g[j]);else g[j]=max(f[id[v]][j],g[j]);
		}
		for(int j=min(mxd[v],dep[u]+K);j>dep[u];j--)
			f[id[u]][j]=max(f[id[u]][j+1],g[j]),g[j]=f[id[v]][j]=0;
		mxd[u]=max(mxd[v],mxd[u]);stak--;
	}
	f[id[u]][dep[u]]=(LL)val[u];
	if(mxd[u]>=dep[u]+K)f[id[u]][dep[u]]+=f[id[u]][dep[u]+K],f[id[u]][dep[u]+K]=0;
	f[id[u]][dep[u]]=max(f[id[u]][dep[u]],f[id[u]][dep[u]+1]);
}
signed main(){
	//freopen("central.in","r",stdin);
	//freopen("central.out","w",stdout);
	read(n);read(K);for(int i=1;i<=n;i++)read(val[i]);K++;
	for(int i=1;i<n;i++){
		int u,v;read(u);read(v);
		addEdge(u,v);addEdge(v,u);
	}
	dosaka1(1,0);id[1]=++stak;dosaka2(1,0);
	for(int i=1;i<=min(mxd[1],K);i++)ans=max(ans,f[id[1]][i]);
	printf("%lld\n",ans);
	return 0;
}