Title Link: poj 2286 The Rotation Game
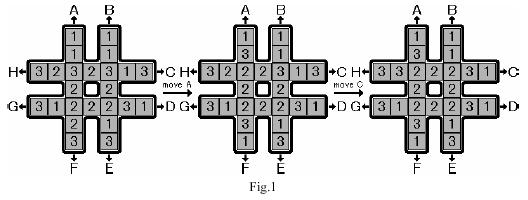
Title Purpose: make the values of the middle 8 elements the same by rotating in 8 directions. Examples are as follows:
I. problem solving instructions
#1 note: during Rotation, the matrix data needs to be re assigned, otherwise it will change together.
#2. Note: the operation procedure is stored in a queue. When assigning a queue to a new queue, you need to pay special attention to the order of elements in the queue, because it corresponds to the operation order.
new_step = []
new_step.append(dir_i)
for step_i in step:
new_step.append(step_i)
# Ensure that the order cannot be changed, otherwise the order will be wrong when the final output is made
new_step.append(dir_i) # Add at tail
# And remove the data of the head
new_step.pop(0)
# Set the number corresponding to each operation in advance:
# Set operation flag
action = {0:['A'],1:['B'],2:['C'],3:['D'],4:['E'],5:['F'],6:['G'],7:['H']}
#3. Determination of target elements: count the number of 1 / 2 / 3 three elements in the target area, and take the element corresponding to the largest number as the target element. See findTarget function
#4 some rules:
#4.1 if the target element changes after one rotation, return
#4.2 after one rotation, if the target element does not change but the number decreases, return
#4.3 after one rotation, if the target elements do not change and the number does not decrease, enter the next dfs search;
#5 termination conditions
#5.1 the number of target elements in the target area is 8. return successfully!
#5.1. 1. Save the current scheme
#5.1. 2 store the current target element
#5.2 if the DFS search depth is greater than the set value, an error return s.
#5.3 assuming that the current target element can find a feasible scheme, other target elements will not be searched.
#5.4 analyze all schemes of the current target element and select the scheme with the shortest length and sorted alphabetically.
#5.4. 1. Each operation is represented in Arabic numerals, the feasible scheme is spliced into a string, and the scheme with the smallest alphabetical order is determined according to the number size corresponding to the string.
II. Code implementation:
# http://www.mianshigee.com/question/16649hrq
import collections
import math
#1 note: during Rotation, the matrix data needs to be re assigned, otherwise it will change together.
#2. Precautions: use the queue to store the operation process. When assigning a queue to a new queue, you need to pay special attention to the order of elements in the queue, because it corresponds to the operation order.
# new_step = []
# new_step.append(dir_i)
# for step_i in step:
# new_step.append(step_i)
# # Ensure that the order cannot be changed, otherwise the order will be wrong when the final output is made
# new_step.append(dir_i) # Add at tail
# # And remove the data of the head
# new_step.pop(0)
#3. Determination of target elements: count the number of 1 / 2 / 3 three elements in the target area, and take the element corresponding to the largest number as the target element. See findTarget function
#4 some rules:
#4.1 if the target element changes after one rotation, return
#4.2 after one rotation, if the target element does not change but the number decreases, return
#4.3 after one rotation, if the target elements do not change and the number does not decrease, enter the next dfs search;
#5 termination conditions
#5.1 the number of target elements in the target area is 8. return successfully!
#5.1. 1. Save the current scheme
#5.1. 2 store the current target element
#5.2 If DFS If the search depth is greater than the set value, an error occurs return. // self.MaxDeep = 4 # this data is particularly effective and helps to improve the execution speed of the algorithm.
#5.3 assuming that the current target element can find a feasible scheme, other target elements will not be searched.
#5.4 analyze all schemes of the current target element and select the scheme with the shortest length and sorted alphabetically.
#5.4. 1. Each operation is represented in Arabic numerals, the feasible scheme is spliced into a string, and the scheme with the smallest alphabetical order is determined according to the number size corresponding to the string.
# Convert data to matrix
def data2Matrix(subData):
newData = [[0]*7 for i in range(7)]
# Fill the data of subData into
for i in range(24):
if i == 0:
newData[0][2] = subData[i]
elif i == 1:
newData[0][4] = subData[i]
elif i == 2:
newData[1][2] = subData[i]
elif i == 3:
newData[1][4] = subData[i]
elif 4<=i<=10:
newData[2][i-4] = subData[i]
elif i ==11:
newData[3][2] = subData[i]
elif i == 12:
newData[3][4] = subData[i]
elif 13<=i<=19:
newData[4][i-13] = subData[i]
elif i == 20:
newData[5][2] = subData[i]
elif i == 21:
newData[5][4] = subData[i]
elif i == 22:
newData[6][2] = subData[i]
elif i == 23:
newData[6][4] = subData[i]
return newData
# Find the elements of the target area and sort them
def findTarget(subData):
# Count the number of each element
num1 = 0
num2 = 0
num3 = 0
# List of coordinates for a given target area
Target_areas = [[2,2],[2,3],[2,4],[3,2],[3,4],[4,2],[4,3],[4,4]]
# res = ''#Store data
for i in range(8):
rr,cc = Target_areas[i][0],Target_areas[i][1]
# res = res + str(newData[rr][cc])
if subData[rr][cc] == 1:
num1 = num1 + 1
elif subData[rr][cc] == 2:
num2 = num2 + 1
elif subData[rr][cc] == 3:
num3 = num3 + 1
ans = [num1,num2,num3]
min_ans = min(ans)
max_ans = max(ans)
targetdict = {}
for i in range(1,4,1):
if ans[i-1] == max_ans and 'max' not in targetdict.keys():
targetdict['max'] = [i,max_ans] # Description of archived data [element value, element quantity]
elif ans[i-1] == min_ans and 'min' not in targetdict.keys():
targetdict['min'] = [i, min_ans]
else:
targetdict['mid'] = [i, ans[i-1]]
return targetdict
# Set the rotation and return the rotated matrix and the dictionary of the target area
def Rotation(Data,dir):
# Data needs to be transferred
subData = []
for i in range(len(Data)):
temp = []
for j in range(len(Data[0])):
temp.append(Data[i][j])
subData.append(temp)
if dir == 0: #Rotate 1 time in 0 direction
temp = subData[0][2]
for i in range(7):
if i == 6:
subData[i][2] = temp
else:
subData[i][2] = subData[i+1][2]
elif dir == 1: #Rotate once in direction 1
temp = subData[0][4]
for i in range(7):
if i == 6:
subData[i][4] = temp
else:
subData[i][4] = subData[i+1][4]
elif dir == 2:
temp = subData[2][6]
for i in range(6,-1,-1):
if i == 0:
subData[2][0] = temp
else:
subData[2][i] = subData[2][i-1]
elif dir == 3:
temp = subData[4][6]
for i in range(6,-1,-1):
if i == 0:
subData[4][0] = temp
else:
subData[4][i] = subData[4][i-1]
elif dir == 4:
temp = subData[6][4]
for i in range(6,-1,-1):
if i == 0:
subData[0][4] = temp
else:
subData[i][4] = subData[i - 1][4]
elif dir == 5:
temp = subData[6][2]
for i in range(6,-1,-1):
if i == 0:
subData[0][2] = temp
else:
subData[i][2] = subData[i - 1][2]
elif dir == 6:
temp = subData[4][0]
for i in range(7):
if i == 6:
subData[4][6] = temp
else:
subData[4][i] = subData[4][i+1]
elif dir == 7:
temp = subData[2][0]
for i in range(7):
if i == 6:
subData[2][6] = temp
else:
subData[2][i] = subData[2][i+1]
## Get the rotated data and the 8 target elements in the middle
targetdict = findTarget(subData)
return subData,targetdict
# Find the scheme with the smallest length and save it
def findWays(ways):
LEN = len(ways)
if LEN == 1:
return ways[0]
else:
Init_len = math.inf
FianlWays = []
for i in range(LEN):
temp = ways[i][0]
if len(temp) < Init_len: # Determine the minimum length of the scheme
Init_len = len(temp)
for i in range(LEN):# Find the scheme with the smallest length
temp = ways[i][0]
if len(temp) == Init_len:
FianlWays.append(ways[i])
## Look for the scheme with the same length but the smallest alphabetical order
LEN = len(FianlWays)
if LEN==1:
return FianlWays[0]
else:
len2 = len(FianlWays[0][0])
Init_int = math.inf
for i in range(LEN):
temp = FianlWays[i][0]
res = ''
for j in range(len2):
res = res + str(temp[j])
if int(res) < Init_int: # Find alphabetic minimum
Init_int = int(res)
## Determine the scheme corresponding to the minimum value of alphabetic sorting
for i in range(LEN):
temp = FianlWays[i][0]
res = ''
for j in range(len2):
res = res + str(temp[j])
if int(res) == Init_int: # Find alphabetic minimum
return FianlWays[i]
## Start DFS processing
class Solutions:
def DFS(self):
# Sets the deepest depth of DFS
self.MaxDeep = 4 # This data is particularly effective and helps to improve the execution speed of the algorithm.
# Query the elements of the target area
targetdict = findTarget(subData)
# Store final results
self.FinalWays = []
for candicate_i in range(3):
## 1 initially select the initial target elements (the largest number)
if candicate_i == 0:
label = targetdict['max'][0]
label_num = targetdict['max'][1]
elif candicate_i == 1:
label = targetdict['mid'][0]
label_num = targetdict['mid'][1]
elif candicate_i == 2:
label = targetdict['min'][0]
label_num = targetdict['min'][1]
## 2 next, is it going to rotate?
self.ways = []
for dir_i in range(8):
step = [dir_i]
self.dfs(subData,label,label_num,dir_i,step)
## 3 find the scheme with the smallest length and save it
if len(self.ways)>0:# It indicates that a suitable scheme has been found
# Find the scheme with the smallest length and save it
Ways = findWays(self.ways)
self.FinalWays.append(Ways)
break
# Process the saved scheme
if len(self.FinalWays)>0: # It shows that there is a feasible scheme
# Output according to the output requirements.
return findWays(self.FinalWays)
else:
# It indicates that there is no feasible scheme
return "No Solution"
def dfs(self,data,label,label_num,dir,step):
# Set the rotation and return the rotated matrix and the dictionary of the target area
new_subData, new_targetdict = Rotation(data, dir)
new_label = new_targetdict['max'][0]
new_label_num = new_targetdict['max'][1]
# What is terminated or not: 1:
if new_label == label:
if new_label_num == 8:# The label does not change, and the target area is the same element
self.ways.append([step,label])# Save the current scheme and label
return
else:
return
# Termination 2: if the step exceeds the expected depth, an error is reported and returned
if len(step) > self.MaxDeep:
return
## 2. If the termination conditions are not met, continue to execute
if new_label == label and new_label_num>=label_num: # It is valid only when the target element remains unchanged and the number does not decrease
# Proceed to the next dfs cycle
for dir_i in range(8):
new_step = []
new_step.append(dir_i)
for step_i in step:
new_step.append(step_i)
# Ensure that the order cannot be changed, otherwise the order will be wrong when the final output is made
new_step.append(dir_i) # Add at tail
# And remove the data of the head
new_step.pop(0)
self.dfs(new_subData,new_label,new_label_num,dir_i,new_step)
else:
return
return
## First, welcome the data and store the data in a 7 * 7 matrix
data = []
while True:
n = input().strip()
if len(n) == 1 and int(n)==0:
break
# Stored in the matrix
temp = list(map(int,n.strip().split(' ')))
data.append(temp)
# print(data)
# Number of case s
N = len(data)
# Set operation flag
action = {0:['A'],1:['B'],2:['C'],3:['D'],4:['E'],5:['F'],6:['G'],7:['H']}
for casei in range(N):
subData = data[casei]
# Convert data to matrix
subData = data2Matrix(subData)
test = Solutions()
ans = test.DFS()
# Print
res = ''
for i in ans[0]:
res = res + action[i][0]
print(res)
print(ans[1])
Input:
1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 0
Output:
AC 2 DDHH 2