12 kinds of ranking of postgraduate entrance examination are listed
Bubble sorting
- Compare adjacent elements. If the first is larger than the second, exchange them.
- Do the same for each pair of adjacent elements, starting from the first pair to the last pair. After completion, the last element will be the largest element.
- Repeat the above steps for all elements except the sorted ones.
- Continue to repeat the above steps for fewer and fewer elements until no pair of numbers need to be compared or exchanged
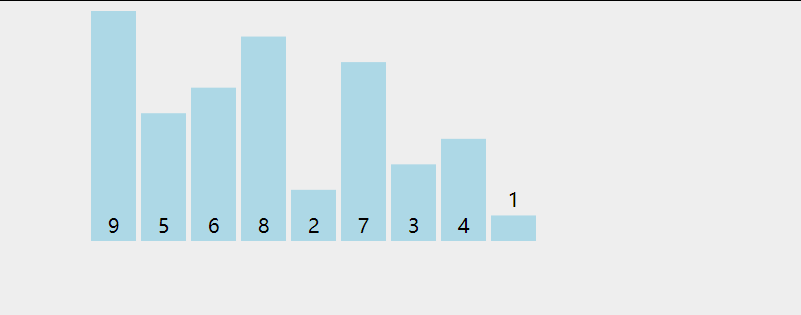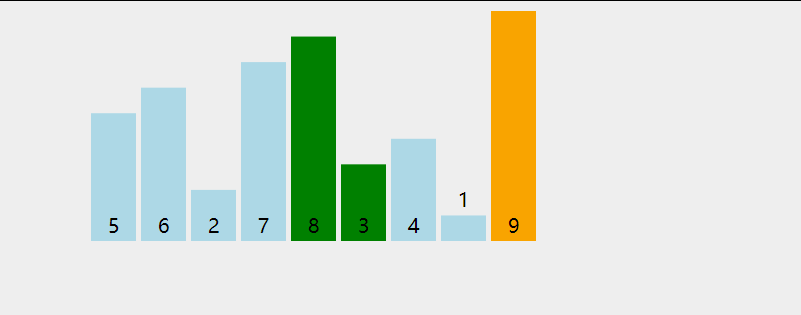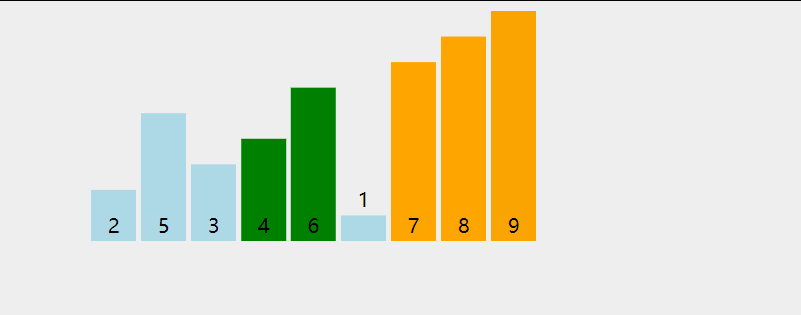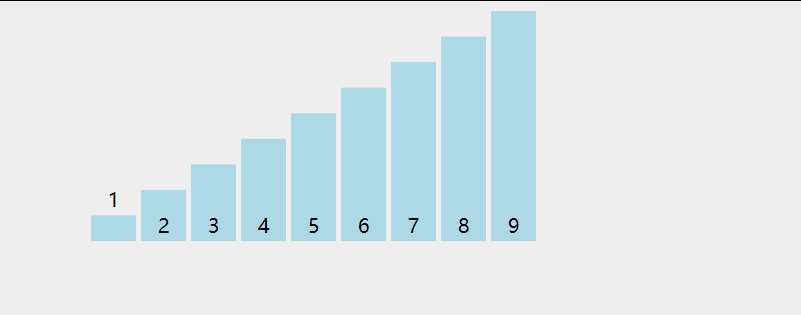
void bubbleSort(int a[], int n)
{
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < n - i - 1; ++j)
{
if (a[j] > a[j + 1])
{
swap(a[j], a[j + 1]);
}
}
}
}
Select sort
-
Find the smallest (large) element in the unordered sequence and store it at the beginning of the sorted sequence.
-
Continue to find the smallest (large) element from the remaining unordered elements, and then put it at the end of your sorted sequence.
-
And so on until all elements are sorted
void selectionSort(int a[], int len)
{
int min;
for (int i = 0; i < len - 1; i++)
{
min = i;
for (int j = i + 1; j < len; j++)
{
if (a[j] < a[min])
{
min = j;
}
}
swap(a[i], a[min]);
}
}
Insert sort
- Starting with the first element, the element can be considered to have been sorted.
- Take out the next element and scan forward from the back in the sorted element sequence.
- If the element (sorted) is larger than the new element, the element moves to the next position.
- Repeat step 3 until you find a location where the sorted element is less than or equal to the new element.
- Insert the element into the corresponding position.
- Repeat 2 ~ 5.
void InsertSort(int a[], int n)
{
for (int i = 1; i < n; i++)
{
if (a[i] < a[i - 1])
{
int val = a[i];
int j = i - 1;
a[j + 1] = a[j];
while (j > 0 && val < a[j - 1])
{
a[j] = a[j - 1];
j--;
}
a[j] = val;
}
}
}
Quick sort
- Select the first number as the standard.
- Exchange the data smaller than the benchmark to the front and the data larger than the benchmark to the back
- Repeat for the space on the left and the space on the right until there is only one number in each interval
void QuickSort(int a[], int left, int right)
{
if (left >= right)
return;
int begin = left;
int end = right;
//keyi is set on the right. You need to start from the left
int keyi = end;
int key = a[keyi];
while (begin < end)
{
//Because we line up from childhood
//Start on the left and find the big one
while (begin < end && a[begin] <= key)
begin++;
a[end] = a[begin];
//Start on the right and look for the small
while (begin < end && a[end] >= key)
end--;
a[begin] = a[end];
}
a[end] = key;
QuickSort(a, left, end - 1);
QuickSort(a, end + 1, right);
}
Heap sort
- If you want to sort from small to large, create a large number, and the root node is larger than the left and right subtrees.
- The root node is exchanged with the last element, and the number of elements in the tree is reduced by 1.
- Repeat 1 ~ 2 until there is only one element left.

void HeadAdjust( ElemType A[] , int k , int len){
//The function HeadAdjust continues to adjust the subtree with element K as the root
A[0] = A[k]; //A[0] staging root node of subtree
for(i = 2*k ; i <= len ; i*=2){ //Filter down along child nodes with larger key s
if( i < len && A[i] < A[i+1])
i++; //Take the subscript of the child node with larger key
if(A[0] >= A[i])
break; //End of filtering
else{
A[k] = A[i]; //Adjust A[i] to parent node
k = i; //Modify the k value to continue filtering down
}
}
A[k] = A[0]; //The value of the filtered node is placed in the final position
}
void BuildMaxHeap( ElemType A[] , int len){
for(int i = len/2 ; i>0 ; i-- )
HeadAdjust(A ,i , len); //Adjust the heap repeatedly from i = [n/2]
}
void HeapSort( ELemType A[] , int len){
//Sorting algorithm
BuildMaxHeap(A , len); //Build heap
for( i = len/2 ; i >0 ;i--){ //n-1 times of exchange and key heap process
Swap(A[i] , A[1]); //Output stack top element (exchange with stack bottom)
HeadAdjust(A , 1 , i-1); //Adjust, adjust the remaining i-1 elements into a heap
}
}
Count sort
- Find the largest and smallest elements of the array to be sorted
- Count the number of each element with value i in the array and store it in the i-min item of array c
- Save the value of subscript + min to the original array according to the number in array c.
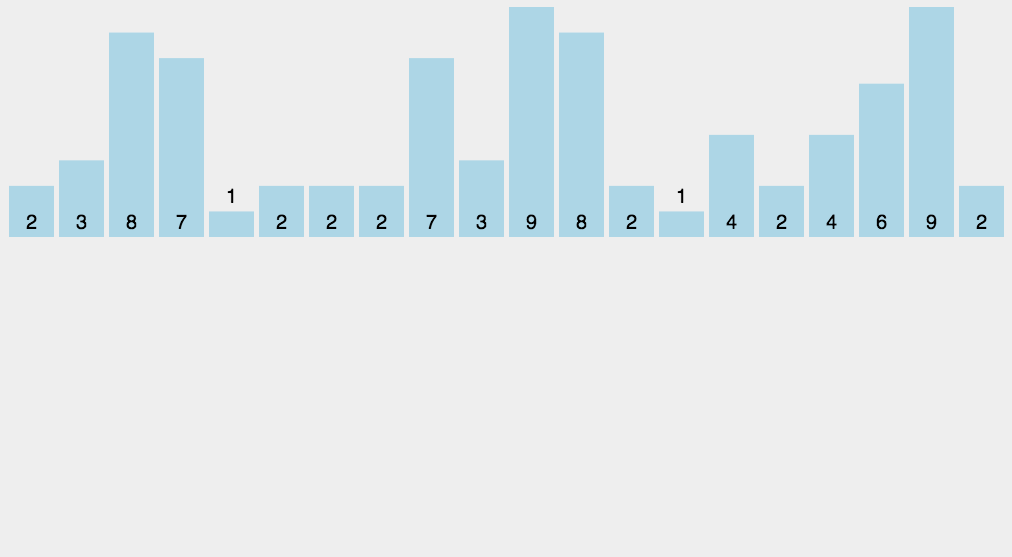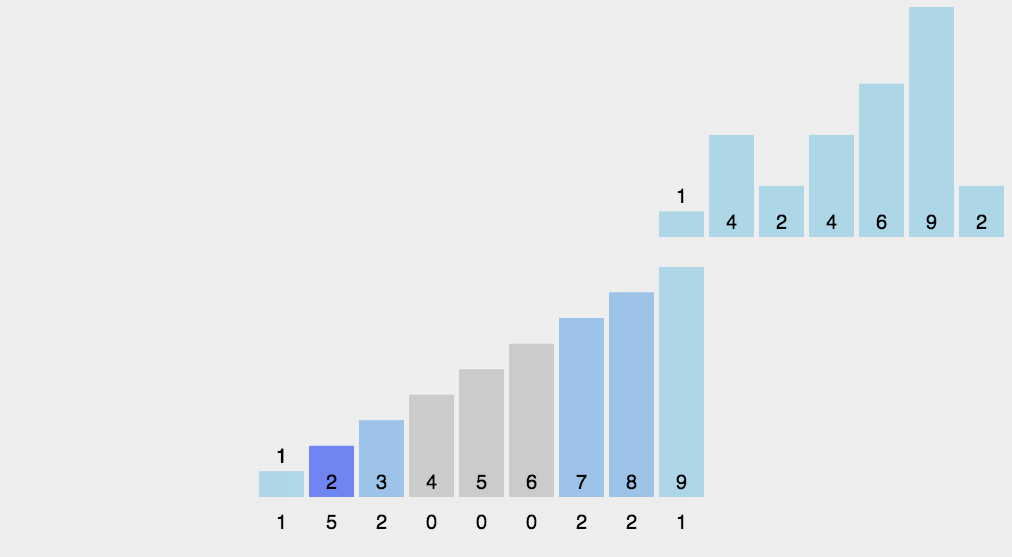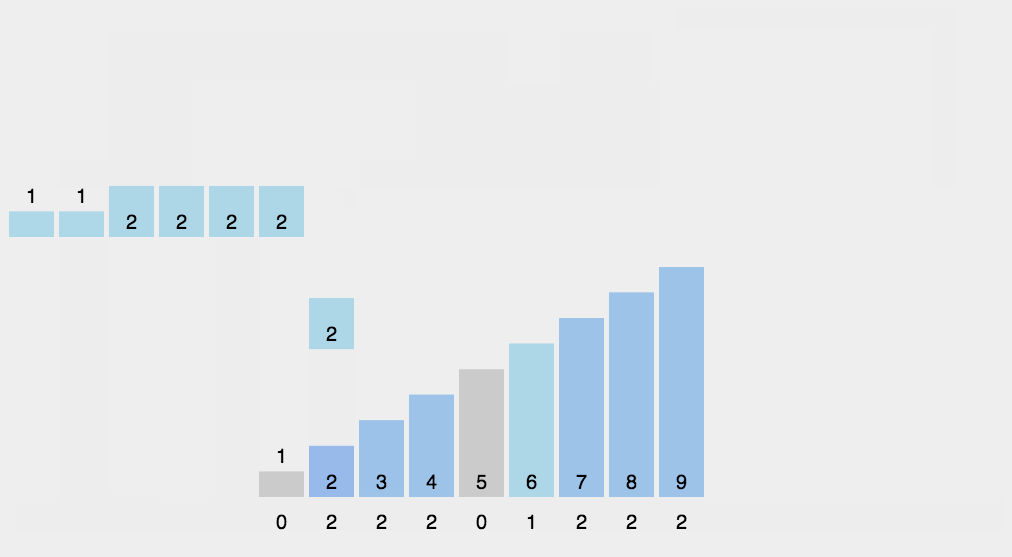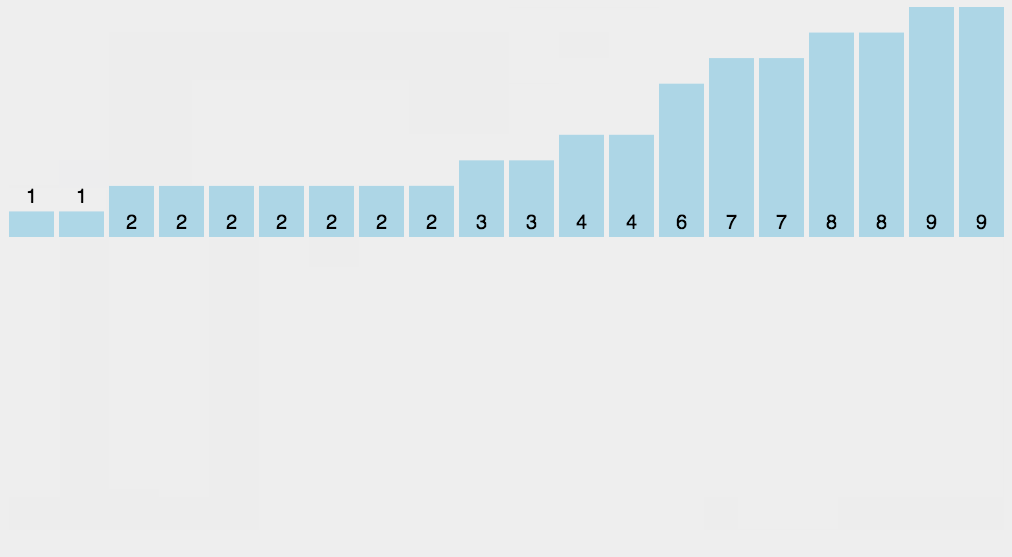
void CountSort(int a[], int len)
{
int max = a[0];
int min = a[0];
for (int i = 0; i < len; i++)
{
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
int l = max - min;//Calculates the difference between the maximum and minimum values of the array
int* count_a = new int[l + 1];
for (int i = 0; i < l + 1; i++)
{
count_a[i] = 0;
}
for (int i = 0; i < len; i++)
{
count_a[a[i] - min]++;//Number of statistical elements
}
int j = 0;
for (int i = 0; i < len; i)
{
while (j <= l && count_a[j])
{
count_a[j]--;
a[i] = j + min;
i++;
}
j++;
}
}
Bucket sorting
- Set a quantitative array as an empty bucket;
- Traverse the input data and put the data into the corresponding bucket one by one;
- Sort each bucket that is not empty;
- Splice the ordered data from a bucket that is not empty.
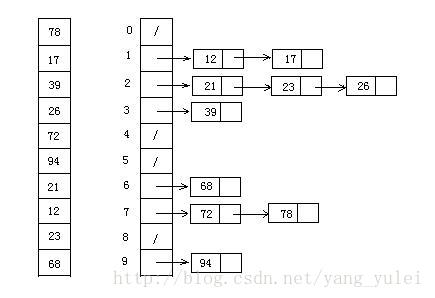
Cardinality sort
- Gets the maximum number in the array and the number of bits.
- arr is the original array, and each bit is taken from the lowest bit to form a radius array.
- Count and sort the radix (using the characteristics that count sorting is suitable for a small range of numbers).
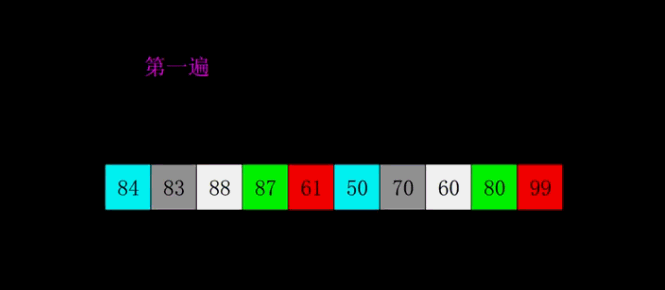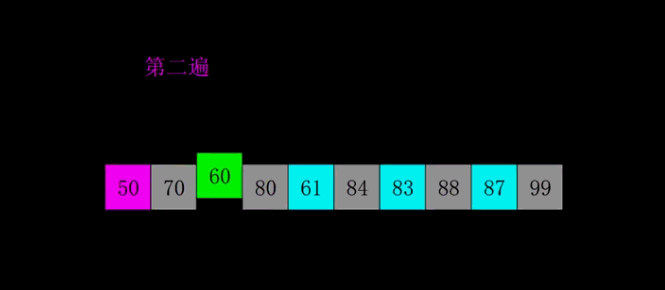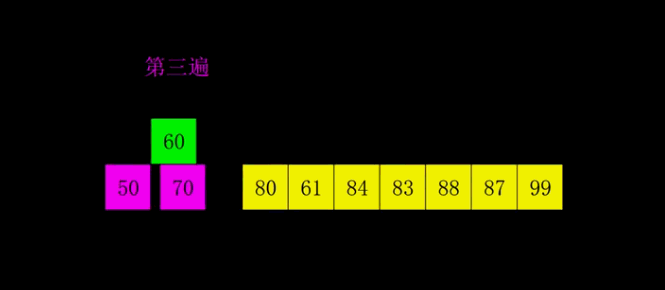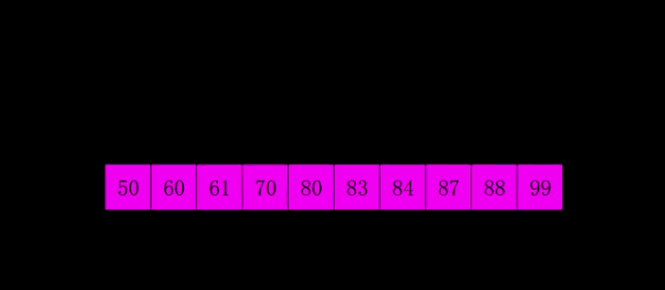
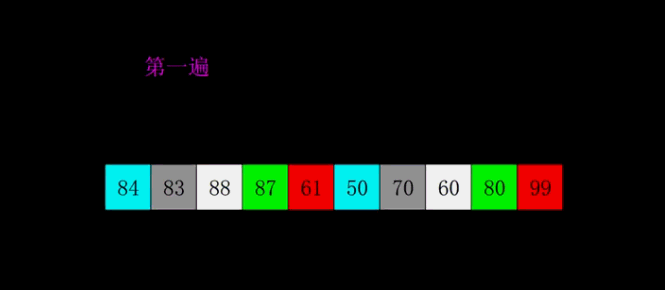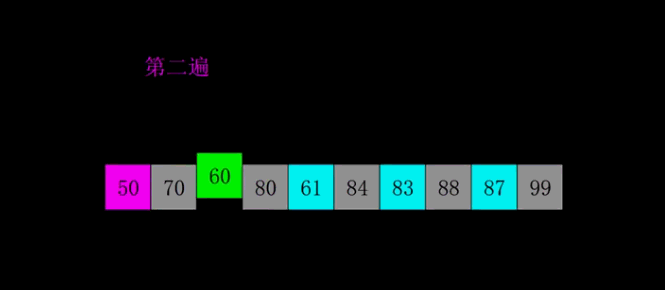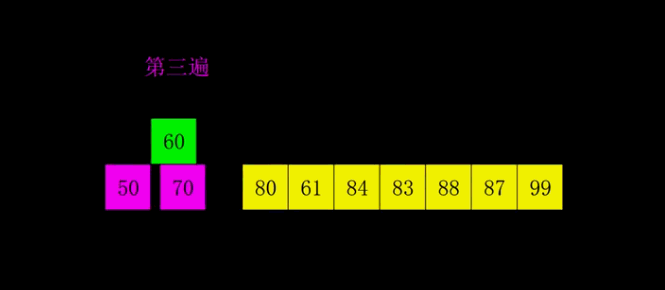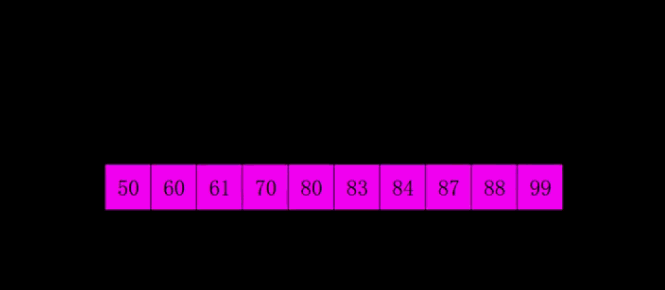
Shell Sort
- Select an incremental sequence t1,t2,..., tk, where ti > TJ, tk = 1.
- Sort the sequence k times according to the number of incremental sequences k
- According to the corresponding increment ti, the sequence to be sorted is divided into several subsequences with length m, and each sub table is directly inserted and sorted.
void ShellSort(int* a, int n)
{
printf("Original array->", gap);
PrintArray(a, n);
int gap = n;//interval
while (gap > 1)
{
gap = gap / 3 + 1;//Ensure that the last trip must be 1
for (int i = 0; i < n - gap; i++)
{
int end = 0;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
printf("gap:%d->", gap);
PrintArray(a, n);
}
}
Merge sort
- The input sequence with length n is divided into two subsequences with length n/2;
- The two subsequences are sorted by merging;
- Merge two sorted subsequences into a final sorting sequence.
ElemType *B=(ElemType *)malloc((n+1)*sizeof(ElemType)); //Auxiliary array B (dynamically allocate memory)
void Merge(ElemType A[],int low,int mid,int high){
//The two segments A[low... Mid] and A[mid+1... high] of table A are ordered respectively, and they are combined into an ordered table
for(int k=low;k<=high;k++) B[k]=A[k];
//Copy all elements from A to B
for(int i=low,j=mid+1,k=i;i<=mid&&j<=high;k++){
//k is the subscript counter of the merged array
if(B[i]<=B[j]) //Compare the elements in the left and right paragraphs of B
A[k]=B[i++]; //Copy the smaller value into A
else
A[k]=B[j++];
}
while(i<=mid)
A[k++]=B[i++]; //If the first table is not detected, copy the rest directly
while(j<=high)
A[k++]=B[j++]; //If the second table is not detected, copy the rest directly
}
void MergeSort(ElemType A[],int low,int high){
if(low<high){
int mid=(low+high)/2;//Divide two subsequences from the middle
MergeSort(A,low,mid);//Recursively sort the left subsequence
MergeSort(A,mid+1,high);//Recursively sort the right subsequence
Merge(A,low,mid,high);//Merge
}
}
Binary Insertion Sort
void InsertSort(ElemType A[] , int n){
int i , j ,high , mid , low;
for(i =2 ; i < n ;i++){
A[0] = A[i];
low = 1;
high = i-1;
while(low <= high){
mid = (low + high)/2;
if(A[mid] > A[0])
high = mid-1;
else
low = mid+1;
}
for( j = i-1 ; i>= high+1 ; --J)
A[j+1] = A[j];
A[high+1] = A[0];
}
}
Simple sort
//Sequential table form
void SelectSort( ElemType A[] , int n ){
for( int i = 0 ; i < n ; i++){
min = i; //Record minimum element position
for( j = i+1 ; j < n ; j++){ //Find the smallest element from A []
if( A[j] < A[min])
min = j; //Update minimum element location
}
if(min = !i )
Swap( A[i] , A[min]); //The encapsulated swap function moves elements three times at a time
}
}
//Linked list structure
void selectSort_LinkList(LinkList &L){
Lnode *h = L , *p, *q , *s , *r;
while( p != NULL){
p = s = h ; //Pointers S and R memorize the maximum node and its precursor, p is the working node and q is the precursor
q = r= NULL;
while( p != NULL){
if( p->data > s->data){
s = p;
r = q; //Find a bigger memory of him and its precursors
}
q = p;
p = p->nexr; //Keep looking
}
if( s == h)
h = h->next; //The largest node is at the front end of the original linked list
else
r->next = s->next;
s->next = L; //The maximum node is in the original linked list
L = s; //The node s is inserted into the front end of the result chain
}
}
algorithm
Bidirectional Bubble Sort
Scan alternately from both positive and negative directions
void BubbleSort(int A[] , int n){
//Two way bubbling sorting, alternating the bubbling process in both positive and negative directions
int low = 0 , hight = n-1;
int temp = 0 ;
int flag = true; //Whether the marked elements are exchanged
while( low < hight && flag){
flag = false;
for( int i = low ; i < n ; i++){
if(A[i] > A[i+1]){ //Bubbling from front to back
temp = A[i+1]; //Reverse order occurs
A[i+1] = A[i];
A[i] = temp;
flag = true;
}
}
hight--; //Update upper bound
for( int j = hight ; j < n ; j--){
if(A[j] < A[j-1]){ //Reverse order occurs
temp = A[j-1];
A[j-1] = A[j];
A[j] = temp; //exchange
flag = true; //Set flag
}
}
low++; //Modify lower bound
}
}
Swap odd numbers before even numbers
Table A is basically ordered and stored sequentially, and each element is A different shaping element
void Move(int A[] , int n){
//Divide the odd and even numbers of basically ordered table A once
int i = 0 , j = n -1 , temp = 0; //i represents the subscript of the left even element, and j represents the subscript of the right odd element
while( i < j){
while( i<j && A[i] % 2 != 0) //Even function found
i++;
while( i < j && A[j] %2 != 1) //Odd function found
j--;
if( i < j ){ //Exchange element
temp = A[i];
A[i] = A[j];
A[j] = temp;
}
i++;
j--;
}
}
Fast scheduling algorithm for random hub values
int Partition_random(int A[] , int n ,int low , int high){
int rand_Index = low + rand()%(high - low+1); //Find the random value
swap(A[rand_Index] , A[low]); //Swap hub values to the first element
int pivot = A[low]; //Set the first value as the pivot value
int i = low; //Make all elements in table a [low... I] smaller than pivot, and the initial table is empty
for( int j = low +1 ; j <= high ; j++){ //Start with the second element and look for elements smaller than the benchmark
if(A[j] < pivot) //When you find it, switch to the front
swap(pivot , A[j]);
}
swap(A[i] , A[low]); //Insert datum element into final position
return i; //Returns the position of the base element
}
Find the k-th value
void kth_Elem( int A[] , int low , int high , int k){
int temp_low = low;
int temp_high = high;
int pivot = A[low];
while(low < high){
while( low < high && A[high] <= pivot)
A[low] = A[high];
high--;
while( low < high && A[low] >= pivot )
A[high] = A[low];
low++;
}
a[low] = pivot;
//That's the quick sort part
if( k == low)
return low;
if(low >k) //Backward recursive search
return kth_Elem(A , temp_low , low-1 , k) ;
else
return kth_Elem(A , low+1 , temp_high , k);
}
The minimum difference between the number of elements in two sets and the minimum difference between the sum of elements
Two disjoint subsets A1 and A2, the element difference between them is | n1 - n2 | and the element sum difference is | S1 - S2|
int setPartition( int A[] , int n){
int flag = 1,low = 0, low0 = 0 , high = n-1 , high0 = n-1 , k = n/2;
int pivotkey;
int s1 = 0 , s2 = 0;
while(flag){
pivotkey = A[0]; //Select the pivot
while( low < high ){ //Divide based on pivot
while( low < high && A[high] >= pivotkey )
high --;
if( high != low)
A[low] = A[high];
while( low < high && A[low] <= pivotkey)
low ++;
if( high != low)
A[high] = A[low];
}
A[low] = pivotkey;
if( low == key) //The grouping is completed and the algorithm ends
flag = 0;
if( low > key){ //The pivot and subsequent elements belong to A2. Continue to divide the elements before i
low0 = ++low;
high = high0;
}
else{ //Pivot and previous elements belong to A1
high0 = --high;
low = low0;
}
}
for(1 = 0 ; 1 < key ; 1++){
s1 += A[i];
}
for( i = k ; i < n ; k++){
s2 += A[i];
}
return s2 - s1;
}
Dutch flag issue
For the color block composed of red, white and green, the algorithm with complexity of o(n) is compiled to make it orderly arranged into the Dutch flag
typedef enum[RED , WHITE , BLUE] color; //Set enumeration array
void Flag_Arrange( color a[] , int n){
int i =0 ,j =0 , k = n-1;
while( j <= k )
switch(a[j]){ //Judge color
case RED : swap(a[i] , a[j]) ; i++; break;
case WHITE : j++ ; break;
case BLUE : swap(a[j] , a[k]); k--;
//Blue, then swap with k
//There is no j + + statement here to prevent a[j] from being blue after the exchange
}
}
Judge whether the data sequence constitutes a small root heap
bool IsMinHeap( ElemType A[] , int len){
if(len%2 == 0){ //If it is even, there is a single branch node
if( A[len/2] > A[len]) //Judge single branch node
return false;
for( i = len/2 - 1 ;i >=1 ; i--){
if( A[i] > A[2*i] || A[i] > A[2*i+1])
return false; //Judge all double branch nodes
}
}
else{ //len is odd,
for( i =len/2 ; i>= 1 ; i--){ //Judge all double branch nodes
if( A[i] > A[2*i] || A[i] > A[2*i+1])
return false;
}
return true;
}
}