preface

The one-dimensional prefix sum is introduced earlier. The two-dimensional prefix sum is the online upgrade of the one-dimensional prefix sum. The one-dimensional prefix sum is reflected in the array, while the two-bit prefix sum is reflected in the matrix.

1, What are two-dimensional prefixes and?

Based on the one-dimensional prefix sum, what we seek now is the sum of the number of any submatrix in the matrix, so we can use the two-dimensional prefix sum to solve this problem.

2, 2D prefix and explanation

introduce

For a matrix
For example: define a matrix g[n][m]

const int n=3,m=4;
int g[n][m]={{1,5,6,8},{9,6,7,3},{5,3,2,4}};

g[n][m]
1   5   6   8
9   6   7   3
5   3   2   4

 (1) Find matrix(1,1)reach(2,2)And
 (2) Find matrix(0,1)reach(1,3)And

The easiest thing to think of is violent enumeration
Namely:
Question (1) 6 + 7 + 3 + 2 = 18
Question (2) 5 + 6 + 8 + 6 + 7 + 3 = 35
Its complexity is O(nm). If the matrix is short, it's OK, but when the data is too large, this method is somewhat time-consuming. Therefore, we introduce two-dimensional prefix and sum to reduce its complexity.

thinking

If we take this 3 * 4 matrix as a large rectangle
For problem (1), we can have another solution

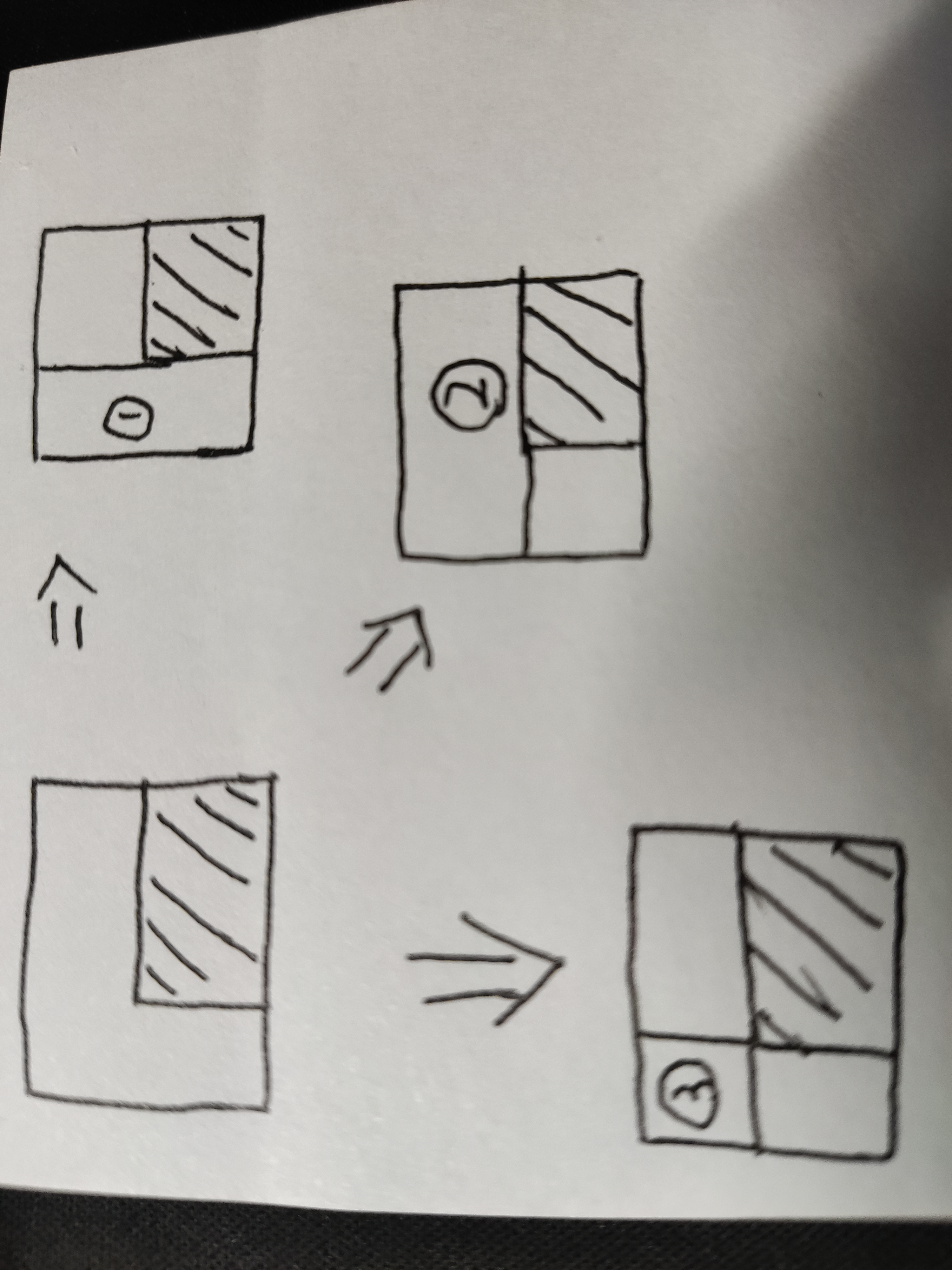
< < let's live and see. I haven't understood the picture for the first time > >
(shadow is required)
The solution is: the shadow = large rectangle - (1) - (2) + (3);
Combined with g[n][m] matrix, we further analyze
Find the matrices g[1],g[2],g[3]

matrix g[1]                  
1   5   6   
9   6   7   
5   3   2   

matrix g[2]     matrix g[3]
1            1   5   6   
9 
5

problem(1)  It can be solved as follows: g[1]-g[2]-g[3]+1
 The question now is how to sum the matrices
 We introduce the two-dimensional prefix and sum[i][j]
sum[i][j]Is from(0,0)reach(i,j)Matrix sum of

That's a better solution
Question (1)=sum[3][3]-sum[2][0]-sum[0][2]+sum[0][0];
sum[n][m] can be obtained from g[n][m]

sum[n][m]
1   6   12   20
10  21  34   45
15  29  44   59

Question (1) = 44-15-12 + 1 = 18 = 6 + 7 + 3 + 2

Expand your thinking and broaden your horizons
 By the right question(1)The solution can be inferred
(set up sum[x1,y1][x2,y2]equivalent
 From( x1,y1)To( x2,y2)(and)

sum[x1,y1][x2,y2]
=sum[x2][y2]-sum[x2][y1-1]-sum[x1-1][y2]+sum[x1-1][y1-1]

The code implementation is as follows (example):

#include<bits/stdc++.h>
using namespace std;
const int n=3,m=4;
int g[n][m]={{1,5,6,8},{9,6,7,3},{5,3,2,4}};
int sum[n][m];
void pre_sum()   //Preprocessing generates two-dimensional prefixes and
{
	sum[0][0]=g[0][0]; //first
	for(int i=1;i<n;i++)
		sum[i][0]=sum[i-1][0]+g[i][0];  //First column
	for(int j=1;j<m;j++)
		sum[0][j]=sum[0][j-1]+g[0][j];  //first line
	for(int i=1;i<n;i++)
		for(int j=1;j<m;j++)
	sum[i][j]=g[i][j]+sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1];
}
int get_sum(int x1,int y1,int x2,int y2)
{
	if(!x1&&!y1)  return sum[x2][y2];
	if(!x1)    return sum[x2][y2]-sum[x2][y1-1];
	if(!y1)    return sum[x2][y2]-sum[x1-1][y2];
	return sum[x2][y2]-sum[x2][y1-1]-sum[x1-1][y2]+sum[x1-1][y1-1];
}
int main()
{
	pre_sum();
	cout<<get_sum(1,1,2,2)<<""<<endl<<get_sum(0,1,1,3);
	return 0;
}

explain

Since sum [] [] is a two-dimensional array,
Therefore, the boundary should be specified first, and then the sum [] [] array should be preprocessed

void pre_sum()   //Preprocessing generates two-dimensional prefixes and
{
	sum[0][0]=g[0][0]; //first
	for(int i=1;i<n;i++)
		sum[i][0]=sum[i-1][0]+g[i][0];  //First column
	for(int j=1;j<m;j++)
		sum[0][j]=sum[0][j-1]+g[0][j];  //first line
	for(int i=1;i<n;i++)
		for(int j=1;j<m;j++)
	sum[i][j]=g[i][j]+sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1];
}

First of all, there must be no problem with the former sum[0][0]=g[0][0]
The following two for statements define the boundary of sum in advance

sum Specified boundary
1   6   12   20
10
15

The method of defining the boundary of two-dimensional prefix and is the same as that of one-dimensional prefix and
Then it is quite simple to find sum[i][j] according to the boundary

for(int i=1;i<n;i++)
	for(int j=1;j<m;j++)
		sum[i][j]=g[i][j]+sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1];

Handle custom function get_ When sum(), return three special cases first
No matter how common the rule of return is, it's easy to understand. I won't say much (i.e. lazy)

summary

The two-dimensional prefix and the one-dimensional prefix are not difficult to understand. It may be easier to imagine a graph and use a graph to understand it.