Preorder traversal of binary tree

Title Description

Give you the root node of the binary tree, root, and return the preorder traversal of its node value.

Example 1:

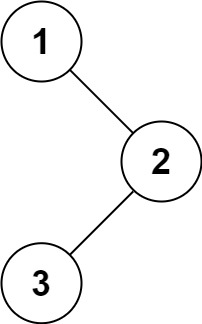
Input: root = [1,null,2,3]
Output:[1,2,3]

Example 2:

Input: root = []
Output:[]

Example 3:

Input: root = [1]
Output:[1]

Method 1: recursion

For tree traversal, recursive method is always the simplest.

Pre order traversal: Root - > left subtree - > right subtree.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        
        preOrder(ans, root);
        return ans;
    }

    private void preOrder(List<Integer> ans, TreeNode root) {
        if (root!=null) {
            ans.add(root.val);
            preOrder(ans, root.left);
            preOrder(ans, root.right);
        }
    }
}

Method 2: iteration

​ We can also use the iterative method to implement the recursive function of method 1. The two methods are equivalent. The difference is that a stack is implicitly maintained during recursion, and we need to explicitly simulate this stack during iteration. The rest of the implementation and details are the same. For details, please refer to the following code.

​ Idea: first traverse the root - > left subtree - > right subtree of binary tree

• For each node, we go all the way to the left
• Then return to the previous node
• Then traverse its right.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        while (root!=null || !stack.isEmpty()) {
            while (root!=null) {
                ans.add(root.val);
                stack.add(root);
                root = root.left;
            }
            root = stack.pop();
            root = root.right;
        }
        return ans;
    }
}

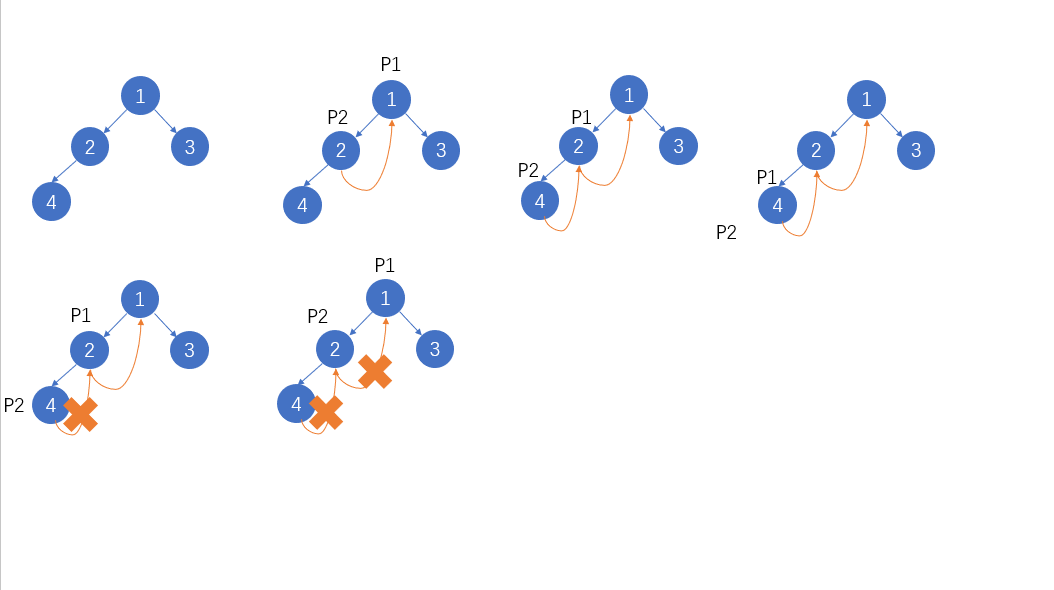
Method 3: Morris traversal

The core idea of Morris traversal is to reduce the space overhead by using a large number of free pointers of the tree. The pre order traversal rules are summarized as follows:

1. Create a new temporary node and make it root;
2. If the left child node of the current node is empty, add the current node to the answer and traverse the right child node of the current node;
3. If the child node in the current child tree is not found in the current child tree, if the child node is not found in the current child tree:
   • If the right child node of the predecessor node is empty, set the right child node of the predecessor node as the current node. Then add the current node to the answer and update the right child node of the precursor node to the current node. The current node is updated to the left child of the current node.
   • If the right child node of the predecessor node is the current node, reset its right child node to null. The current node is updated as the right child node of the current node.
4. Repeat steps 2 and 3 until the traversal is complete.

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        if (root == null) {
            return res;
        }

        TreeNode p1 = root, p2 = null;

        while (p1 != null) {
            p2 = p1.left;
            if (p2 != null) {
                while (p2.right != null && p2.right != p1) {
                    p2 = p2.right;
                }
                if (p2.right == null) {
                    res.add(p1.val);
                    p2.right = p1;
                    p1 = p1.left;
                    continue;
                } else {
                    p2.right = null;
                }
            } else {
                res.add(p1.val);
            }
            p1 = p1.right;
        }
        return res;
    }
}