The spanning tree of   graph is the minimum connected subgraph of graph, which contains all vertices in the graph, but only the number of edges 1 less than the number of vertices. No matter how small the number of edges is, it will not be connected. If there is one more edge, there will be multiple paths between vertices. The tree with the smallest sum of the weights of the edges in the spanning tree is called the minimum spanning tree. Minimum spanning tree has practical application and significance. For example, if the weight corresponds to the distance, the corresponding distance is the shortest and the construction cost is the smallest.
  how to find a minimum spanning tree?
  so far, in memory of this great scientist, prim, we call his algorithm for finding the minimum spanning tree prim algorithm, also known as prim algorithm.
   the core theorem of the algorithm is: divide the vertices in the graph into two sets, then among the edges connecting the two vertex sets, the edge with the smallest weight must appear in the minimum spanning tree.
  according to this theorem, we can build the edges of the minimum spanning tree one by one from nothing. The two vertex sets are the vertices in the established MST and the vertices that do not enter the MST. MST: minimal spanning tree.
  thank Mr. bilibi lazy cat for his wonderful explanation.
  otherwise, the core of this algorithm is really hard to understand. Every line of code in the textbook is recognized, and it's a mess when connected. Know why, then, it's easy to know.
   the graph is stored by the adjacency matrix and gives all the information of the graph. MST is stored with an edge set array. The so-called edge set array is to establish a corresponding structure variable for the edge, including the two vertices and weights of the edge. All edges form an array of edges and give the information of all edges in the graph. MST can directly output the information of all edges.
  function primSolutionMST: prim algorithm solution establishes the minimum spanning tree.
   source file code of main function:

#include<iostream>
#include<stdio.h>
using namespace std;
#define MAXVERTEX 15
#define INFINI 65555

struct GraphAdjaMatrix {
	char vertexes[MAXVERTEX];
	int edges[MAXVERTEX][MAXVERTEX];
	int numVertexes;
	int numEdges;
};

struct Edge {
	int indexA;
	int indexB;
	int weightAB;
};

struct GraphEdgeSetArray {
	int vertexNum;
	int edgeNum;
	char vertexes[MAXVERTEX];
	Edge edges[MAXVERTEX];
};

extern void createGraphAdjMatrix(GraphAdjaMatrix &graphAdjMatrix,
			int numVertexes,int numEdges,int edges[][6],char vertexes[]);
extern void dispalyGraphAdjMatrix(GraphAdjaMatrix &graphAdjMatrix);
extern void primSolutionMST(GraphAdjaMatrix& graphAdjMatrix,
	GraphEdgeSetArray & graphMST,int indexStart);

int main() {
	GraphAdjaMatrix graphAdjMatrix ;
	int numVertexes = 6, numEdges = 10;
	int edges[][6] = {	{0,34,46,INFINI,INFINI,19},
						{34,0,INFINI,INFINI,12,INFINI},
						{46,INFINI,0,17,INFINI,25},
						{INFINI,INFINI,17,0,38,25},
						{INFINI,12,INFINI,38,0,26},
						{19,INFINI,25,25,26,0} };
	char vertexes[] = {'a','b','c','d','e','f'};

	createGraphAdjMatrix(graphAdjMatrix,numVertexes,numEdges,edges,vertexes);
	dispalyGraphAdjMatrix(graphAdjMatrix);
	cout << endl;

	GraphEdgeSetArray graphMST;
	primSolutionMST(graphAdjMatrix,graphMST,3);

	cout << "its minimal spanning tree is as following :" << endl;
	for (int i = 0; i < graphMST.edgeNum; i++) {
		cout << '(' << graphMST.vertexes[graphMST.edges[i].indexA] << ',';
		cout << graphMST.vertexes[graphMST.edges[i].indexB] << ')';
		cout << graphMST.edges[i].weightAB;
		cout << "          ";
		cout << '(' <<graphMST.edges[i].indexA << ',';
		cout << graphMST.edges[i].indexB << ')';
		cout << graphMST.edges[i].weightAB << endl;;
	}

	return 0;
}

Source file code of each function:

#include<iostream>
#include<stdio.h>
using namespace std;
#define MAXVERTEX 15
#define INFINI 65555

struct GraphAdjaMatrix {
	char vertexes[MAXVERTEX];
	int edges[MAXVERTEX][MAXVERTEX];
	int numVertexes;
	int numEdges;
};

struct Edge {
	int indexA;
	int indexB;
	int weightAB;
};

struct GraphEdgeSetArray {
	int vertexNum;
	int edgeNum;
	char vertexes[MAXVERTEX];
	Edge edges[MAXVERTEX];
};

void createGraphAdjMatrix(GraphAdjaMatrix &graphAdjMatrix,
	int numVertexes, int numEdges, int edges[][6], char vertexes[]) {
	graphAdjMatrix.numVertexes = numVertexes;
	graphAdjMatrix.numEdges = numEdges;
	
	for (int i = 0; i < numVertexes; i++)
		graphAdjMatrix.vertexes[i] = vertexes[i];

	for (int row = 0; row < numVertexes; row++)
		for (int column = 0; column < numVertexes; column++)
			graphAdjMatrix.edges[row][column] = edges[row][column];
}

void dispalyGraphAdjMatrix(GraphAdjaMatrix &graphAdjMatrix) {
	cout << "adjacensy matrix :" << endl;
	int row,column;
	printf("%3c",' ');
	for (row = 0; row < graphAdjMatrix.numVertexes; row++)
		printf("%3c",graphAdjMatrix.vertexes[row]);
	printf("\n");
	for (row = 0; row < graphAdjMatrix.numVertexes; row++) {
		printf("%-3c", graphAdjMatrix.vertexes[row]);
		for (column = 0; column < graphAdjMatrix.numVertexes; column++)
			if (graphAdjMatrix.edges[row][column] == INFINI)
				printf("%3s", "∞");
			else
				printf("%3d",graphAdjMatrix.edges[row][column]);
		cout << endl;
	}
}

void primSolutionMST(GraphAdjaMatrix& graphAdjMatrix,
	GraphEdgeSetArray& graphMST, int indexStart) {

	Edge edgeShortest;

	bool inMST[MAXVERTEX], outOfMST[MAXVERTEX];
	for (int i = 0; i < graphAdjMatrix.numVertexes; i++) {
		inMST[i] = false;
		outOfMST[i] = true;
	}

	inMST[indexStart] = true;
	outOfMST[indexStart] = false;

	graphMST.vertexNum = graphAdjMatrix.numVertexes;
	for (int i = 0; i < graphAdjMatrix.numVertexes; i++)
		graphMST.vertexes[i] = graphAdjMatrix.vertexes[i];
	graphMST.edgeNum = 0;

	int indexInMST, indexOutOfMST;
	while (graphMST.edgeNum <= graphMST.vertexNum - 1) {
		edgeShortest.weightAB = INFINI;
		edgeShortest.indexA = -1;
		edgeShortest.indexB = 0;

		for (indexInMST = 0; indexInMST < graphAdjMatrix.numVertexes; indexInMST++) 
			for (indexOutOfMST = 0; indexOutOfMST < graphAdjMatrix.numVertexes; indexOutOfMST++)
				if ((indexInMST != indexOutOfMST)
					&& (inMST[indexInMST] && outOfMST[indexOutOfMST]) &&
					graphAdjMatrix.edges[indexInMST][indexOutOfMST] < edgeShortest.weightAB) {
					
					edgeShortest.indexA = indexInMST;
					edgeShortest.indexB = indexOutOfMST;
					edgeShortest.weightAB = graphAdjMatrix.edges[indexInMST][indexOutOfMST];
				}

		graphMST.edges[graphMST.edgeNum] = edgeShortest;
		graphMST.edgeNum++;
		inMST[edgeShortest.indexB] = true;
		outOfMST[edgeShortest.indexB] = false;
	}
	graphMST.edgeNum--;
}

The corresponding graph and minimum spanning tree are as follows:



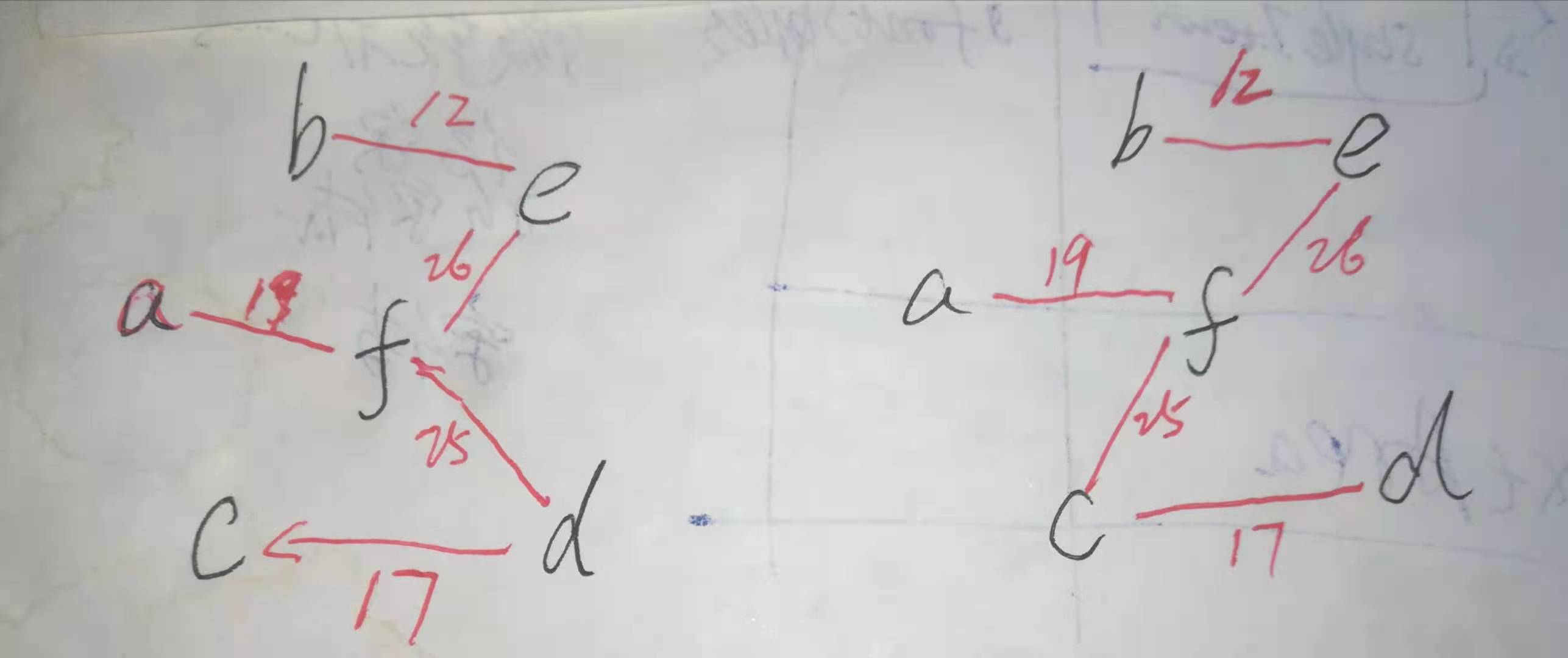
The results given by Mr. bilibnili lazy cat are shown in the screenshot:

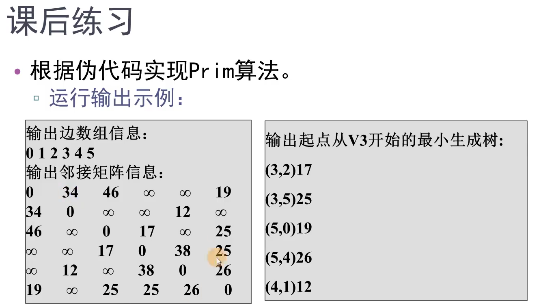
  it can be seen that the minimum spanning tree is different because there are edges with the same weight. But they are all correct, so the minimum spanning tree is not unique.
Thank you for reading.