After reading this article, you can not only learn the algorithm routine, but also win the following topics on LeetCode:
1135. Minimum cost connectivity to all cities (medium)
1584. Minimum cost of connecting all points (medium)
-----------
This is the seventh graph theory algorithm article. First, list the graph theory algorithms I wrote before:
1,Fundamentals of graph theory algorithm
2,Bipartite graph decision algorithm
3,Ring detection and topological sorting algorithm
4,Dijkstra shortest path algorithm
5,Union Find parallel search algorithm
6,Kruskal minimum spanning tree algorithm
Although advanced algorithms such as graph theory algorithm are not difficult, the amount of reading is generally low. I didn't want to write Prim algorithm, but considering the integrity of algorithm knowledge structure, I still want to fill in the pit of Prim algorithm, so that all classical graph theory algorithms are basically perfect.
Prim algorithm and Kruskal algorithm are classic minimum spanning tree algorithms. Before reading this article, I hope you have read the previous article Kruskal minimum spanning tree algorithm , understand the basic definition of minimum spanning tree and the basic principle of Kruskal algorithm, so that you can easily understand the logic of Prim algorithm.
Compare Kruskal algorithm
The minimum spanning tree problem of graph theory is to find several edges from the graph to form a set mst of edges. These edges have the following characteristics:
1. These edges form a tree (the difference between a tree and a graph is that it cannot contain rings).
2. The tree formed by these edges should contain all nodes.
3. The sum of the weights of these edges should be as small as possible.
So what logic does Kruskal algorithm use to meet the above conditions and calculate the minimum spanning tree?
Firstly, Kruskal algorithm uses the greedy idea to meet the problem that the sum of weights is as small as possible:
First, all edges are sorted according to the weight from small to large. Starting from the edge with the smallest weight, select the appropriate edge to join the mst set. In this way, the tree composed of the selected edge is the one with the smallest weight and weight.
Secondly, Kruskal algorithm uses Union find parallel search algorithm To ensure that the selected edges must form a "tree" and will not contain rings or form a "forest":
If the two nodes of an edge are already connected, the edge will make a ring appear in the tree; If the total number of the last connected components is greater than 1, it indicates that a "forest" is formed rather than a "tree".
So, what logic does Prim algorithm use to calculate the minimum spanning tree?
Firstly, Prim algorithm also uses the greedy idea to make the weight of spanning tree as small as possible, that is, the "segmentation theorem", which will be explained in detail later.
Secondly, Prim algorithm is used BFS algorithm idea And visited Boolean arrays avoid forming rings to ensure that the selected edges will eventually form a tree.
Prim algorithm does not need to sort all edges in advance, but uses priority queue to dynamically realize the sorting effect, so I think prim algorithm is similar to Kruskal's dynamic process.
Here is the core principle of Prim algorithm: segmentation theorem.
Segmentation theorem
The term "segmentation" is actually easy to understand, which is to divide a graph into two non overlapping and non empty node sets:
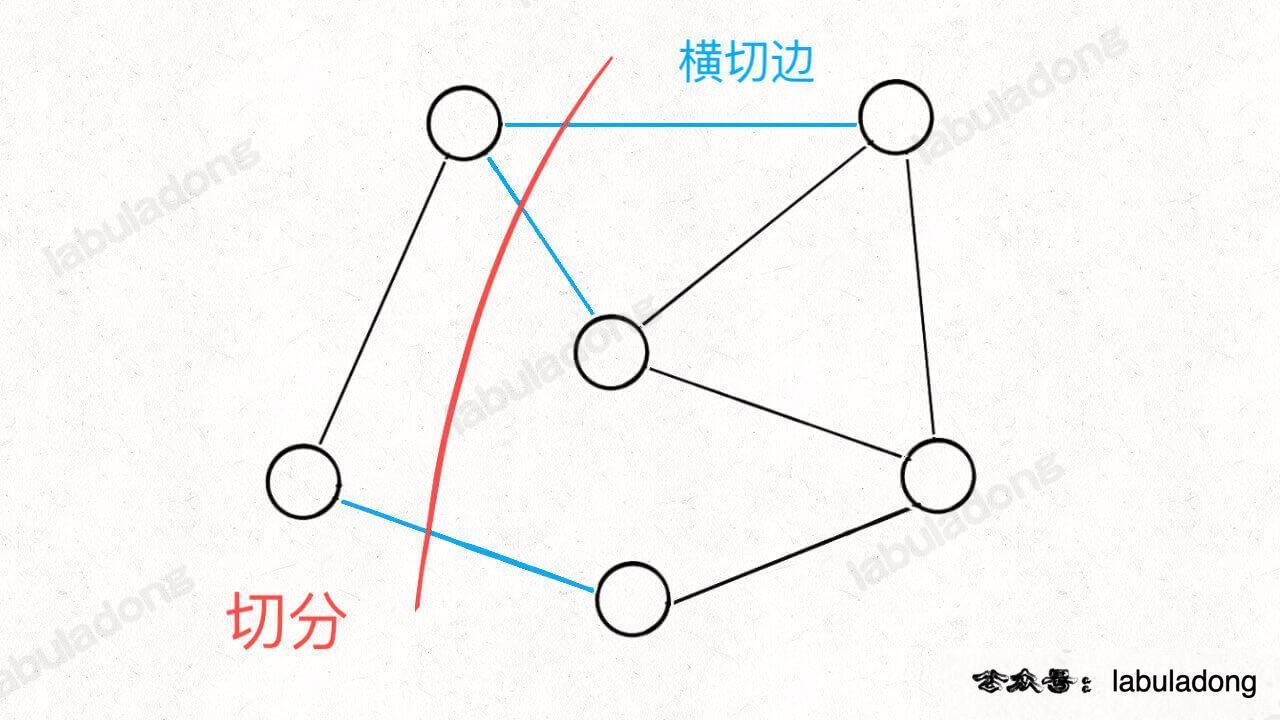
The red knife divides the nodes in the graph into two sets, which is a kind of "segmentation". The edge cut by the red line (marked as blue) is called "crosscutting edge".
PS: remember the meaning of these two professional terms. We will use them frequently later. Don't get confused.
Of course, a picture can certainly have several kinds of segmentation, because according to the definition of segmentation, as long as you can divide the nodes into two parts at one stroke.
Next, we introduce the "segmentation theorem":
For any kind of "segmentation", the "crosscutting edge" with the smallest weight must be an edge constituting the smallest spanning tree.
It should be easy to prove that if there is a minimum spanning tree in a weighted undirected graph, assume that the edge marked in green in the following figure is the minimum spanning tree:
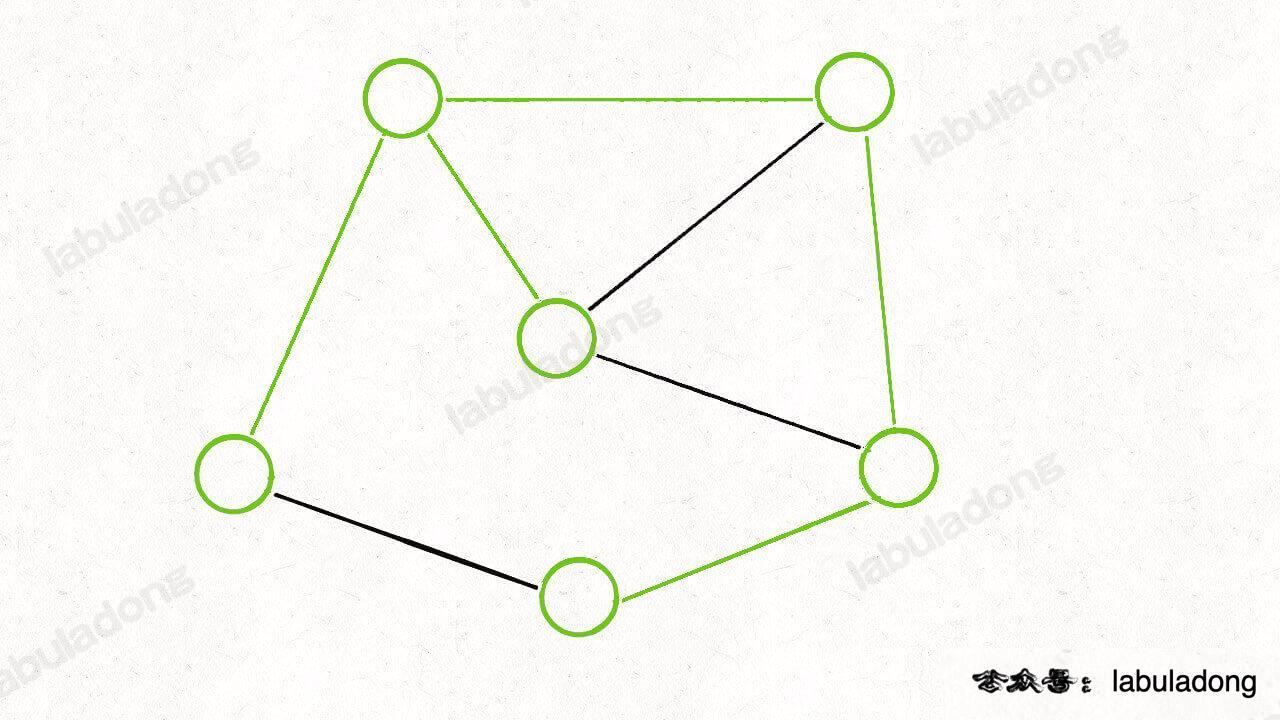
Then, you can certainly find some "segmentation" methods to cut the minimum spanning tree into two subtrees. For example, the following segmentation:
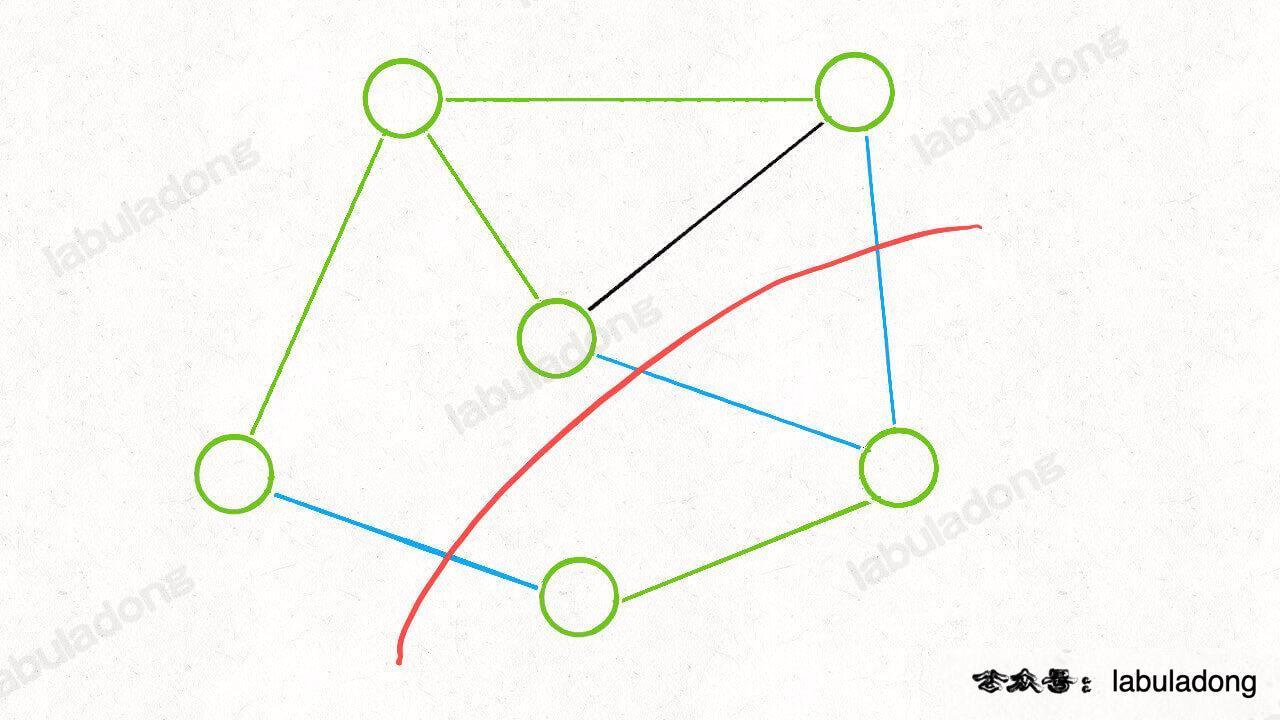
You will find that any blue "crosscutting edge" can connect the two subtrees to form a spanning tree.
So how do you choose to minimize the weight sum of the final spanning tree?
You must choose the "crosscutting edge" with the least weight, right? This proves the segmentation theorem.
As for the segmentation theorem, you can also prove it by counter evidence:
Given the minimum spanning tree of a graph, any "segmentation" must have at least one "cross cutting edge" belonging to the minimum spanning tree.
Assuming that this "crosscutting edge" is not the one with the smallest weight, it means that the weight sum of the smallest spanning tree still has room to be reduced. This is a contradiction. How can the weight sum of the smallest spanning tree be reduced again? So the segmentation theorem is correct.
With this segmentation theorem, you probably have an algorithm idea for calculating the minimum spanning tree:
Since each "segmentation" can find an edge in the minimum spanning tree, I will cut it casually. Each time, I will take out the "crosscutting edge" with the lowest weight and add it to the minimum spanning tree until all the edges constituting the minimum spanning tree are cut out.
Well, it can be said that this is the core idea of Prim algorithm, but it still needs some skills to implement it.
Because you can't let the computer understand what is "random cutting", you should design mechanized rules and rules to adjust your algorithm and minimize useless work.
Implementation of Prim algorithm
When we think about the algorithm problem, if the general situation of the problem is not easy to solve, we can start with a relatively simple special situation. Prim algorithm uses this idea.
According to the definition of "segmentation", as long as the nodes in the graph are cut into two non overlapping and non empty node sets, it can be regarded as a legal "segmentation". Then if I cut out only one node, is it also a legal "segmentation"?
Yes, this is the simplest "segmentation", and the "crosscutting edge" is also well determined, which is the edge of this node.
Then let's choose a point at random. Suppose we start from point A:
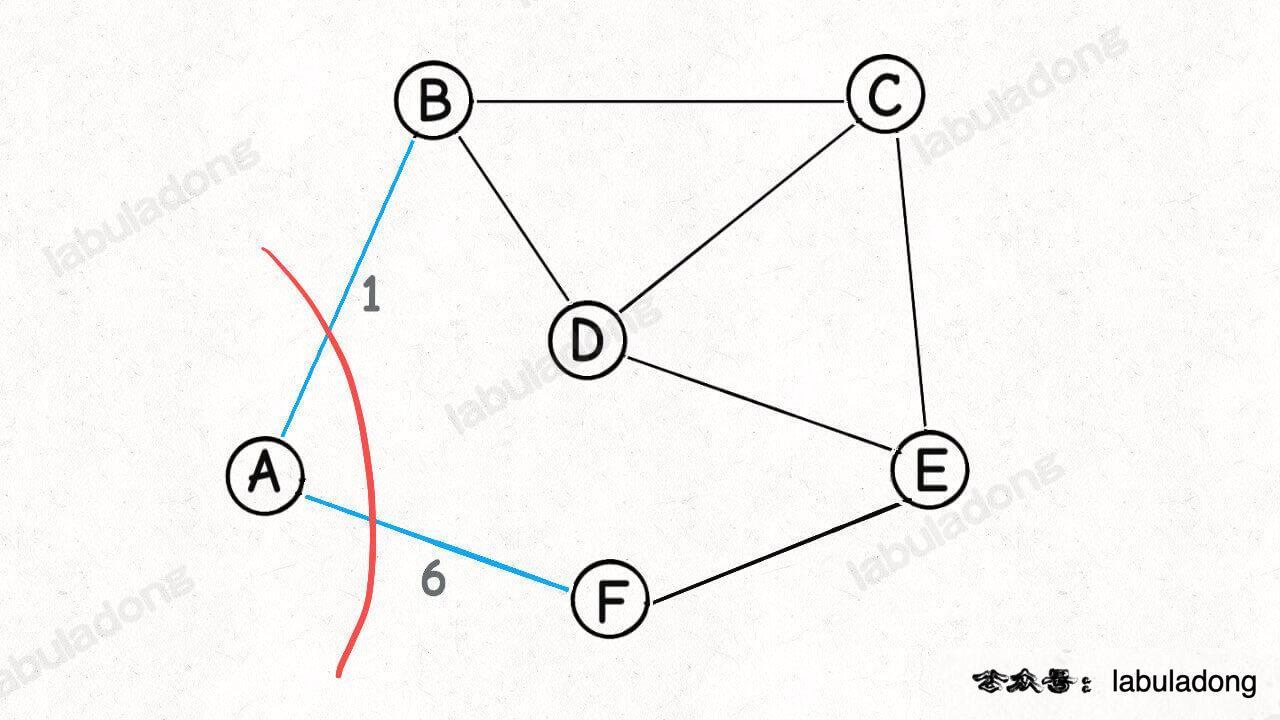
Since this is a legal "segmentation", according to the segmentation theorem, the edge with the smallest weight in AB and AF must be an edge in the minimum spanning tree:
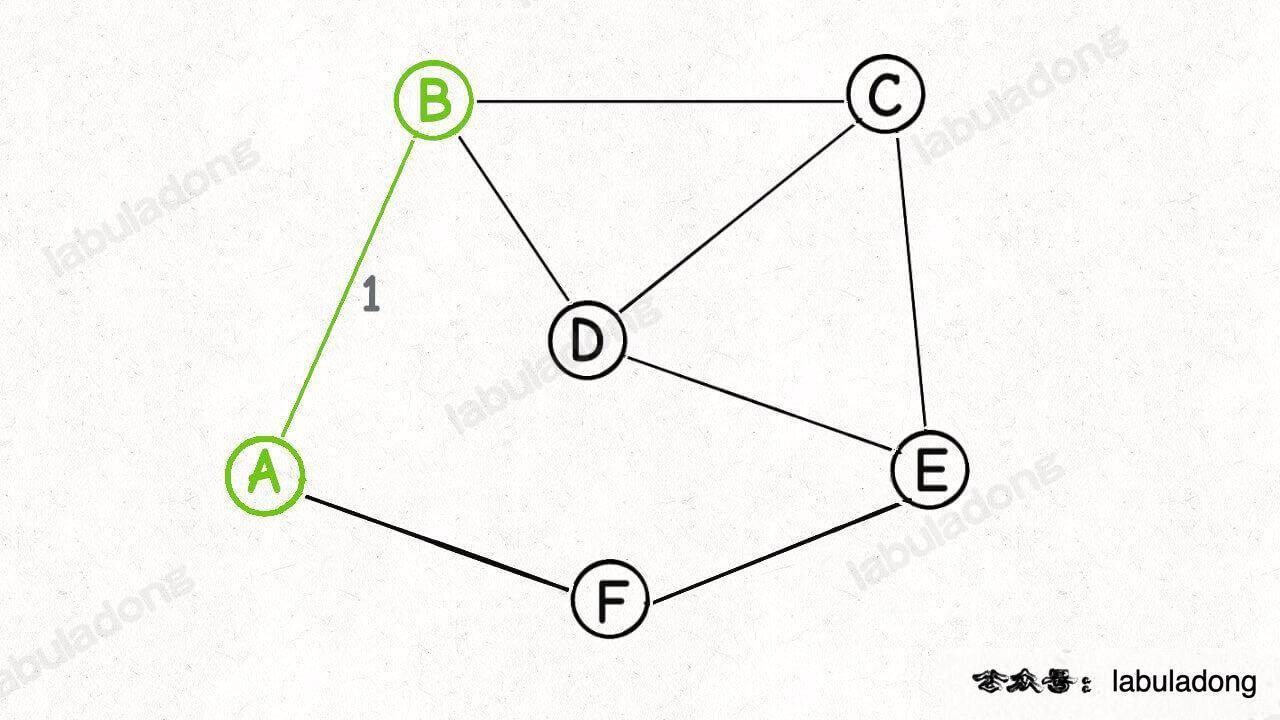
OK, now we have found the first edge (edge AB) of the minimum spanning tree. Then, how to arrange the next "segmentation"?
According to the logic of Prim algorithm, we can cut around two nodes A and B:
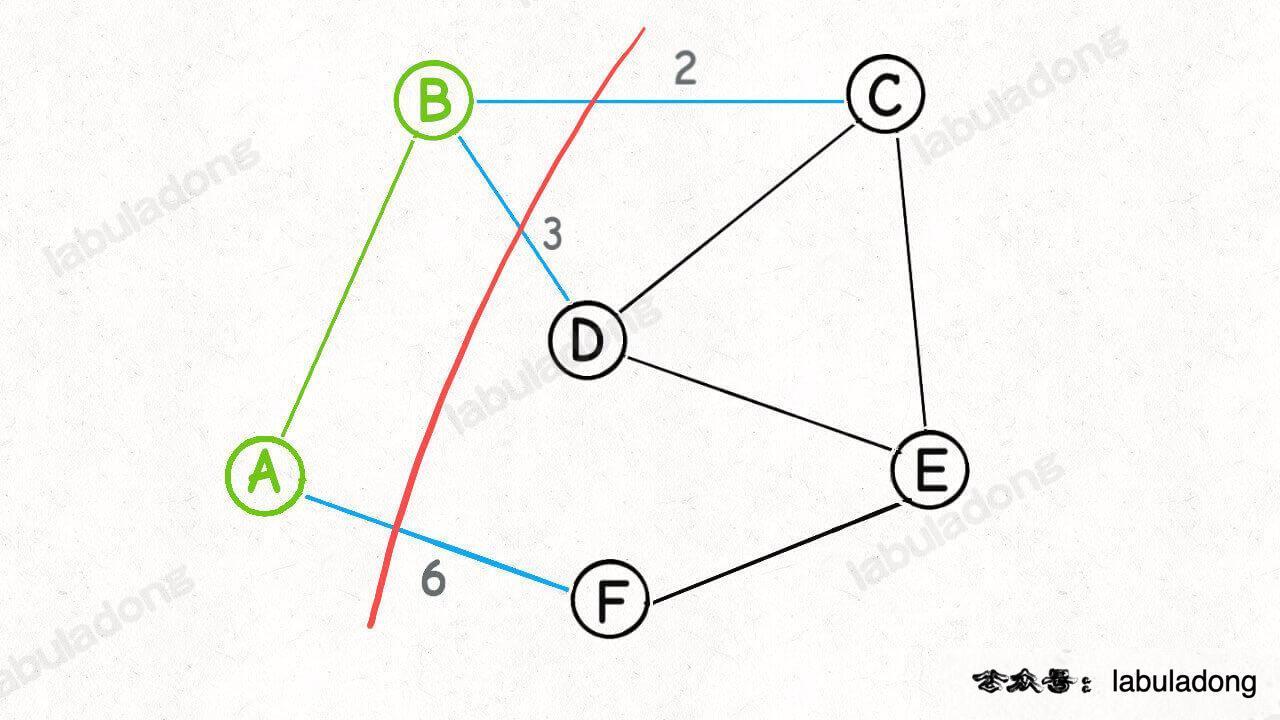
Then, the edge with the smallest weight can be found from the cross cutting edge (blue edge in the figure) generated by this segmentation, that is, the second edge BC in the minimum spanning tree can be found:
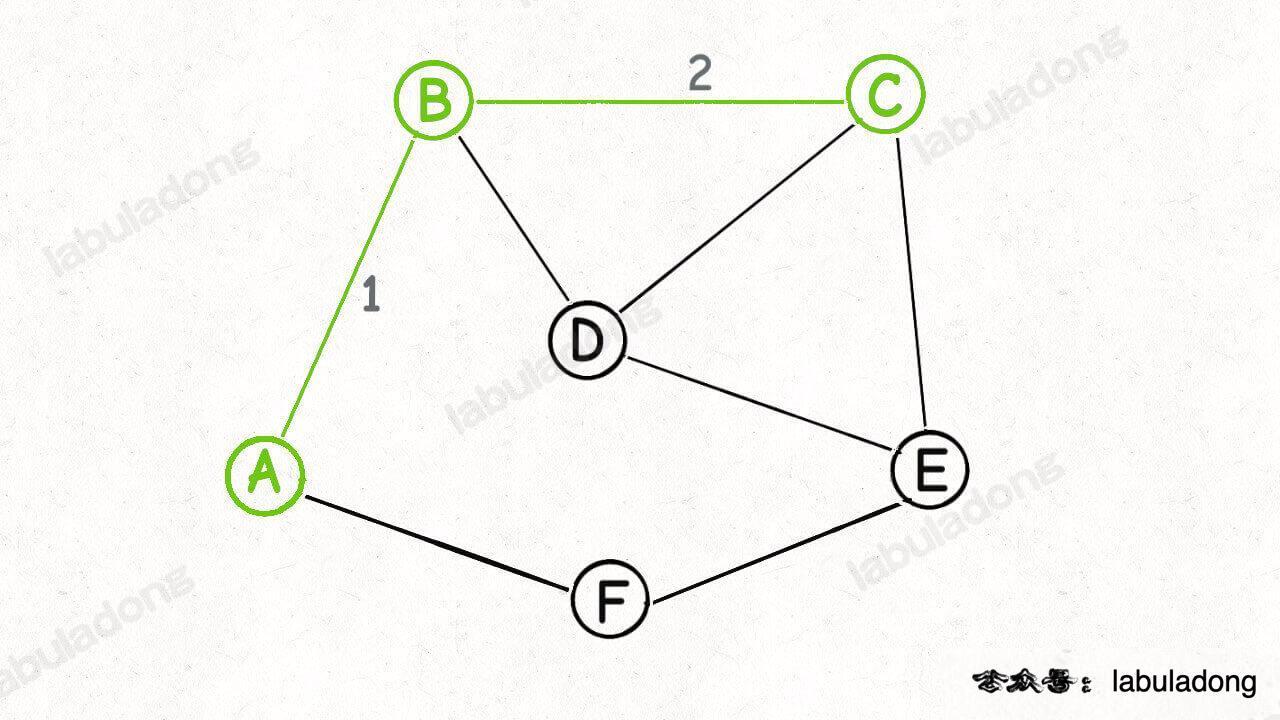
What's next? Similarly, the segmentation is carried out around the three points a, B and C. among the cross cutting edges, the edge with the smallest weight is BD, so BD is the third edge of the minimum spanning tree:
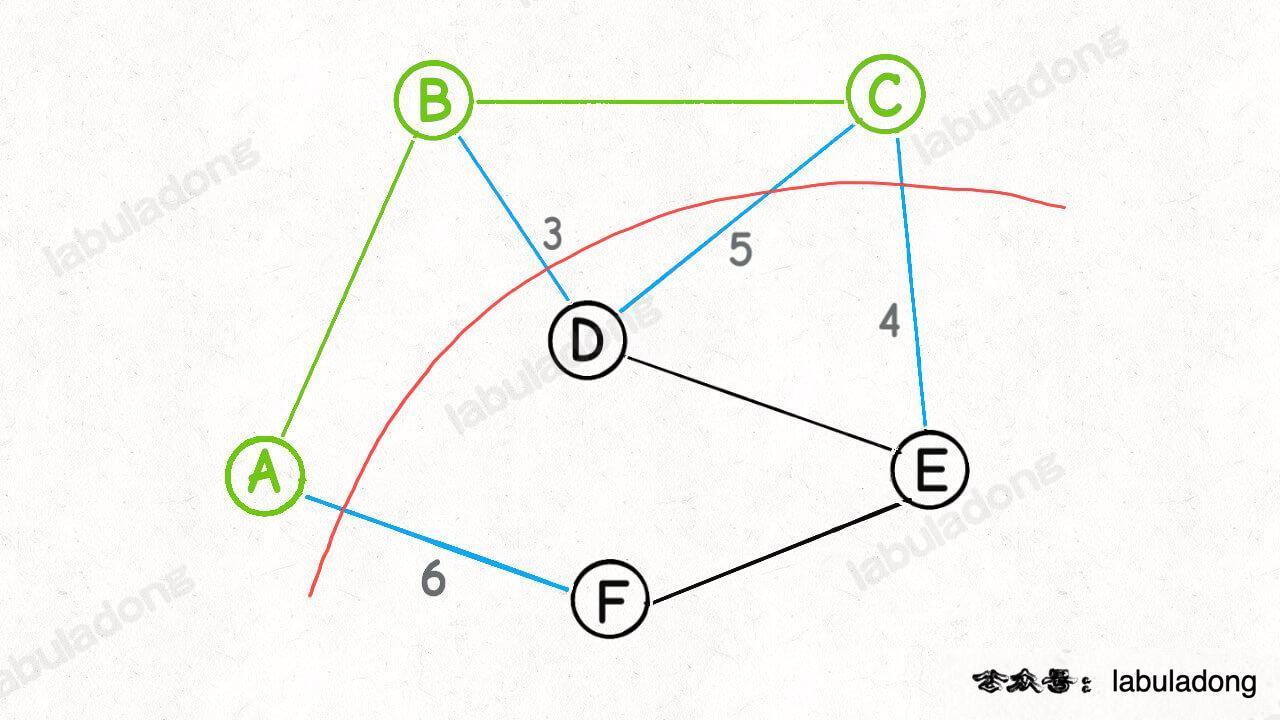
Next, cut around the four points a, B, C and d
The logic of Prim algorithm is like this. Each segmentation can find one edge of the minimum spanning tree, and then a new round of segmentation can be carried out until all edges of the minimum spanning tree are found.
One advantage of this design algorithm is that it is easier to determine the "cross cutting edge" generated by each new "segmentation".
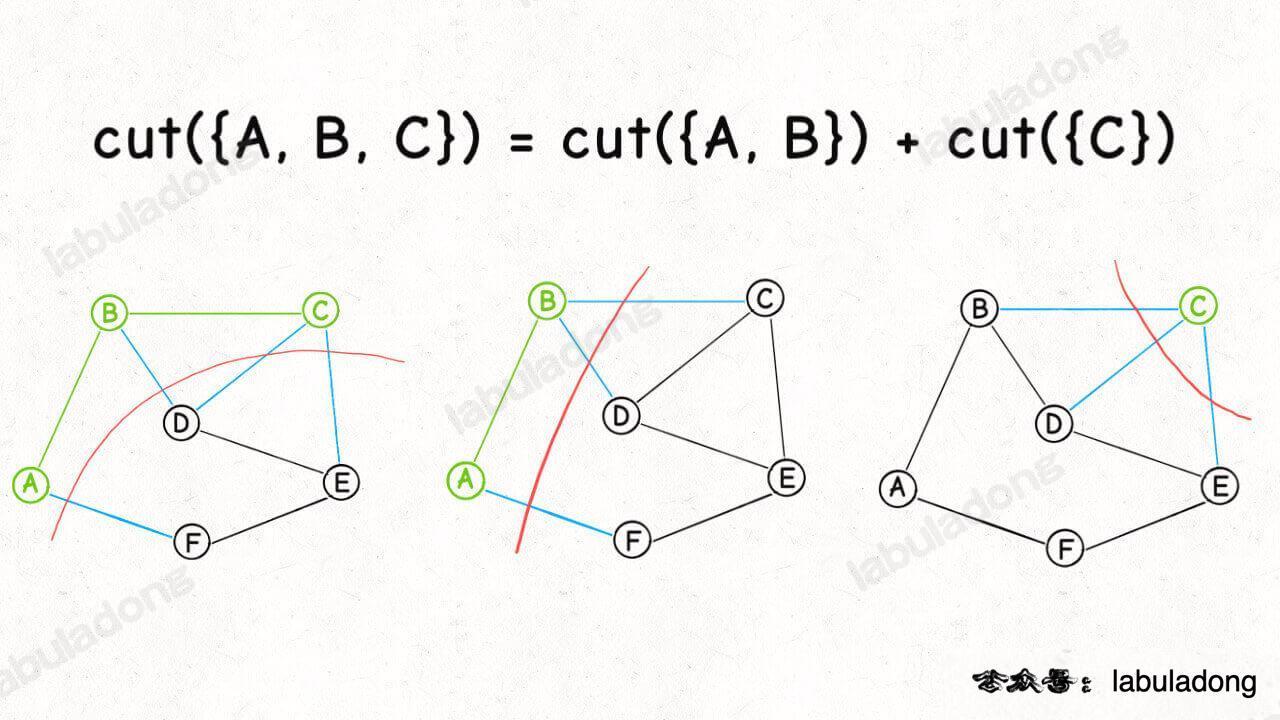
For example, looking back at the graph just now, when I know all the "crosscutting edges" of nodes a and B (which can be expressed as cut({A, B})), that is, the blue edges in the graph:

Can you quickly calculate cut({A, B, C}), that is, what are all the "crosscutting edges" of nodes a, B and C?

Yes, because we found that:
cut({A, B, C}) = cut({A, B}) + cut({C})
And cut({C}) is all adjacent edges of node C:
This feature makes it possible for us to use our code to realize "segmentation" and deal with "crosscutting edges":
In the process of segmentation, we can get all the crosscutting edges of the new segmentation as long as we continuously add the adjacent edges of the new node to the crosscutting edge set.
Of course, careful readers must find that the cross cutting edge of cut({A, B}) and the BC edge of cut({C}) are repeated.
But it's easy to handle. It's OK to use a Boolean array inMST to prevent double calculation of cross cutting edges.
Finally, the purpose of seeking the crosscutting edge is to find the crosscutting edge with the smallest weight. How to do it?
Very simple, using a priority queue to store these crosscutting edges, you can dynamically calculate the crosscutting edge with the lowest weight.
Having understood the principle of the above algorithm, let's take a look at the code implementation of Prim algorithm:
class Prim {
// The core data structure stores the priority queue of "crosscutting edge"
private PriorityQueue<int[]> pq;
// Similar to the function of visited array, it records which nodes have become part of the minimum spanning tree
private boolean[] inMST;
// Record the weight sum of the minimum spanning tree
private int weightSum = 0;
// Graph is a graph represented by adjacency table,
// graph[s] records all adjacent edges of node s,
// The triplet int[]{from, to, weight} represents an edge
private List<int[]>[] graph;
public Prim(List<int[]>[] graph) {
this.graph = graph;
this.pq = new PriorityQueue<>((a, b) -> {
// Sort by the weight of the edges from small to large
return a[2] - b[2];
});
// There are n nodes in the graph
int n = graph.length;
this.inMST = new boolean[n];
// You can start from any point. We might as well start from node 0
inMST[0] = true;
cut(0);
// Continuously segment and add edges to the minimum spanning tree
while (!pq.isEmpty()) {
int[] edge = pq.poll();
int to = edge[1];
int weight = edge[2];
if (inMST[to]) {
// Node to is already in the minimum spanning tree. Skip
// Otherwise, this edge will produce a ring
continue;
}
// Add edge to minimum spanning tree
weightSum += weight;
inMST[to] = true;
// After the node to is added, a new round of segmentation will be carried out, which will produce more cross cutting edges
cut(to);
}
}
// Add the crosscutting edge of s to the priority queue
private void cut(int s) {
// Ergodic adjacent edges of s
for (int[] edge : graph[s]) {
int to = edge[1];
if (inMST[to]) {
// Adjacent contact to is already in the minimum spanning tree, skip
// Otherwise, this edge will produce a ring
continue;
}
// Join the crosscutting queue
pq.offer(edge);
}
}
// Weight sum of minimum spanning tree
public int weightSum() {
return weightSum;
}
// Judge whether the minimum spanning tree contains all nodes in the graph
public boolean allConnected() {
for (int i = 0; i < inMST.length; i++) {
if (!inMST[i]) {
return false;
}
}
return true;
}
}
Understand the segmentation theorem, coupled with detailed code comments, you should be able to understand the code of Prim algorithm.
Here we can review the Prim algorithm and algorithm mentioned at the beginning of this paper Kruskal algorithm Contact:
Kruskal algorithm sorts all edges at the beginning, and then selects the edges belonging to the minimum spanning tree from the edge with the lowest weight to form the minimum spanning tree.
Prim algorithm starts from the segmentation of a starting point (a group of cross cutting edges) to execute the logic similar to BFS algorithm. With the help of segmentation theorem and the dynamic sorting characteristics of priority queue, a minimum spanning tree is "grown" from this starting point.
At this point, what is the time complexity of Prim algorithm?
This is not difficult to analyze. The complexity is mainly in the operation of the priority queue pq. Since pq contains the "edges" in the graph, assuming that the number of edges in a graph is e, the maximum operation is O(E) times pq. The time complexity of each operation priority queue depends on the number of elements in the queue. The worst case is O(logE).
Therefore, the total time complexity of this Prim algorithm is O(ElogE). Think back Kruskal algorithm , its time complexity is mainly to sort all edges by weight, which is also O(ElogE).
But then again, as before Dijkstra algorithm Similarly, the time complexity of Prim algorithm can be optimized, but the optimization point lies in the implementation of priority queue, which has little to do with the algorithm idea of Prim algorithm itself, so we won't discuss it here. Interested readers can search by themselves.
Next, we practice a wave and solve the force deduction problem previously solved with Kruskal algorithm again with Prim algorithm.
Topic practice
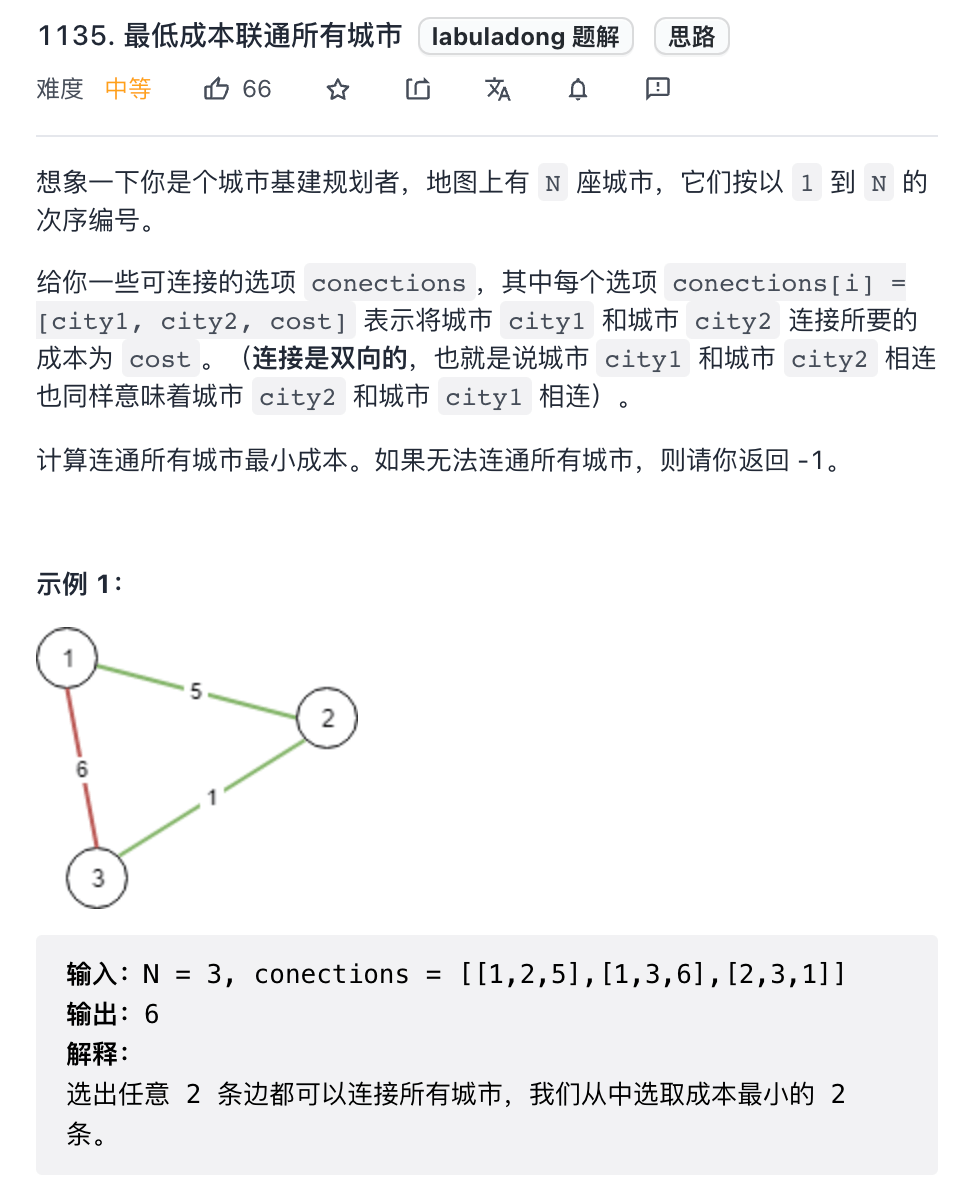
The first question is the deduction of question 1135 "connecting all cities at the lowest cost", which is a standard minimum spanning tree problem:
The function signature is as follows:
int minimumCost(int n, int[][] connections);
Each city is equivalent to the node in the graph, the cost of connecting cities is equivalent to the weight of edges, and the minimum cost of connecting all cities is the sum of the weights of the minimum spanning tree.
Then the solution is obvious. We first convert the connections entered in the topic into the form of adjacency table, and then input it to the Prim algorithm class previously implemented:
public int minimumCost(int n, int[][] connections) {
// Transformed into the form of adjacency table of undirected graph
List<int[]>[] graph = buildGraph(n, connections);
// Execute Prim algorithm
Prim prim = new Prim(graph);
if (!prim.allConnected()) {
// The minimum spanning tree cannot cover all nodes
return -1;
}
return prim.weightSum();
}
List<int[]>[] buildGraph(int n, int[][] connections) {
// There are n nodes in the graph
List<int[]>[] graph = new LinkedList[n];
for (int i = 0; i < n; i++) {
graph[i] = new LinkedList<>();
}
for (int[] conn : connections) {
// The node number given by the title starts from 1,
// But the Prim algorithm we implemented needs to be numbered from 0
int u = conn[0] - 1;
int v = conn[1] - 1;
int weight = conn[2];
// An undirected graph is actually a two-way graph
// An edge is represented as int[]{from, to, weight}
graph[u].add(new int[]{u, v, weight});
graph[v].add(new int[]{v, u, weight});
}
return graph;
}
class Prim { /* See above */ }
There are two points to note about the buildGraph function:
First, the node number given by the topic starts from 1, so let's do the index offset and convert it to start from 0 for the use of Prim class;
The second is how to use adjacency table to represent undirected weighted graph Fundamentals of graph theory algorithm It is said that "undirected graph" can actually be understood as "two-way graph".
In this way, the graph form we transformed corresponds to the previous Prim algorithm class, and the Prim algorithm can be directly used to calculate the minimum spanning tree.
Let's take a look at question 1584 "minimum cost of connecting all points":
For example, the example given in the title:
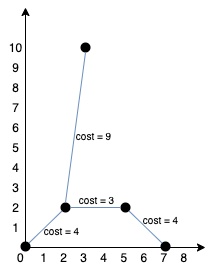
points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
The algorithm should return 20 and connect the points as follows:
The function signature is as follows:
int minCostConnectPoints(int[][] points);
Obviously, this is also a standard minimum spanning tree problem: each point is the node in the undirected weighted graph, the weight of the edge is the Manhattan distance, and the minimum cost of connecting all points is the sum of the weights of the minimum spanning tree.
Therefore, as long as we convert the points array into the form of adjacency table, we can reuse the previously implemented Prim algorithm class:
public int minCostConnectPoints(int[][] points) {
int n = points.length;
List<int[]>[] graph = buildGraph(n, points);
return new Prim(graph).weightSum();
}
// Structural undirected graph
List<int[]>[] buildGraph(int n, int[][] points) {
List<int[]>[] graph = new LinkedList[n];
for (int i = 0; i < n; i++) {
graph[i] = new LinkedList<>();
}
// Generate all edges and weights
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
int xi = points[i][0], yi = points[i][1];
int xj = points[j][0], yj = points[j][1];
int weight = Math.abs(xi - xj) + Math.abs(yi - yj);
// Use the index in points to represent coordinate points
graph[i].add(new int[]{i, j, weight});
graph[j].add(new int[]{j, i, weight});
}
}
return graph;
}
class Prim { /* See above */ }
This problem makes a small modification: each coordinate point is a two tuple, so it is reasonable to use five tuples to represent a weighted edge, but in this case, it is inconvenient to execute Prim algorithm; Therefore, we use the index in the points array to represent each coordinate point, so that we can directly reuse the previous Prim algorithm logic.
Here, the Prim algorithm is finished, and the whole graph theory algorithm is almost the same. Please look forward to more wonderful articles.