brief introduction
As a classical data structure, binary search tree not only has the characteristics of fast insertion and deletion of linked list, but also has the advantage of fast search of array;
Introduction to binary search tree
Binary Search Tree: BST (Binary Search Tree), for any non leaf node of the Binary Search Tree. The value of the left child node is required to be smaller than that of the current node, and the value of the right child node is required to be larger than that of the current node.
Special note: if you have the same value, you can put this node on the left child node or the right child node.
Binary search tree is a data structure that can efficiently perform the following operations
- Insert a value
- Whether the query contains a value
- Delete a value
In the binary search tree:
- If the left subtree of any node is not empty, the value of all nodes on the left subtree is not greater than that of its root node.
- If the right subtree of any node is not empty, the value of all nodes on the right subtree is not less than the value of its root node.
- The left and right subtrees of any node are also binary search trees.
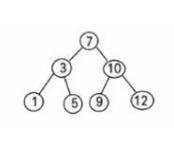
For example, for data (7, 3, 10, 12, 5, 1, 9), the corresponding binary sort tree is
Insert 2 again on the basis:

Middle order traversal of binary tree
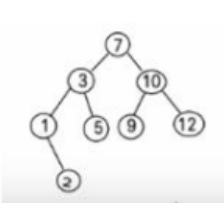
As shown in the figure above, the output after sequence traversal (first output the left child node, then the current node, and finally the right node) is:
1,2,3,5,7,9,10,12
Is an incremental sequence
code:
Method in Node node: (for calling in tree)
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
Middle order traversal in binary search tree:
public void infixOrder(){
if (root!=null){
root.infixOrder();
}else {
System.out.println("The tree is empty and cannot be traversed");
}
}
Insert Knot
Inserting nodes is relatively simple. It mainly compares the nodes to be inserted one by one with the value of the current node. If it is less than the value of the current node. Continue to look to the left, greater than or equal to looking to the right;
code:
add code in Node
//Method of adding nodes
public void add(Node node) {
if (node == null) {
return;
}
if (node.getData() < this.getData()) {
//If it's small, insert it to the left
if (this.left == null) {
this.left = node;
} else {
this.left.add(node);
}
//Greater than or equal to add to the right
} else {
if (this.right == null) {
this.right = node;
} else {
this.right.add(node);
}
}
}
Code of insertion node in BinarySortTree:
public void add(Node node) {
if (root == null) {
root = node;
} else {
root.add(node);
}
}
Delete Vertex
- Leaf node: delete directly without affecting the original tree.
Idea:
1. First find the targetNode of the node to be deleted
2. Find the parent node of targetNode
3. It depends on whether the targetNode is the left child node or the right child node of the parent node
4. Delete according to the corresponding situation
If it is the left child node of parent: parent left = null;
If it is the right child node of parent: parent right = null;
- Nodes with only left or right subtrees: after a node is deleted, move its left or right subtree to the location where the node is deleted, and the child inherits the parent business.
Idea:
1. First find the targetNode of the node to be deleted
2. Find the parent node of targetNode
3. It depends on whether the targetNode is the left child node or the right child node of the parent node
4.1 if it is the left child node of the parent
If target Left = null, then make parent left = target. Right
If target Right = null, then make parent left = target. Left
4.2 if it is the right child node of the parent
If target Left = null, then make parent right = target. Right
If target Right = null, then make parent right = target. Left
- Nodes with both left and right subtrees: find the direct precursor or direct successor s of node p to be deleted, replace node P with s, and then delete node s.
Idea:
Above, we can until the result of middle order traversal is an ascending output. Then can we find a node to replace the node to be deleted? If we find that, we can find the node adjacent to the output sequence root target, that is, the maximum value of the left subtree or the minimum value of the right subtree. Which is it? If you put the same value on the right subtree when you insert the value, you will find the maximum value of the left subtree when you delete it, and vice versa.
1. First find the targetNode of the node to be deleted
2. Find the parent node of targetNode
3. Find the replacement point from the left or right subtree of target
4. Save this node with a temporary variable
5. Then delete this node
6. Make target value = temp. Value is enough
Code implementation:
Find the target Node in Node and find the parent Node
//Find the node to delete
public Node search(int value) {
//If the value to be searched is equal to the value of the current node, it will be returned directly
if (this.getData() == value) {
return this;
}
//If it is not the current value and the value to be searched is less than the value of the current node, search to the left
if (value < this.data) {
//If the left node is not empty, search to the left
if (this.getLeft() != null) {
return this.getLeft().search(value);
} else {//If it is empty, it will directly return null, that is, it is not found
return null;
}
} else {//Find on the right
//The right child node is not empty. Find it on the right
if (this.getRight() != null) {
return this.getRight().search(value);
} else {
return null;
}
}
}
//Get the parent node of the node to be deleted
public Node searchParent(int value) {
//If the root node is to be deleted, the logic can be processed in the tree
//If the child node of the current node is the node to be deleted, return directly
if ((this.left != null && this.left.data == value) || (this.right != null && this.right.data == value)) {
return this;
} else {
//If the search value is less than the value of the current node, search to the left
if (value < this.data && this.left != null) {
return this.left.searchParent(value);
} else if (value >= this.data && this.right != null) {//towards the right
return this.right.searchParent(value);
} else {
return null;
}
}
}
Delete code in BinarySortTree:
public void deleteNode(int value){
//If the number is empty, it ends directly
if (root==null){
return;
}
//First, get the target node
Node target = search(value);
//If not found, end directly
if (target==null){
return;
}
//If the binary tree has only the root node, the node to be deleted is the root node
if (root.getLeft()==null && root.getRight()==null){
root = null;
return;
}
//Get the parent node and start deleting
Node parent = searchParent(value);
if (target.getLeft()==null && target.getRight()==null){//What needs to be deleted is the leaf node
//Judge the parent node of the node to be deleted
if (parent.getLeft()==target){
parent.setLeft(null);
}else {
parent.setRight(null);
}
}else if (target.getLeft()!=null && target.getRight()!=null){//When there are two nodes
int min = GetMaxNode(target.getLeft());
target.setData(min);
}else {//Delete single node
//If the left subtree is deleted
if (target.getLeft()!=null){
if (parent!=null){
if (parent.getLeft()==target){
parent.setLeft(target.getLeft());
}else {
parent.setRight(target.getLeft());
}
}else {
root = target.getLeft();
}
}else {//Delete right subtree
if (parent!=null){
if (parent.getLeft()==target){
parent.setLeft(target.getRight());
}else {
parent.setRight(target.getRight());
}
}else {
root = target.getRight();
}
}
}
}
//Get the minimum value of the current subtree
private int GetMaxNode(Node node){
Node target =node;
while (target.getRight()!=null){
target = target.getRight();
}
deleteNode(target.getData());
return target.getData();
}
//Get the node to be deleted
private Node search(int value){
if (root == null){
return null;
}
return root.search(value);
}
//Get the parent node to be deleted
private Node searchParent(int value){
if (root!=null){
if (value==root.getData()){
return null;
}else {
return root.searchParent(value);
}
}
return null;
}
Full code:
Node:
package binarysorttree;
/**
* @ClassName: Node
* @Author
* @Date 2022/1/25
*/
public class Node {
private int data;
private Node left;
private Node right;
//Construction method
public Node(int data) {
this.data = data;
}
//Method of adding nodes
public void add(Node node) {
if (node == null) {
return;
}
if (node.getData() < this.getData()) {
//If it's small, insert it to the left
if (this.left == null) {
this.left = node;
} else {
this.left.add(node);
}
//Greater than or equal to add to the right
} else {
if (this.right == null) {
this.right = node;
} else {
this.right.add(node);
}
}
}
//Find the node to delete
public Node search(int value) {
//If the value to be searched is equal to the value of the current node, it will be returned directly
if (this.getData() == value) {
return this;
}
//If it is not the current value and the value to be searched is less than the value of the current node, search to the left
if (value < this.data) {
//If the left node is not empty, search to the left
if (this.getLeft() != null) {
return this.getLeft().search(value);
} else {//If it is empty, it will directly return null, that is, it is not found
return null;
}
} else {//Find on the right
//The right child node is not empty. Find it on the right
if (this.getRight() != null) {
return this.getRight().search(value);
} else {
return null;
}
}
}
//Get the parent node of the node to be deleted
public Node searchParent(int value) {
//If the root node is to be deleted, the logic can be processed in the tree
//If the child node of the current node is the node to be deleted, return directly
if ((this.left != null && this.left.data == value) || (this.right != null && this.right.data == value)) {
return this;
} else {
//If the search value is less than the value of the current node, search to the left
if (value < this.data && this.left != null) {
return this.left.searchParent(value);
} else if (value >= this.data && this.right != null) {//towards the right
return this.right.searchParent(value);
} else {
return null;
}
}
}
//Middle order traversal
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
@Override
public String toString() {
return "Node{" +
"data=" + data +
'}';
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
}
BinarySortTree Code:
package binarysorttree;
/**
* @ClassName: BinarySortTree
* @Author
* @Date 2022/1/25
*/
public class BinarySortTree {
Node root = null;
public void add(Node node) {
if (root == null) {
root = node;
} else {
root.add(node);
}
}
public void deleteNode(int value){
//If the number is empty, it ends directly
if (root==null){
return;
}
//First, get the target node
Node target = search(value);
//If not found, end directly
if (target==null){
return;
}
//If the binary tree has only the root node, the node to be deleted is the root node
if (root.getLeft()==null && root.getRight()==null){
root = null;
return;
}
//Get the parent node and start deleting
Node parent = searchParent(value);
if (target.getLeft()==null && target.getRight()==null){//What needs to be deleted is the leaf node
//Judge the parent node of the node to be deleted
if (parent.getLeft()==target){
parent.setLeft(null);
}else {
parent.setRight(null);
}
}else if (target.getLeft()!=null && target.getRight()!=null){//When there are two nodes
int min = GetMaxNode(target.getLeft());
target.setData(min);
}else {//Delete single node
//If the left subtree is deleted
if (target.getLeft()!=null){
if (parent!=null){
if (parent.getLeft()==target){
parent.setLeft(target.getLeft());
}else {
parent.setRight(target.getLeft());
}
}else {
root = target.getLeft();
}
}else {//Delete right subtree
if (parent!=null){
if (parent.getLeft()==target){
parent.setLeft(target.getRight());
}else {
parent.setRight(target.getRight());
}
}else {
root = target.getRight();
}
}
}
}
//Get the minimum value of the current subtree
private int GetMaxNode(Node node){
Node target =node;
while (target.getRight()!=null){
target = target.getRight();
}
deleteNode(target.getData());
return target.getData();
}
//Get the node to be deleted
private Node search(int value){
if (root == null){
return null;
}
return root.search(value);
}
//Get the parent node to be deleted
private Node searchParent(int value){
if (root!=null){
if (value==root.getData()){
return null;
}else {
return root.searchParent(value);
}
}
return null;
}
public void infixOrder(){
if (root!=null){
root.infixOrder();
}else {
System.out.println("The tree is empty and cannot be traversed");
}
}
}
Test code:
package binarysorttree;
/**
* @ClassName: Test
* @Author
* @Date 2022/1/25
*/
public class Test {
public static void main(String[] args) {
BinarySortTree bs = new BinarySortTree();
int[] arr = {7,7,3,10,12,5,1,9};
for (int i : arr){
bs.add(new Node(i));
}
System.out.println("After insertion");
bs.infixOrder();
bs.deleteNode(7);
bs.deleteNode(3);
bs.deleteNode(10);
bs.deleteNode(12);
bs.deleteNode(5);
bs.deleteNode(1);
bs.deleteNode(9);
bs.deleteNode(9);
System.out.println("-----------------");
System.out.println("After deletion");
bs.infixOrder();
}
}
result: