PSI is an index that we need to pay close attention to before and after risk control modeling. This index directly reflects the stability of the model and has direct reference significance for us to evaluate whether the model needs iteration. Today, I will introduce this indicator from the following aspects.

Index

01 PSI concept 02 PSI generation logic 03 business application of PSI Python implementation of 04 PSI

01 PSI concept

The full name of PSI is called "Population Stability Index", which is a group stability index in Chinese translation. From the perspective of risk control application, it is a grouping test and cross time stability index. When we model, the grouping proportion distribution of data (variables or model scores) is our expectation, that is, we hope to show a similar grouping distribution in the test data set and future data sets, which we call stable. There is no specified value range for PSI value. What we need to know is that the smaller the value, the more stable it is. Generally, 0.25 will be taken as the screening threshold in risk control, that is, if PSI > 0.25, we will determine that this variable or model is unstable. Well, how to calculate the specific PSI? No hurry, please go on to the next section.

02 PSI generation logic

According to the Convention, we first put the calculation formula of PSI:

PSI = \sum\limits_{i=i}^n(A_i-E_i)* ln(\frac{A_i}{E_i})

Where, A_i represents the actual proportion of group i (in the total quantity), E_i represents the expected proportion of group i (that is, the proportion of groups during training or online). Let's take the data in the previous article "risk control ml [5] | must the distribution box be monotonous before woe" as an example. See the following table for details:

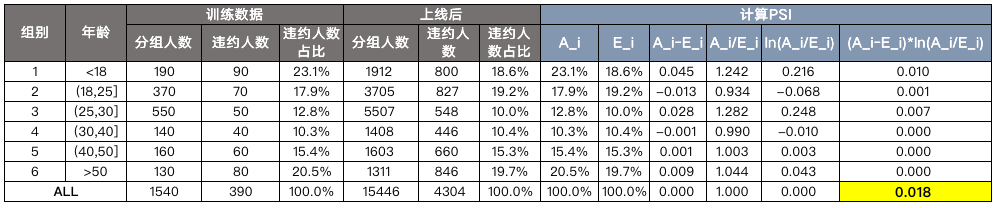
The formula is relatively simple and can be realized in Excel. The calculated PSI is 0.018, so it is stable.

03 business application of PSI

So with this stability index, how can it be applied in specific risk control scenarios? I usually apply it in the following scenarios: 1. Filter variables before modeling 2. Monitor the model after the model goes online

Filter variables before modeling

When making score cards, we usually choose variables with strong stability, because after the model is generally online, the next iteration will be one year later, so we prefer variables with strong stability. How to screen? Let's operate from the following steps: 1) Select the training data and determine the optimal bin of variables (for details, please refer to the previous article on optimal bin)

[1] What are the methods of automatic box division in risk control modeling [2] Code sharing of three continuous variable box dividing methods

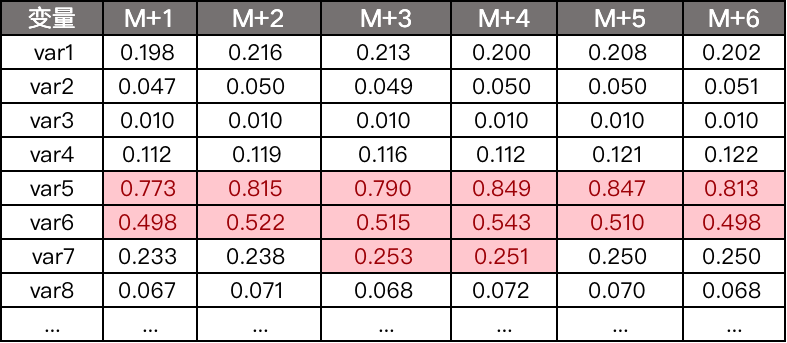
2) Expected proportion distribution of initialization variables 3) Calculate the variable PSI of each month 4) Observe whether there are variables with PSI exceeding 0.25 and eliminate them.

Monitor the model after the model goes online

After the model goes online, we usually group the model points, such as A - F, so we will monitor the grouping stability of the model points. Similarly, the input parameters of the model will also be monitored.

Python implementation of 04 PSI

In the previous article( Code sharing of three continuous variable box dividing methods Based on the automatic box sorting algorithm introduced, the PSI is calculated based on numpy, and the test set can be obtained from the cut keyword input in the background of official account SamShare.

import pandas as pd
import numpy as np
import random
import math
from scipy.stats import chi2
import scipy

# Test data structure, where target is Y, 1 represents bad people and 0 represents good people.  
df = pd.read_csv('./data/autocut_testdata.csv')
print(len(df))
print(df.target.value_counts()/len(df))
print(df.head())

def get_maxks_split_point(data, var, target, min_sample=0.05):
    """ calculation KS value
    Args:
        data: DataFrame，Data set of the optimal cut-off point list of chi square sub box to be calculated
        var: Name of continuous variable to be calculated
        target: Target column to be calculated Y Name of
        min_sample: int，The minimum data sample of the sub box, that is, the amount of data at least reaches, which is generally used at the sub box point at the beginning or end
    Returns:
        ks_v: KS Value, float
        BestSplit_Point: Return the optimal division point of this iteration, float
        BestSplit_Position: Returns the position of the optimal dividing point, with 0 on the leftmost and 1 on the rightmost, float
    """
    if len(data) < min_sample:
        ks_v, BestSplit_Point, BestSplit_Position = 0, -9999, 0.0
    else:
        freq_df = pd.crosstab(index=data[var], columns=data[target])
        freq_array = freq_df.values
        if freq_array.shape[1] == 1: # If a group has only one enumeration value, such as 0 or 1, the array shape will have problems and jump out of this calculation
            # tt = np.zeros(freq_array.shape).T
            # freq_array = np.insert(freq_array, 0, values=tt, axis=1)
            ks_v, BestSplit_Point, BestSplit_Position = 0, -99999, 0.0
        else:
            bincut = freq_df.index.values
            tmp = freq_array.cumsum(axis=0)/(np.ones(freq_array.shape) * freq_array.sum(axis=0).T)
            tmp_abs = abs(tmp.T[0] - tmp.T[1])
            ks_v = tmp_abs.max()
            BestSplit_Point = bincut[tmp_abs.tolist().index(ks_v)]
            BestSplit_Position = tmp_abs.tolist().index(ks_v)/max(len(bincut) - 1, 1)
        
    return ks_v, BestSplit_Point, BestSplit_Position


def get_bestks_bincut(data, var, target, leaf_stop_percent=0.05):
    """ Calculate the optimal dividing point
    Args:
        data: DataFrame，Data set to be operated
        var: String，Name of continuous variable to be divided into boxes
        target: String，Y Column name
        leaf_stop_percent: The proportion of leaf nodes, as the stop condition, is 5 by default%
    
    Returns:
        best_bincut: The best list of syncopation points, List
    """
    min_sample = len(data) * leaf_stop_percent
    best_bincut = []
    
    def cutting_data(data, var, target, min_sample, best_bincut):
        ks, split_point, position = get_maxks_split_point(data, var, target, min_sample)
        
        if split_point != -99999:
            best_bincut.append(split_point)
        
        # The data set is segmented according to the optimal segmentation point, and the segmentation point is calculated recursively for the segmented data set until the stop condition is met
        # print("the value range of this sub box is {0} ~ {1}". Format (data [var]. Min(), data [var] max()))
        left = data[data[var] < split_point]
        right = data[data[var] > split_point]
        
        # When the data set after segmentation is still larger than the minimum data sample requirements, continue segmentation
        if len(left) >= min_sample and position not in [0.0, 1.0]:
            cutting_data(left, var, target, min_sample, best_bincut)
        else:
            pass
        if len(right) >= min_sample and position not in [0.0, 1.0]:
            cutting_data(right, var, target, min_sample, best_bincut)
        else:
            pass
        return best_bincut
    best_bincut = cutting_data(data, var, target, min_sample, best_bincut)
    
    # Fill in the head and tail of the syncopation point
    best_bincut.append(data[var].min())
    best_bincut.append(data[var].max())
    best_bincut_set = set(best_bincut)
    best_bincut = list(best_bincut_set)
    
    best_bincut.remove(data[var].min())
    best_bincut.append(data[var].min()-1)
    # Sort cut point
    best_bincut.sort()
    
    return best_bincut
    

age_bins=get_bestks_bincut(df, 'age', 'target')
df['age_bins'] = pd.cut(df['age'], bins=age_bins)
print("age The optimal dividing point of the box:", age_bins)
print("age The optimal bin division result:\n", df['age_bins'].value_counts())
df.head()

Next, import the test set and calculate the PSI.

# Import test dataset
df_test = pd.read_csv('./data/psi_testdata.csv')

def cal_psi(df_train, df_test, var, target):
    train_bins = get_bestks_bincut(df_train, var, target)
    train_cut_nums = pd.cut(df_train[var], bins=train_bins).value_counts().sort_index().values
    
    # The test set is segmented according to the segmentation point of the training set box
    def cut_test_data(data, var, bincut):
        # Expand the boundary line at both ends
        if bincut[0] > data[var].min()-1:
            bincut.remove(bincut[0])
            bincut.append(data[var].min()-1)
        if bincut[-1] < data[var].max():
            bincut.remove(bincut[-1])
            bincut.append(data[var].max())
    
        # Sort cut point
        bincut.sort()
        return bincut
    
    test_cut_nums = pd.cut(df_test[var], 
                            bins=cut_test_data(df_test, var, train_bins)).value_counts().sort_index().values
    
    tt = pd.DataFrame(np.vstack((train_cut_nums, test_cut_nums)).T, columns=['train', 'test'])
    
    # Calculate PSI
    E = tt['train'].values/tt['train'].values.sum(axis=0)
    A = tt['test'].values/tt['test'].values.sum(axis=0)
    A_sub_E = A-E
    A_divide_E = A/E
    ln_A_divide_E = np.log(A_divide_E) # log in numpy actually refers to ln
    PSI_i = A_sub_E * ln_A_divide_E
    psi = PSI_i.sum()
    return tt, psi
    
tt, psi = cal_psi(df, df_test, 'age', 'target')
print("PSI: ", psi)
tt

Reference

[1] In depth understanding and application of risk control model group stability index (PSI) https://zhuanlan.zhihu.com/p/79682292