catalogue
2, Create a large root heap using an array:
3, What is the time complexity of building a heap?
preface
Previously, we learned about trees and binary trees. We learned that there is a special kind of tree called complete binary tree. If it is a complete binary tree, it can be stored in the array by sequence traversal without causing space loss. Today's heap is also stored in this way. The heap is essentially a complete binary tree, Let's enter the study of heap together!
1, What is a pile?
Firstly, heap is essentially a complete binary tree, which can also be understood as an array physically. Heap can also be divided into two types: large root heap and small root heap, which can also be called maximum heap and minimum heap. The so-called small root pile is that each parent node is smaller than its left and right children, and each tree has such a structure, so it is called a small root pile, and the large root pile is the opposite.
2, Create a large root heap using an array:
To create a large root heap, we must first simulate the given array into a complete binary tree, then adjust its structure and convert it into a large root heap, and then we can carry out a series of operations on this heap.
public class TestHeap {
public int[] elem;
public int usedSize;
public TestHeap() {
this.elem = new int[10];
}
/**
* Implementation of downward adjustment function
* @param parent Root node of each tree
* @param len End position of adjustment for each tree 10
*/
public void shiftDown(int parent,int len) {
int child = 2*parent+1;
//At least there are left children, at least one child
while (child < len) {
if(child+1 < len && elem[child] < elem[child+1]) {
child++;//Ensure the subscript of the maximum value of the current left and right children
}
if(elem[parent] < elem[child]){
int tmp = elem[parent];
elem[parent] = elem[child];
elem[child] = tmp;
parent = child;
child = 2*parent+1;
}else{
break;
}
}
}
//Create a large root heap
public void createHeap(int[] array) {
for (int i = 0; i < array.length; i++) {
elem[i] = array[i];
usedSize++;
}
for (int parent = (usedSize-1-1)/2; parent >= 0 ; parent--) {
//adjustment
shiftDown(parent,usedSize);
}
}
private void shiftUp(int child) {
int parent = (child - 1) / 2;
while(child > 0){
if(elem[parent] > elem[child]){
break;
}else{
int tmp = elem[parent];
elem[parent] = elem[child];
elem[child] = tmp;
child = parent;
parent = (child - 1) / 2;
}
}
}
//Put element
public void offer(int val) {
if(isFull()) {
//Capacity expansion
elem = Arrays.copyOf(elem,2*elem.length);
}
elem[usedSize++] = val;
//Note that usedSize-1 is passed in here
shiftUp(usedSize-1);
}
public boolean isFull() {
return usedSize == elem.length;
}
//Out of the team
public int poll(){
if(isEmpty()){
throw new RuntimeException("Priority queue is empty!");
}
int tmp = elem[0];
elem[0] = elem[usedSize - 1];
elem[usedSize - 1] = tmp;
usedSize -- ;
shiftDown(0,usedSize);
return tmp;
}
//Priority queue top
public int peek(){
if(isEmpty()){
throw new RuntimeException("Priority queue is empty!");
}
return elem[0];
}
public boolean isEmpty() {
return usedSize == 0;
}
//Heap sort
public void heapSort() {
int end = this.usedSize - 1;
while(end != 0){
int tmp = elem[0];
elem[0] = elem[end];
elem[end] = tmp;
shiftDown(0,end);
end --;
}
}
}3, What is the time complexity of building a heap?
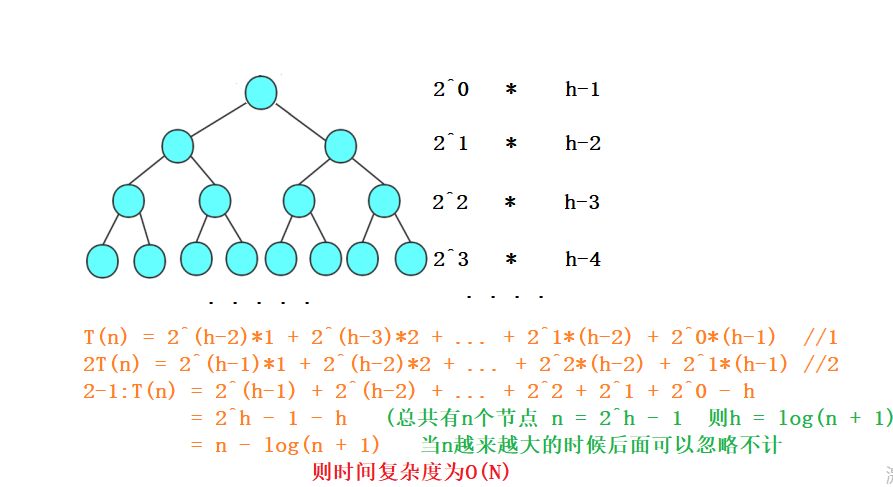
4, PriorityQueue:
When creating a priority queue, its source code is to create a small root heap. Of course, some methods can be used to create a large root heap, such as lambda expression, but it is not readable. You can also create a comparator to create:
//How to create a large root heap
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {
@Override//comparator
public int compare(Integer o1, Integer o2) {
return o1 - o2;
}
});
//lambda expression: but poor readability
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>((x,y)->{return y - x;});
The most classic topk problem:
public static List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
PriorityQueue<List<Integer>> maxHeap = new PriorityQueue<>(k, new Comparator<List<Integer>>() {
@Override
public int compare(List<Integer> o1, List<Integer> o2) {
return (o2.get(0)+o2.get(1))-(o1.get(0)+o1.get(1));
}
});//First create a heap in the form of a large root heap
for(int i = 0;i < Math.min(k, nums1.length); i++){
for (int j = 0; j < Math.min(k, nums2.length); j++) {
//Using the topK method to find the small number of the first k, you need to create a large root heap with the size of K, and then put all the following elements into the heap,
// If it is smaller than the top of the heap, first take the maximum value of the top of the heap out of the queue and then put it into the smaller value. It is possible that this is one of the first k minimum values,
// Finally, the value in the heap is the first k smallest value, and the top of the heap is the K smallest value
//The same is true for the first k maximum values, just create a small root heap
if(maxHeap.size() < k){
List<Integer> ret = new ArrayList<>();
ret.add(nums1[i]);
ret.add(nums2[j]);
maxHeap.offer(ret);
}else{
int top = maxHeap.peek().get(0) + maxHeap.peek().get(1);//Get stack top element
if(top > nums1[i] + nums2[j]){//Compare which one is smaller, and then put it into the heap
maxHeap.poll();
List<Integer> ret = new ArrayList<>();
ret.add(nums1[i]);
ret.add(nums2[j]);
maxHeap.offer(ret);
}
}
}
}
List<List<Integer>> tmp = new ArrayList<>();
for (int i = 0; i < k && !maxHeap.isEmpty(); i++) {
tmp.add(maxHeap.poll());
}
return tmp;
}
//The first k small numbers
public static int[] topK(int[] array,int k){
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>(){
@Override
public int compare(Integer o1,Integer o2){
return o2 - o1;
}
});
for (int i = 0; i < array.length; i++) {
if(priorityQueue.size() < k){
priorityQueue.offer(array[i]);
}else{
int top = priorityQueue.peek();
if(top > array[i]){
priorityQueue.poll();
priorityQueue.offer(array[i]);
}
}
}
int[] tmp = new int[k];
for (int i = 0; i < tmp.length; i++) {
tmp[i] = priorityQueue.poll();
}
return tmp;
}summary
Binary tree is a common question in the interview, and the heap will also be included, especially the topk question, which is also very common. Later, I will rearrange the heap sorting. This is also a very interesting sorting, of course, it is also very important!!!