Introduction
Priority queue is a widely used data structure in practical projects. Whether it is in the process scheduling of the operating system or in related graph algorithms such as Prim algorithm and Dijkstra algorithm, we can see the appearance of priority queue. In this paper, we will analyze the implementation principle of priority queue.
Priority Queue
Take the process scheduling of the operating system as an example. For example, when we use a mobile phone, the phone assigns higher priority to incoming calls than other programs. In this business scenario, we don't require all elements to be in order, because we only need to deal with the element with the highest current key value (the process with the highest priority).In this case, all we need to do is delete the largest element (get the process with the highest priority) and insert a new element (insert a new process), a data structure called a priority queue.
Let's start by defining a priority queue. Below we'll use pq[] to save the related elements. In the constructor, you can specify the initial size of the heap. If you don't specify an initialization size value, the default initialization value is 1.p.s: Below we will implement the resize() method to dynamically resize the array.
public class MaxPQ<Key> implements Iterable<Key> { private Key[] pq; // store items at indices 1 to n private int n; // number of items on priority queue private Comparator<Key> comparator; // optional Comparator /** * Initializes an empty priority queue with the given initial capacity. * * @param initCapacity the initial capacity of this priority queue */ public MaxPQ(int initCapacity) { pq = (Key[]) new Object[initCapacity + 1]; n = 0; } /** * Initializes an empty priority queue. */ public MaxPQ() { this(1); } }
Basic concepts of heaps
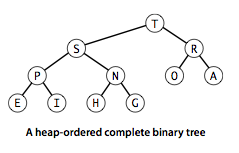
Before formally entering the priority queue analysis, it is necessary to understand the operations related to the heap.We define a binary tree as ordered when each node of the tree is greater than or equal to its two subnodes.The image below is a typical ordered complete binary tree.
Heap float and sink operations
To keep the heap ordered, we need to float and sink the heap. First, we implement two common tool methods, less() for comparing the size of two elements and exch() for exchanging the two elements of an array:
private boolean less(int i, int j) { if (comparator == null) { return ((Comparable<Key>) pq[i]).compareTo(pq[j]) < 0; } else { return comparator.compare(pq[i], pq[j]) < 0; } } private void exch(int i, int j) { Key swap = pq[i]; pq[i] = pq[j]; pq[j] = swap; }
Up Float Operation
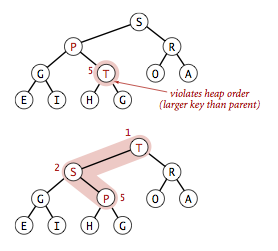
Let's first analyze the floating operation from the following figure. Take swim(5) as an example, and let's look at the floating process.For a heap we float up to keep the heap ordered, that is, a node has a value greater than its child node, so we compare a[5] with its parent node, a[2], and if it is greater than the parent node, we swap the two and continue swim(2).
The specific implementation code is as follows:
private void swim(int k) { while (k > 1 && less(k/2, k)) { exch(k, k/2); k = k/2; } }
Sinking operation
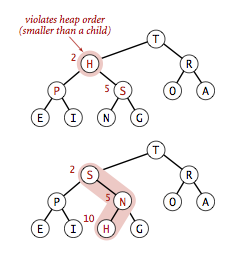
Let's analyze the sink operation from the following figure. Take sink(2) as an example. First, we compare node a[2] with the smaller of its two subnodes. If it is smaller than the subnodes, we exchange the two, and then continue sink(5).
The specific implementation code is as follows:
private void sink(int k) { while (2*k <= n) { int j = 2*k; if (j < n && less(j, j+1)) j++; if (!less(k, j)) break; exch(k, j); k = j; } }
Realization
Let's analyze the process of inserting an element. If we want to insert a new element S into the heap, we first insert this element into the array pq[++n] (the array counts from 1).When we insert S, we break the order of the heap, so we use the float up operation to maintain the order of the heap. When the float up operation is over, we can still ensure that the element of the root node is the largest element in the array.
Next, let's look at the process of deleting the largest element. First we exchange the largest element a[1] with a[n], then we delete the largest element a[n], at which point the heap order has been broken, so we continue to maintain the heap order by sinking, keeping the root node element all elementsThe largest element in the.
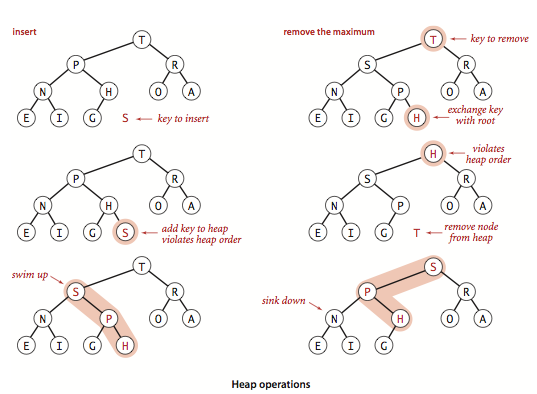
The implementation code inserted is as follows:
/** * Adds a new key to this priority queue. * * @param x the new key to add to this priority queue */ public void insert(Key x) { // double size of array if necessary if (n >= pq.length - 1) resize(2 * pq.length); // add x, and percolate it up to maintain heap invariant pq[++n] = x; swim(n); assert isMaxHeap(); }
The implementation code deleted is as follows:
/** * Removes a maximum key and returns its associated index. * * @return an index associated with a maximum key * @throws NoSuchElementException if this priority queue is empty */ public Key delMax() { if (isEmpty()) throw new NoSuchElementException("Priority queue underflow"); Key max = pq[1]; exch(1, n); n--; sink(1); pq[n+1] = null; // to avoid loiterig and help with garbage collection if ((n > 0) && (n == (pq.length - 1) / 4)) resize(pq.length / 2); assert isMaxHeap(); return max; }
The resize() function, which is used for the size of dynamic arrays, is used in the insert() process above. The implementation code is as follows:
// helper function to double the size of the heap array private void resize(int capacity) { assert capacity > n; Key[] temp = (Key[]) new Object[capacity]; for (int i = 1; i <= n; i++) { temp[i] = pq[i]; } pq = temp; } public boolean isEmpty() { return n == 0; }
isMaxHeap() is used to determine if the current array satisfies the heap ordering principle, which is useful when debug, with the following implementation code:
// is pq[1..N] a max heap? private boolean isMaxHeap() { return isMaxHeap(1); } // is subtree of pq[1..n] rooted at k a max heap? private boolean isMaxHeap(int k) { if (k > n) return true; int left = 2*k; int right = 2*k + 1; if (left <= n && less(k, left)) return false; if (right <= n && less(k, right)) return false; return isMaxHeap(left) && isMaxHeap(right); }
Now that our priority queue is almost complete, notice that we implemented the Iterable<Key>interface above, so we implemented the iterator() method:
/** * Returns an iterator that iterates over the keys on this priority queue * in descending order. * The iterator doesn't implement remove() since it's optional. * * @return an iterator that iterates over the keys in descending order */ public Iterator<Key> iterator() { return new HeapIterator(); } private class HeapIterator implements Iterator<Key> { // create a new pq private MaxPQ<Key> copy; // add all items to copy of heap // takes linear time since already in heap order so no keys move public HeapIterator() { if (comparator == null) copy = new MaxPQ<Key>(size()); else copy = new MaxPQ<Key>(size(), comparator); for (int i = 1; i <= n; i++) copy.insert(pq[i]); } public boolean hasNext() { return !copy.isEmpty(); } public void remove() { throw new UnsupportedOperationException(); } public Key next() { if (!hasNext()) throw new NoSuchElementException(); return copy.delMax(); } }
Heap Sorting
By slightly improving the priority queue above, we can achieve heap sorting, that is, sorting the elements in pq[].For a specific implementation of heap sorting, here are two steps:
First let's build a heap.
Then sort by sinking.
The implementation code for heap sorting is very short. Let's first look at the specific implementation of the code, and then we'll analyze how it works:
/** * Rearranges the array in ascending order, using the natural order. * @param pq the array to be sorted */ public static void sort(Comparable[] pq) { int n = pq.length; for (int k = n/2; k >= 1; k--) sink(pq, k, n); while (n > 1) { exch(pq, 1, n--); sink(pq, 1, n); } }
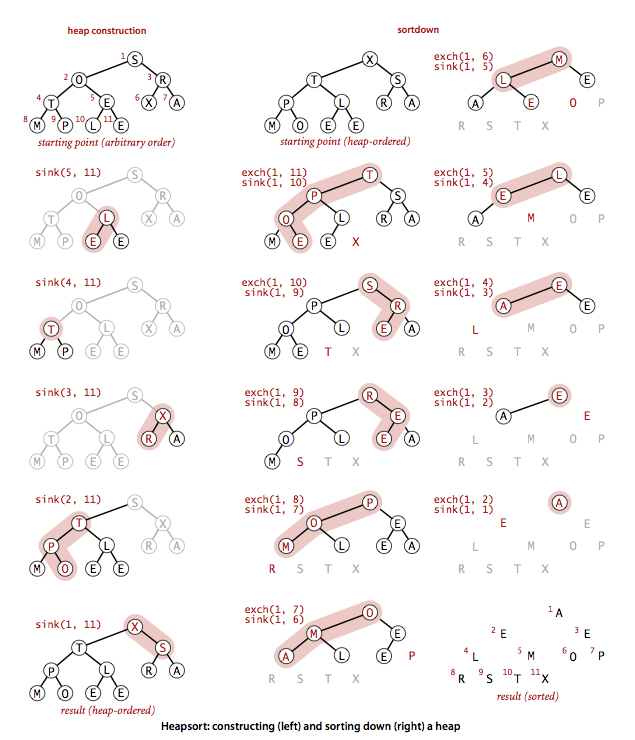
First, let's look at the heap construction process (left in the figure below).We use the sink() method to construct the subheap from right to left.We only need to scan half of the elements in the array, that is, 5, 4, 3, 2, 1.Through these steps, we can get a heap of ordered arrays where each node is larger than its two nodes and the largest element is at the beginning of the array.
Next, let's analyze the implementation of the sink sort (right in the figure below), where we take the approach of deleting the largest element each time, and then reordering the heap with sink(), so that each sink() operation we get to the largest element in the array.