This article talks about the PriorityBlockingQueue, a quote from the book: This is the unbounded blocking queue with priority. Every time you leave the queue, you will return the elements with the highest or lowest priority (here the rules can be made by yourself). The internal is implemented by using the balanced binary tree, and the traversal does not guarantee the order;
In fact, it is also relatively easy to realize a balanced binary tree based on an array. If you don't understand the balanced binary tree, you can first understand it. Don't think about it too hard. The principle is similar to that of a linked list, except that there is only one node pointing to the next node in the linked list, while there are two nodes in the balanced binary tree, one is left, one is right, and the value of the nodes on the left is less than the value of the current node, right The value of edge node is greater than that of current node;
1, Meet PriorityBlockingQueue
The underlying layer is implemented by array. Let's look at several important properties:
//Default initialization capacity of queue private static final int DEFAULT_INITIAL_CAPACITY = 11; //Maximum capacity of array private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8; //Bottom implementation or array private transient Object[] queue; //Queue capacity private transient int size; //A comparator to compare element sizes private transient Comparator<? super E> comparator; //An exclusive lock that controls only one thread in and out of the queue at the same time private final ReentrantLock lock; //If the queue is empty and there are threads coming to the queue to get data, it will block //There is only one condition variable here, because the queue is unbounded. Insert data into the queue CAS Just do it private final Condition notEmpty; //A spin lock, CAS Only one thread can be expanded at the same time. 0 indicates no expansion, 1 indicates expansion in progress private transient volatile int allocationSpinLock;
Just look at the constructor:
//The default array size is 11 public PriorityBlockingQueue() { this(DEFAULT_INITIAL_CAPACITY, null); } //Array size can be specified public PriorityBlockingQueue(int initialCapacity) { this(initialCapacity, null); } //Initializing arrays, locks, conditional variables, and comparators public PriorityBlockingQueue(int initialCapacity, Comparator<? super E> comparator) { if (initialCapacity < 1) throw new IllegalArgumentException(); this.lock = new ReentrantLock(); this.notEmpty = lock.newCondition(); this.comparator = comparator; this.queue = new Object[initialCapacity]; } //This constructor can also pass in a collection public PriorityBlockingQueue(Collection<? extends E> c) { this.lock = new ReentrantLock(); this.notEmpty = lock.newCondition(); boolean heapify = true; // true if not known to be in heap order boolean screen = true; // true if must screen for nulls if (c instanceof SortedSet<?>) { SortedSet<? extends E> ss = (SortedSet<? extends E>) c; this.comparator = (Comparator<? super E>) ss.comparator(); heapify = false; } else if (c instanceof PriorityBlockingQueue<?>) { PriorityBlockingQueue<? extends E> pq = (PriorityBlockingQueue<? extends E>) c; this.comparator = (Comparator<? super E>) pq.comparator(); screen = false; if (pq.getClass() == PriorityBlockingQueue.class) // exact match heapify = false; } Object[] a = c.toArray(); int n = a.length; // If c.toArray incorrectly doesn't return Object[], copy it. if (a.getClass() != Object[].class) a = Arrays.copyOf(a, n, Object[].class); if (screen && (n == 1 || this.comparator != null)) { for (int i = 0; i < n; ++i) if (a[i] == null) throw new NullPointerException(); } this.queue = a; this.size = n; if (heapify) heapify(); }
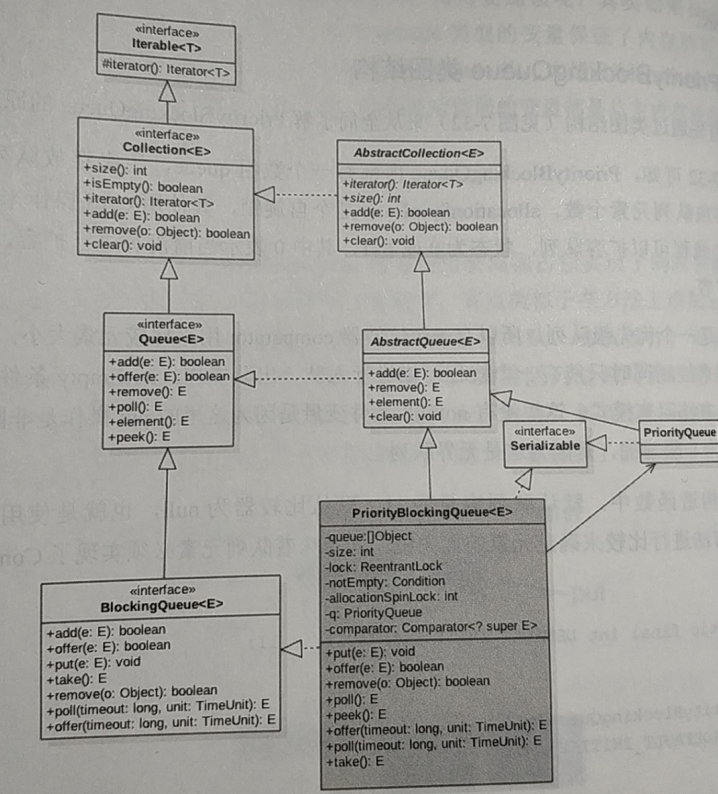
If you are interested in it, please look at the following picture. It's more detailed. I think it's OK to see the important places;
2, offer method
Insert an element into the queue. Since it is an unbounded queue, it always returns true;
public boolean offer(E e) { //If the incoming is null,Throw exception if (e == null) throw new NullPointerException(); final ReentrantLock lock = this.lock; //Get lock lock.lock(); int n, cap; Object[] array; //[1]The total number of actual data in the current array>=Array capacity, expand while ((n = size) >= (cap = (array = queue).length)) //Capacity expansion tryGrow(array, cap); try { Comparator<? super E> cmp = comparator; //[2]When the default comparator is empty if (cmp == null) siftUpComparable(n, e, array); else //[3]If the default comparator is not empty, use the default comparator we passed in siftUpUsingComparator(n, e, array, cmp); //Array actual quantity plus one size = n + 1; //awaken notEmpty Threads in the condition queue notEmpty.signal(); } finally { //Release lock lock.unlock(); } return true; }
In the above code, we can focus on the three areas. First, we need to expand the capacity in [1]:
private void tryGrow(Object[] array, int oldCap) { //First, release the acquired lock. If you don't release it here, it's OK. But sometimes the capacity expansion is slow and takes time. At this time, the entry and exit operations can't be carried out, which greatly reduces the concurrency lock.unlock(); // must release and then re-acquire main lock Object[] newArray = null; //If the spin lock is 0, the queue is not expanded at this time. Then use the CAS Set spin lock from 0 to 1 if (allocationSpinLock == 0 && UNSAFE.compareAndSwapInt(this, allocationSpinLockOffset, 0, 1)) { try { //Using this algorithm to determine the expanded array capacity, we can see that if the current array capacity is less than 64, the new array capacity is 2 n+2,Over 64, new capacity is 3 n/2 int newCap = oldCap + ((oldCap < 64) ? (oldCap + 2) : (oldCap >> 1)); //Judge whether the new array capacity exceeds the maximum capacity. If it exceeds the maximum capacity, try to add one to the old array capacity. If it is still greater than the maximum capacity, throw an exception if (newCap - MAX_ARRAY_SIZE > 0) { // possible overflow int minCap = oldCap + 1; if (minCap < 0 || minCap > MAX_ARRAY_SIZE) throw new OutOfMemoryError(); newCap = MAX_ARRAY_SIZE; } if (newCap > oldCap && queue == array) newArray = new Object[newCap]; } finally { //After the expansion, change the spin lock to 0 allocationSpinLock = 0; } } //The first thread is on the if Execute in CAS After success, the second thread will come here and execute yield Way out CPU,Try to finish the first thread; if (newArray == null) // back off if another thread is allocating Thread.yield(); //The lock is released at the front. We need to acquire the lock here lock.lock(); //Copy elements from the original array to the new array if (newArray != null && queue == array) { queue = newArray; System.arraycopy(array, 0, newArray, 0, oldCap); } }
Look at the default comparator in [2]:
//Here k Represents the actual number in the array, x Represents the data to insert into the array, array Represents an array of data private static <T> void siftUpComparable(int k, T x, Object[] array) { //Therefore, if we want to put the data type in the array, we must implement the Comparable Interface Comparable<? super T> key = (Comparable<? super T>) x; //Here it is used to determine whether there is data in the array. When inserting data for the first time, k=0,If this cycle condition is not met, go to the lowest setting array[0] = key //If this condition is met, first obtain the index of the parent node, then take out the value, and then compare the value with the value to be inserted to decide whether to jump out of the loop or continue the loop //It's more important here. This cycle is to constantly adjust the balance of binary trees. Let's draw a picture while (k > 0) { int parent = (k - 1) >>> 1; Object e = array[parent]; if (key.compareTo((T) e) >= 0) break; array[k] = e; k = parent; } array[k] = key; }
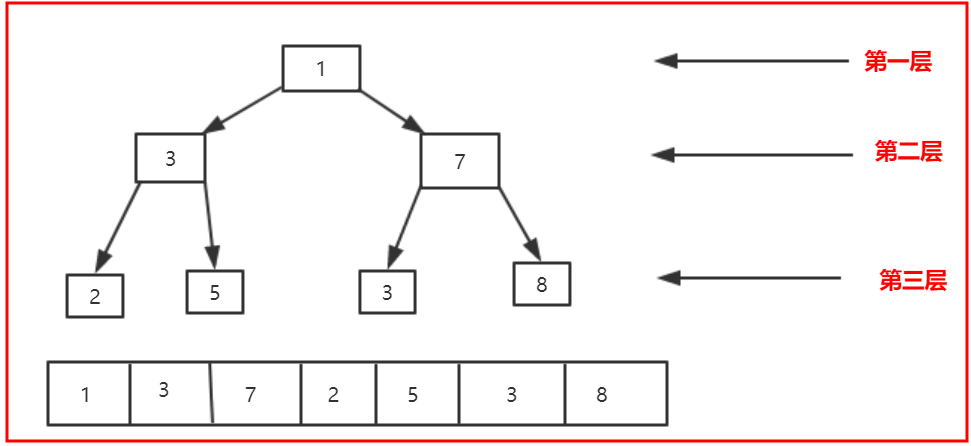
Take a random example to see how to put the elements in the balanced binary tree into the array. The data type in the node is Integer. In fact, each layer is put into the array once from the right. Obviously, it is not in the order of small to large in the array;
Note here that the storage order of balanced binary tree is not unique. There are many situations, which are related to your storage order!
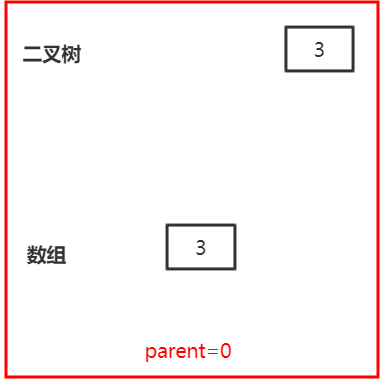
So let's see how the while loop in the siftUpComparable method works? Suppose the first call to offer(3), that is, to call siftupcompatible (0,3, array). Here, assuming that the array has enough size, without considering the expansion, the first call will go to the back of the while loop and execute array[0]=3, as shown in the following figure:
The second call to offer(1), that is, to call siftupcompatible (1,1, array), k=1, parent=0, so the parent node should be 3 at this time, and then 1 < 3, which does not meet the if statement. Set array[1]=3, k=0, and then continue to loop and execute array[0]=1, as shown in the following figure:
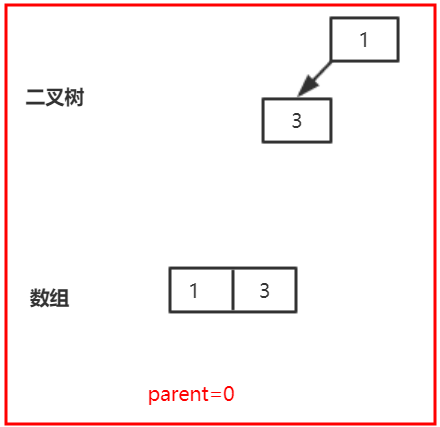
The third call to offer(7), that is, to call siftupcompatible (2,7, array), k=2, parent=0, and the position where the parent node is index 0 is 1. Because 7 > 1 satisfies the if statement, break out of the loop and execute array[2]=7, as shown in the following figure:
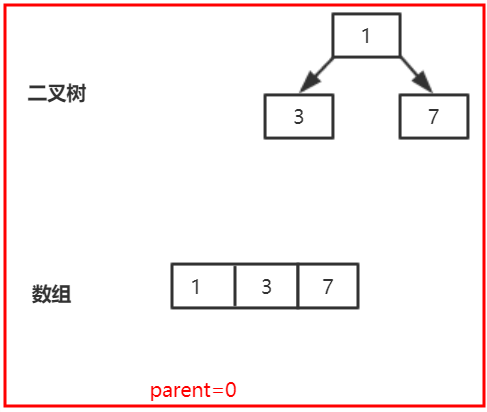
The fourth call to offer(2), that is, to call siftupcompatible (3,2, array), k=3, parent = (k-1) > > 1 = 1, so the parent node represents the position with index 1, that is, 3. Because 2 < 3, does not meet the if statement, set array[3]=3,k=1, and then cycle again, parent=0. At this time, the value of the parent node is 1, 2 < 3, does not meet the if, set array[1]=1,k=0; and then continue the cycle does not meet the cycle Condition, jump out of loop, set array[0] = 2
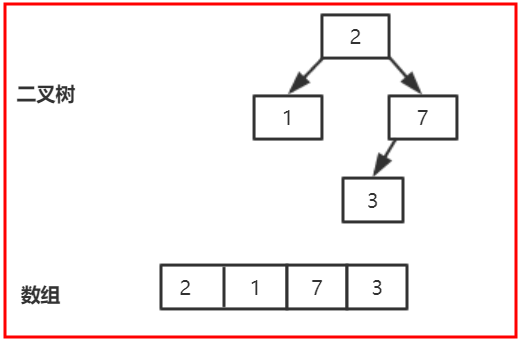
It's still very easy. If you are interested, try adding more nodes! In fact, in [3], we use our custom comparer for comparison. In fact, i is the same as the above code. In addition, the put method is the called offer method, which is not mentioned here
3, poll method
The poll method is used to get and delete the root node of the binary tree inside the queue. If the queue is empty, nul is returned;
public E poll() { final ReentrantLock lock = this.lock; //Obtain the exclusive lock, indicating that no other threads can enter or leave the queue at this time, but the capacity can be expanded lock.lock(); try { //Get and delete the root node as follows return dequeue(); } finally { //Release exclusive lock lock.unlock(); } } //It's interesting to have a good look at this method private E dequeue() { int n = size - 1; //If the queue is empty, return null if (n < 0) return null; else { //Otherwise, get to the array first Object[] array = queue; //Take element 0, which is the root node to return E result = (E) array[0]; //Gets the last element of the actual number of queues and assigns the location to null E x = (E) array[n]; array[n] = null; Comparator<? super E> cmp = comparator; if (cmp == null) //The default comparator is really removing the root node, and then adjusting the entire two balanced tree to achieve a balance. siftDownComparable(0, x, array, n); else //The custom comparer we passed in siftDownUsingComparator(0, x, array, n, cmp); //Then the quantity is reduced by one size = n; //Return to root node return result; } } private static <T> void siftDownComparable(int k, T x, Object[] array, int n) { if (n > 0) { Comparable<? super T> key = (Comparable<? super T>)x; //[1] int half = n >>> 1; // loop while a non-leaf //[2] while (k < half) { int child = (k << 1) + 1; // assume left child is least Object c = array[child]; int right = child + 1; //[3] if (right < n &&((Comparable<? super T>) c).compareTo((T) array[right]) > 0) c = array[child = right]; //[4] if (key.compareTo((T) c) <= 0) break; array[k] = c; k = child; } array[k] = key; } }
So we mainly want to see how to adjust the balance of a balanced binary tree with the root node removed in the siftDownComparable method. For example, there is a balanced binary tree as follows:
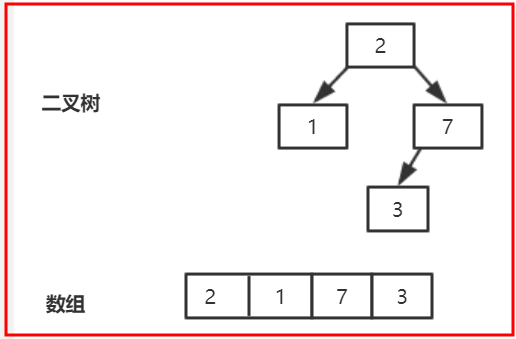
To call the poll method, first save the last element x=3, and then set the last position to null. At this time, the actual call is siftdowncompatible (0,3, array, 3), key=3, half=1, k=0, n=3, which satisfies [2], so child=1, c=1, right=2, which satisfies [3], does not satisfy [4], which sets array[0]=1, k=1; to continue the cycle, which does not satisfy the cycle condition, and to jump out of the cycle , set array[1]=3 directly, and when the poll method returns 2, as shown in the following figure:
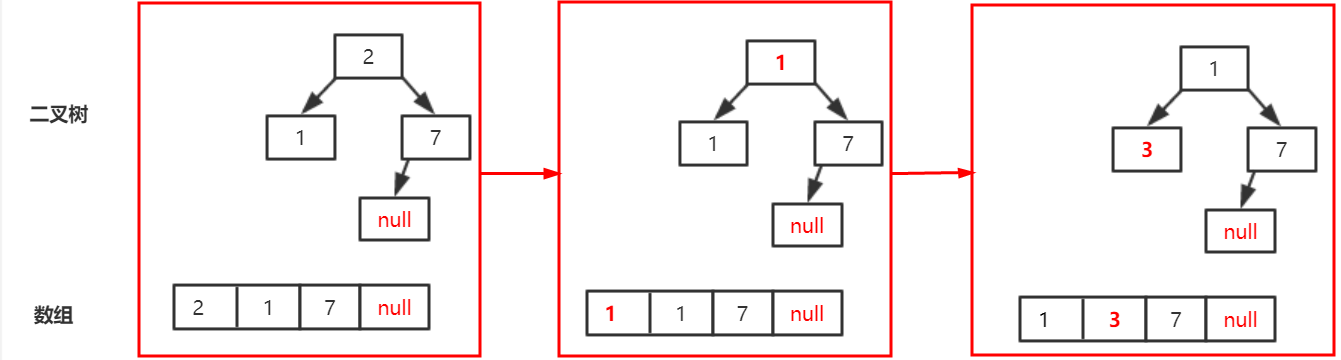
In fact, it can be simply said that the last value x in the array is initially saved and inserted into the binary tree at the right time. When is the right time? First, after removing the root node, get the values of leftVal and rightVal of the left and right child nodes of the root node. If x is smaller than leftVal, put x directly in the position of the root node, and the whole balanced binary tree will be balanced! If x is larger than leftVal, set the value of leftVal to the root node, recurse with the left child node, and continue to compare the size of the left node of X and the left child node! It's OK to have a closer look.
4, take method
The function of this method is to get the root node in the binary tree, that is, the first node of the array. If the queue is empty, it will block;
public E take() throws InterruptedException { //Acquire lock, interruptible final ReentrantLock lock = this.lock; lock.lockInterruptibly(); E result; try { //If the binary tree is empty, then dequeue Method will return null,And then there's a blockage while ( (result = dequeue()) == null) notEmpty.await(); } finally { //Release lock lock.unlock(); } return result; } //As mentioned earlier, the root node is deleted and the balanced two fork tree is adjusted. private E dequeue() { int n = size - 1; if (n < 0) return null; else { Object[] array = queue; E result = (E) array[0]; E x = (E) array[n]; array[n] = null; Comparator<? super E> cmp = comparator; if (cmp == null) siftDownComparable(0, x, array, n); else siftDownUsingComparator(0, x, array, n, cmp); size = n; return result; } }
5, A simple example
I've seen the multiple methods before. Let's talk about how to use them. Let's see how to use the priority blocking queue;
package com.example.demo.study; import java.util.Random; import java.util.concurrent.PriorityBlockingQueue; import lombok.Data; public class Study0208 { @Data static class MyTask implements Comparable<MyTask>{ private int priority=0; private String taskName; @Override public int compareTo(MyTask o) { if (this.priority>o.getPriority()) { return 1; } return -1; } } public static void main(String[] args) { PriorityBlockingQueue<MyTask> queue = new PriorityBlockingQueue<MyTask>(); Random random = new Random(); //Put a task in the queue from TaskName It's put in order. The priority is random for (int i = 1; i < 11; i++) { MyTask task = new MyTask(); task.setPriority(random.nextInt(10)); task.setTaskName("taskName"+i); queue.offer(task); } //Take the task out of the queue. Here it is taken out according to the priority,So I made a sort according to the priority while(!queue.isEmpty()) { MyTask pollTask = queue.poll(); System.out.println(pollTask.toString()); } } }