Before talking about discretization, we can start with simple prefixes and problems to understand the subtlety of discretization
Acwing 795 prefix and

(this question is limited to 2s)
For a small range of prefix sum, you can open an n-size array to store the integer sequence, and then open another n-size array s to store the prefix sum before each subscript. That is, s [i]=s [i-1]+a [i]; Then, when querying the sum in the interval, the direct s [r]- s [l-1] is the interval sum; (here is l-1, because if the subscript is l, s [l] is subtracted; For this problem, the data range of L and r is to [1,1e5]. If the array subscript is directly used to represent L and r, it is also sufficient. However, when the range of L and r is extended to 1e9, the array can not be opened so large. At this time, it can not be represented by array subscript alone.
Such as:
Acwing 802 interval sum

If we use the idea of the previous question to solve this problem, first we need to open an array of 2e9 size. At this time, we need about 4 G of memory space, and the memory is limited. We observe that the total number of points is 1e5, and the initial value of unused points is 0, which has no effect on the prefix and. Therefore, a considerable part of the array with an open 2e9 size is wasted, so we can't allocate every point and every position. Because the points we use are scattered points from point to point, we use the discretization method to map these points to an array, which is the discretization processing method.
Discretization process:
If there are now 1,2,1e7,1e9. The number of four points exists in an array, and each point corresponds to its own value
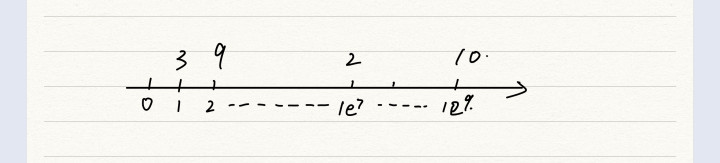
Next, the points are sorted into an array, from large to small. That is, the subscript of the array becomes the subscript of the discrete number, and the discrete number becomes each element of the array

In fact, it is the corresponding method in the figure below.
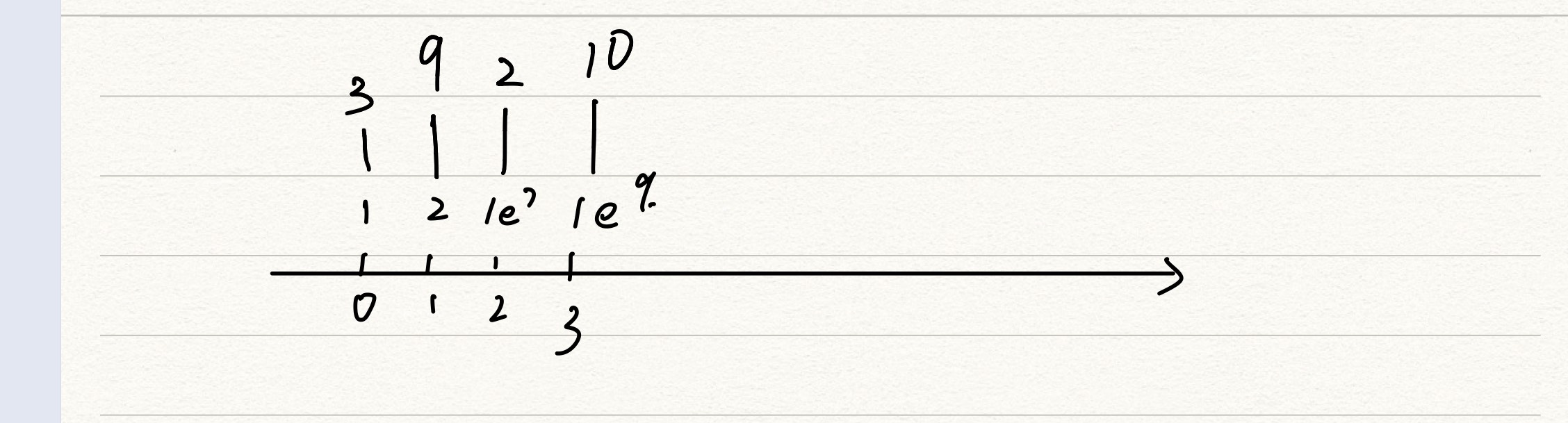
When the elements are repeated, we need to remove the repeated elements.
sort(alls.begin(),alls.end());
alls.erase(unique(alls.begin(),alls.end()),alls.end());
The reason for weight removal is:
When there are two identical elements, the number of their mappings is different. Through binary search, the number of mappings of the previous element is found. At this time, removal can reduce the memory size of the mapping array and improve the efficiency of binary search
Next, when we need to use these points, we can find them from this array.
How to find it? If the traversal from beginning to end is slow, it is still the time complexity of O(n). Here, the binary algorithm is adopted, which can be from O(n) to O(logn);
int find(int x)//Find corresponding subscript { int l=0,r=alls.size(); while(l<r) { int mid=(l+r)/2; if(alls[mid]>x) r=mid; else if(alls[mid]<x) l=mid; else return mid+1; //cout<<l<<r<<endl; } return r+1;//What is returned here is r+1 This is because the array starts from 0, but it is better to start from 1 when calculating the prefix and }
Example:
Acwing 802 interval sum (i.e. the above question)

For this problem, the values of each point are actually scattered. First, we need an array to record all the interval endpoint values, including x, l, r. Can be recorded as array a
For special points, that is, points with their own value value at the endpoint, we need to wrap them with a structure, because a point corresponds to a value, which is put into the corresponding array and recorded as array b.
For the interval value required by the question, we also need an array to store it when outputting the answer. (because I have read the interval endpoint value in array a in the early stage, and I have to output it in the later stage) record it as array c.
The array we want to use to calculate the prefix sum is recorded as prefix array a1. Record the values of each point we need to calculate, record the sum as prefix and array s1, use the value in a1 to convert it into the form of prefix sum, and then output it
At this time, the time complexity is < = O ((n + m) log (n + m))// See whether there is weight removal
#include<iostream> #include<vector> #include<algorithm> using namespace std; const int M=1e6+5; typedef pair<int,int> PI; vector<int>alls;//alls Is the mapping array used for mapping, with find Mapping subscript corresponding to function finding point vector<PI>add,query;//add Is the operand that stores the peer,query Is the storage interval value int a[M],s[M]; int find(int x)//Finding the corresponding subscript is actually the mapping function. What you find is the subscript of large number mapping { int l=0,r=alls.size(); while(l<r) { int mid=(l+r)/2; if(alls[mid]>x) r=mid; else if(alls[mid]<x) l=mid; else return mid+1; //cout<<l<<r<<endl; } return r+1; } int main() { int n,m; cin>>n>>m; for(int i=0;i<n;i++)//Read in the number of point-to-point operations { int x,c; cin>>x>>c; add.push_back({x,c}); alls.push_back(x); } for(int i=0;i<m;i++) { int l,r; cin>>l>>r; query.push_back({l,r}); alls.push_back(l); alls.push_back(r); } //duplicate removal sort(alls.begin(),alls.end()); alls.erase(unique(alls.begin(),alls.end()),alls.end()); for(auto item: add) { int i=find(item.first);//Find the mapping subscript of the number a[i]+=item.second; } for(int i=1;i<=alls.size();i++) s[i]=s[i-1]+a[i];//Calculate prefix and for(auto item: query) { int l=find(item.first),r=find(item.second); cout<<s[r]-s[l-1]<<endl; } return 0; }
This question is a template question, followed by a small variant of the question
Acwing 1952 blonde and N cattle

For this question, to look at it with the idea of violence is to add x, y and z to the three sections. (give the values of a and B, add x to interval [1,A-1], y to interval [A,B], and z to interval [B+1,1e9]). In essence, it is still necessary to operate on an interval. In order to reduce the complexity, the method of difference can be adopted. That is, for each operation
Is a[1]+=x,a[A]-=x,a[A]+=y,a[B+1]-=y,a[B+1]+=z. Finally, calculate the prefix and the maximum value, which is the answer to the question. Because the range of each point is large and the number of points is small, discretization is needed to deal with each endpoint

#include<iostream> #include<algorithm> #include<cstring> #include<vector> using namespace std; const int M=2e6+5; int a[M],s[M]; typedef pair<int,int> PII; vector<int>all;//Array used for mapping vector<PII>add,que; int find(int x)//Mapping function { int l=0,r=all.size(); while(l<r) { int mid=(l+r)/2; if(all[mid]>=x) r=mid; else l=mid+1; } return r+1; } int main() { memset(a,0,sizeof(a)); int n,x,y,z; cin>>n>>x>>y>>z; for(int i=0;i<n;i++) { int l,r; cin>>l>>r; all.push_back(l); all.push_back(r); que.push_back({l,r}); } int ans=0; sort(all.begin(),all.end()); //duplicate removal all.erase(unique(all.begin(),all.end()),all.end()); for(auto item : que) { int l=find(item.first),r=find(item.second); a[1]+=x; a[l]-=x; a[l]+=y; a[r+1]-=y; a[r+1]+=z; //It can also be integrated and written here a[1]+=x;a[l]+=y-x;a[r+1]+=z-y; } for(int i=1;i<=all.size();i++) { a[i]+=a[i-1];//Calculate prefix and ans=max(ans,a[i]); } cout<<ans; }
Acwing 1987 painting fence

For this problem, it can also be transformed into an operation on the interval, that is, when the cow passes through the interval of [L, R], add 1 to [L, R]. When the value in an interval is greater than two, it means that you have walked more than twice
There are some problems that need to be transformed:
For [l, R], when walking to the right, l is the starting point, and R is the step length of L + walking to the left
When left, L is the last position to go right, D - the step length to go right, R is D, the last starting position
If the value in an interval is greater than two, it can be judged by prefix sum. When the prefix sum of a point is greater than two, it means that the cow has passed through this point twice, and the cow must go for the distance from this point to the next point. If the cow walks more than the next point, the initial value of the next point should be 1 when the prefix and calculation are to the next point. Since it is also an interval operation problem, it is best to use the difference algorithm to reduce the time complexity. In this problem, note that the latter point of the difference is a[R] --;
As can be seen from the figure below, the right endpoint is not considered as the road traveled, because the calculation of the next prefix and will be repeated from the right endpoint.
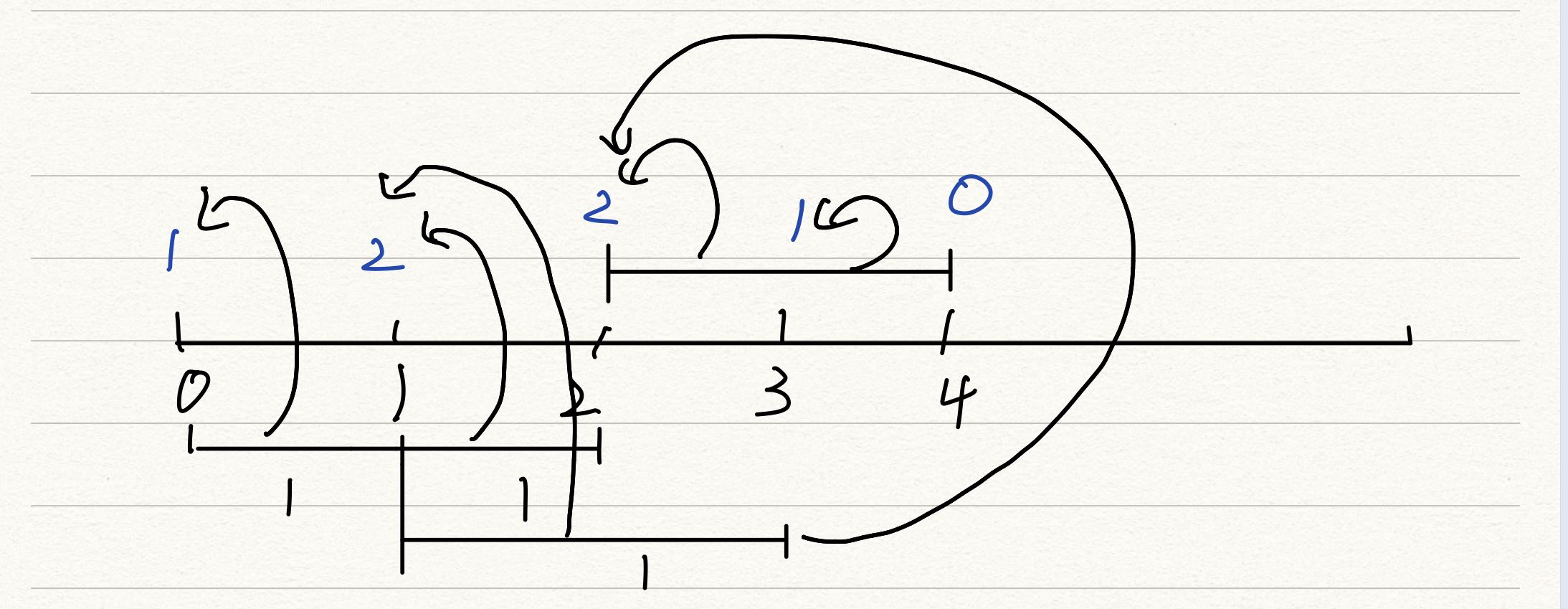
(the arrow indicates which segments the prefix and value of the current point come from)
Because Bessie's walking distance range is [1,2e9], the value is too large. If you want to directly use the subscript to represent the walking coordinates, the memory of the array is too large, and the points are scattered. The default value of each point is 0, which has no impact on the prefix and, so you also need to use dispersion to store each point.
#include<iostream> #include<cstring> #include<algorithm> #include<vector> using namespace std; const int M=1e6+5; typedef pair<int,int>PII; vector<int>all; vector<PII>query; int a[M],s[M]; int find(int x) { int l=0,r=all.size(); while(l<r) { int mid=(l+r)/2; if(all[mid]>=x) r=mid; else l=mid+1; } return r+1; } int main() { memset(s,0,sizeof(s)); int n,sum=0;//See how many paths have been taken in total cin>>n; int l=0; for(int i=0;i<n;i++) { int length,r; char c; cin>>length>>c; if(c=='L') r=l-length; else r=l+length; all.push_back(l); all.push_back(r); if(c=='R') query.push_back({l,r}); else query.push_back({r,l}); //cout<<l<<" "<<r<<endl; l=r;//Is the next point, starting with the destination of the previous point } sort(all.begin(),all.end()); all.erase(unique(all.begin(),all.end()),all.end()); for(auto item: query) { int li=find(item.first),ri=find(item.second);//Found the subscript of the map // cout<<li<<" "<<ri<<endl; //Mark the road section and use the difference a[li]++; a[ri]--;//Not here a[r+1] } for(int i=1;i<=all.size();i++) { s[i]=s[i-1]+a[i];//Calculate the prefix and indicate the total path of the road section //cout<<s[i]<<" "<<a[i]<<endl; if(s[i]>=2) sum+=all[i]-all[i-1];//Notice here, because what's coming back is r+1,all The difference between the subscript and prefix of the array and the subscript that the array wants to express is one } cout<<sum; }
To sum up:
General discretization is to deal with the problem that the number of points is small, but the value of points is large and the array is too large to open. These points can be mapped to an array, and the dichotomy can be used to replace the array to directly access the subscript with a pointer.
The core code is to remove duplication and use dichotomy to find subscripts