
☘ preface ☘
Today is the second day of the nine day training. I will record the learning contents and problem solutions and strive to be the class representative 0.0
be careful!!!! The first solution of problem solution is the solution to be mastered today. The second solution is to study again when you have spare power, involving the following knowledge point 0.0
Link: LeetCode zero basis Guide (Lecture 2) functions
In addition, I won't put the knowledge points I talked about yesterday. If you need to check:
[problem solving report] LeetCode zero foundation guide (Lecture 2) function
🧑🏻 About the author: a young man who changed from industrial design to embedded
✨ Contact: 2201891280(QQ)
⏳ Reading time of the full text: 15min
🎁 Main knowledge points
📝 Use of recycling
In C/C + + language, there are two structures: while and for, but in many cases, there are not many essential differences between them, so we learn for statements that are more convenient for application.
🥨 1. Grammar rules
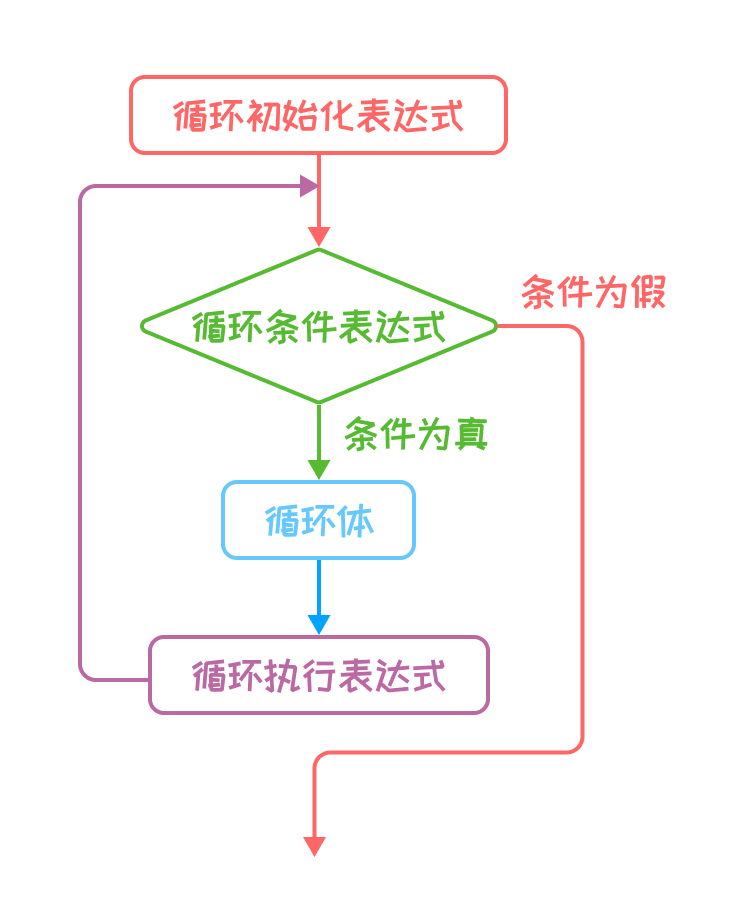
for The expression of the statement is:
for(Loop initialization expression;Cyclic conditional expression;Loop execution expression){
Circulatory body;
}
Its operation process is
- First, execute the loop initialization expression, which will only be executed once!!
- Then, the loop condition expression is executed. If the value is true, the loop body is executed, otherwise it ends.
- Then, the loop execution expression executed after executing the loop body.
- Repeat 2 and 3 until 2 is false and jumps out of the loop.
🥞 2. Simple application
The following program demonstrates a simple solution for the value of 1 + 2 +... + n
int sumNums(int n){ // The parameter passed by the entry function is n
int i; // Declare a variable
int sum = 0; // Initialize to 0 as the returned value
for(i = 1; i <= n; ++i) { // loop
sum += i; // Circulatory body
}
return sum; // Return results
}
🍔 3. Initialization expression
3.1 initialization expression external
Here, the initialization expression is mentioned outside the for loop
int sumNums(int n){ // The parameter passed by the entry function is n
int i = 1; // Declare a variable
int sum = 0; // Initialize to 0 as the returned value
for(; i <= n; ++i) { // loop
sum += i; // Circulatory body
}
return sum; // Return results
}
3.2 initialization expression built in
Here you can directly initialize and assign values. However, the variables will be destroyed directly after using the for loop. So this program is wrong!!!
int sumNums(int n){ // The parameter passed by the entry function is n
for(int i = 1, sum = 0; i <= n; ++i) { // loop
sum += i; // Circulatory body
}
return sum; // Return results
}
3.3 correct usage of initialization expression
In order to use variables later, you need to declare them outside.
int sumNums(int n){ // The parameter passed by the entry function is n
int i,sum;
for(i = 1, sum = 0; i <= n; ++i) { // loop
sum += i; // Circulatory body
}
return sum; // Return results
}
🥙 4. Conditional expression
The conditional expression can be omitted, but it will be an endless loop. The following program must timeout.
int sumNums(int n){ // The parameter passed by the entry function is n
int i = 1; // Declare a variable
int sum = 0; // Initialize to 0 as the returned value
for(;; ++i) { // loop
sum += i; // Circulatory body
}
return sum; // Return results
}
🌮 5. Execute expression
It is a part of the content added after the execution of the structure. It can be placed in the loop itself.
int sumNums(int n){ // The parameter passed by the entry function is n
int i = 1; // Declare a variable
int sum = 0; // Initialize to 0 as the returned value
for(;i<= n; ) { // loop
sum += i; // Circulatory body
i++;
}
return sum; // Return results
}
🍗 After class exercises
Sword finger Offer 64 Find 1 + 2 +... + n
Sword finger Offer 64 Find 1 + 2 +... + n
Title Description
Find 1 + 2 ++ n. It is required that keywords such as multiplication and division, for, while, if, else, switch, case and conditional judgment statements (A?B:C) cannot be used.
Train of thought 1
Pipe so much, cycle punch! No explanation, a little knowledge.
int sumNums(int n){
int i;
int sum = 0;
for(i = 1; i <= n; ++i) {
sum += i;
}
return sum;
}
Train of thought 2
There is no limit to recursion. Recursive rush!
int sumNums(int n){
if(n == 1) return 1;//Recursive exit
return n + sumNums(n - 1); //Next level recursion
}
231. Power of 2
231. Power of 2
Title Description
Give you an integer n, please judge whether the integer is a power of 2. If yes, return true; Otherwise, false is returned.
If there is an integer x such that n == 2x, n is considered to be a power of 2.
Train of thought 1
The same cyclic flushing is good, but pay attention to the overflow problem.
bool isPowerOfTwo(int n){
for(int i = 1;i <= 1<<30;){
if(i == n) return true;
if(i == 1<<30) break; //Prevent overflow
else i*=2;
}
return false;
}
Train of thought 2
In fact, overflow is also a false overflow. It will be easy to turn i into unsigned
bool isPowerOfTwo(int n){
for(unsigned int i = 1;i <= 1<<30;i*=2){
if(i == n) return true;
}
return false;
}
Train of thought 3
Bit operation of advanced usage, bit and
Because the power of 2 has only one 1 in the binary representation, the others are 0, so it's good to judge whether it is 0 with X & (x-1) = = 0
Do not understand, please skip 0.0
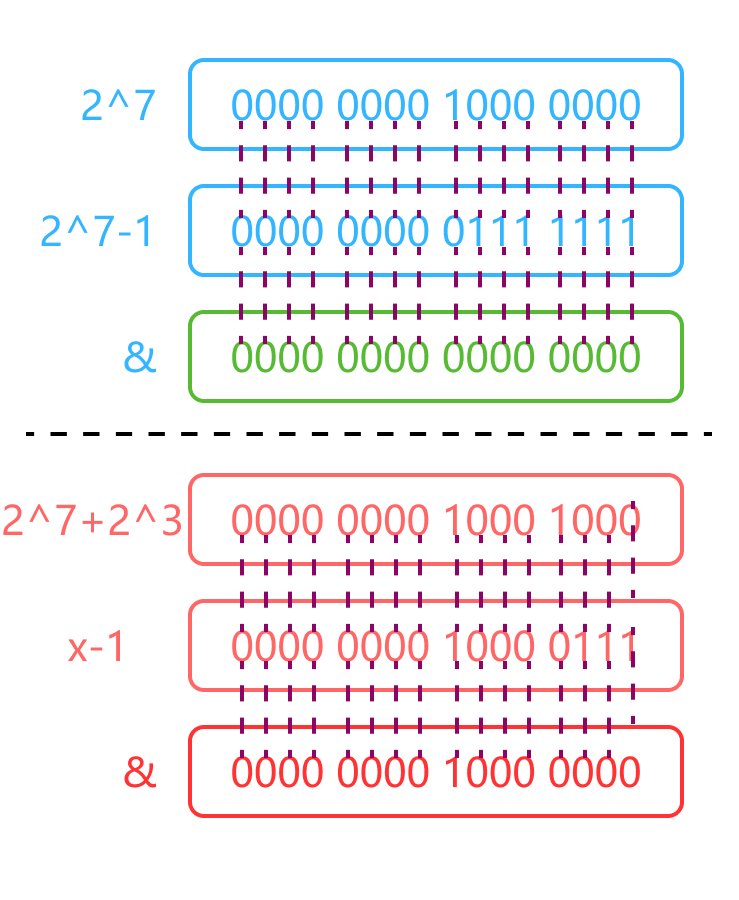
bool isPowerOfTwo(int n){
return n<=0?0:!(n & (n-1));
}
326. Power of 3
326. Power of 3
Title Description
Given an integer, write a function to determine whether it is a power of 3. If yes, return true; Otherwise, false is returned.
The integer n is to the power of 3, which needs to be satisfied: there is an integer x so that n == 3x
thinking
In fact, it's similar to the above. Let's change our thinking this time. The power of 3 must be in addition to 1, and only contains the qualitative factor of 3. We keep dividing 3 to see whether it is 1 in the end.
bool isPowerOfThree(int n){
if(n <= 0) return false;
while(n % 3 == 0) n /= 3;
if(n == 1) return true;
return false;
}
342. Power of 4
342. Power of 4
Title Description
Given an integer, write a function to determine whether it is a power of 3. If yes, return true; Otherwise, false is returned.
The integer n is to the power of 3, which needs to be satisfied: there is an integer x so that n == 3x
thinking
And the power of 3 is the same.
bool isPowerOfFour(int n){
if(n <= 0) return false;
while(n % 4 == 0) //Judge whether it can be divided
n /= 4; //Except 4
return n == 1;
}
1492. Factor k of n
1492. Factor k of n
Title Description
I'll give you two positive integers n and k.
If the positive integer i satisfies n% i = = 0, then we say that the positive integer i is the factor of the integer n.
Consider all factors of integer n and arrange them in ascending order. Please return the k-th factor. If the number of factors of n is less than k, please return - 1.
thinking
Just count whether it reaches the k-th factor directly.
int kthFactor(int n, int k){
for(int i = 1; i <= n ; i++){
if(n % i == 0) k--;
if(!k) return i;
}
return -1; //Finally, k has numbers
}
367. Effective complete square
367. Effective complete square
Title Description
Given a positive integer num, write a function. If num is a complete square number, it returns true, otherwise it returns false.
Advanced: do not use any built-in library functions, such as sqrt.
Train of thought 1
Just go through the search.
int isPerfectSquare(int x){
int i;
long long p;
for(i = 1; ; ++i) {
p = (long long)i*i;
if(p == x) {
return true;
}
if(p > x) {
return false;
}
}
return false;
}
Train of thought 2
To speed up binary search.
bool isPerfectSquare(int num){
unsigned int left = 0, right = 1<<16;//The biggest one is so big
while(left < right){
unsigned int mid = left + (right - left)/2;
if(mid * mid > num) right = mid;
else if(mid *mid == num) return true;
else left = mid + 1;
}
return false;
}
📑 Write at the end
Today, I finished the clock out for the next day. The algorithm notes are very simple. I want to skip the second chapter, but the content is still a little more than 100 million. I'm sure I can finish it more in the evening -- I hope you can come with me. zero