1. Process S (line segment)

1.1 train of thought analysis

The processing of S is relatively simple. We split it horizontally. The original trapezoid remains as an upper trapezoid without degradation:

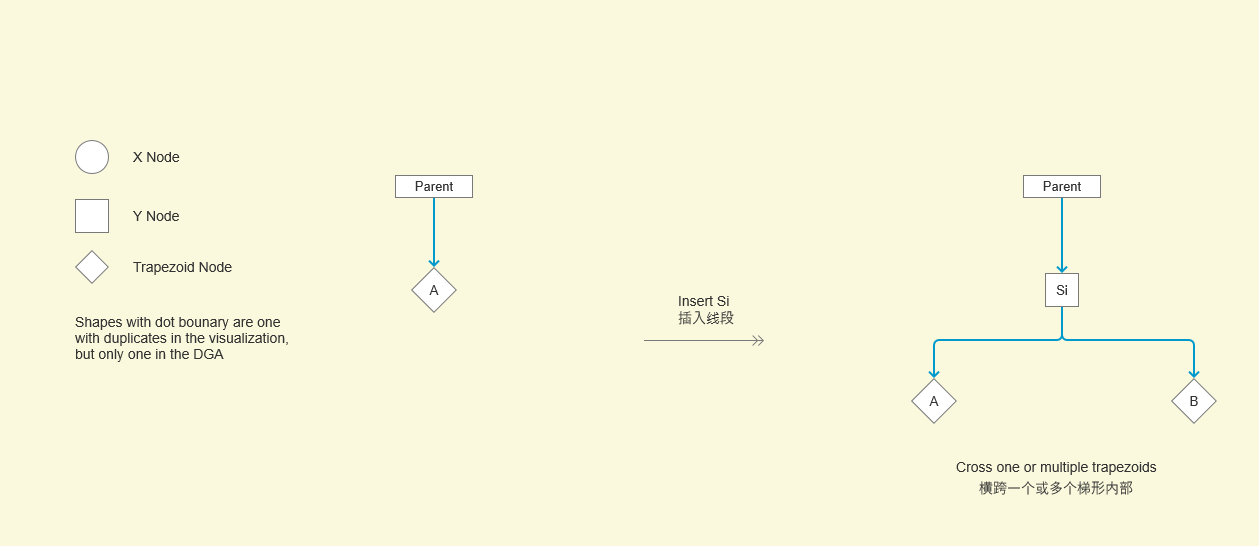
Here, we focus on the merging trapezoid (Trim Wall). The author's splitting idea is as follows:

Merge from left to right; That is, the left side merges the trapezoid on the right;

If the rightP of the current trapezoid is above Si, merge the lower trapezoid; If it is below Si, merge the upper trapezoid; If it is just above Si, do nothing (that is, deal with Qi);

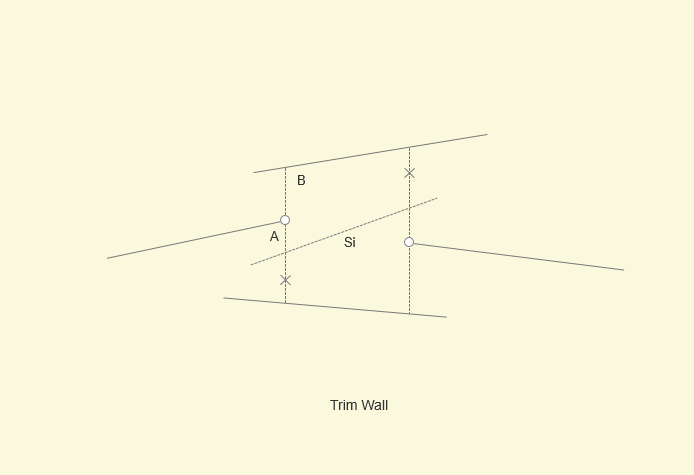
In the example above, if we pass through A trapezoid, its rightP is above Si, so cut the blue dotted line below Si. Similarly, when we pass trapezoid B, its rightP is below Si, so cut the blue dotted line above Si.

1.2 code analysis

1.2. 1 split

In the code analysis part, let'S also take a look at the overall code dealing with S, and then focus on the code logic of splitting and merging:

/**
 * handle S when adding a new segment,
 * this operation will partition the original trapezoid into two parts( horizontal separation ):
 * top(origin)
 * ----------
 *   bottom
 *
 * this method will also handle trimming walls:
 * first, store trapezoids, top and bottom, to be merged later.
 * secondly, merge current top and bottom into previously stored ones.
 * */

// This method is only called when the segment crosses multiple trapezoids
public static
void handleS( SearchVertex d, Line line, Stack<SearchVertex> de ) {
    SearchVertex newer = handleS( d.trapezoid, line, de );
    redirectParents( newer, d );
}

// code to do the separation and update
public static
SearchVertex handleS( Trapezoid middle, Line line, Stack<SearchVertex> de ) {
    Vector p = line.startPoint;
    Vector q = line.endPoint;
    assert Vectors.sortByX( p, q ) <= 0;
    Vector rightP = middle.rightP;

    // horizontal partition
    Trapezoid top = new Trapezoid( p, q, middle.top, line );
    Trapezoid bottom = new Trapezoid( p, q, line, middle.bottom );
    Trapezoid.mergeUppers( top, middle );
    Trapezoid.mergeLowers( bottom, middle );

    // p -> q -> s, no need to trim wall,
    // p -> s, p -> q, s -> s, q -> s need,
    if ( de != null ) {
        // store trapezoids, top and bottom, to be merged later.
        addTrims( top, bottom, rightP, line, de );

        // merge current top and bottom into previously stored ones.
        if ( de.size() > 1 ) {
            SearchVertex trim = trim( de );
            // get trimmed top and bottom
            top = trim.top;
            bottom = trim.bottom;
        }
    }

    // initialize the y node
    SearchVertex YNode = new SearchVertex( line );
    // top trapezoid has been added before?
    if ( top.vertex == null )
        // no, create a new one
        YNode.left = new SearchVertex( top );
    else  {
        // yes, the y node points to it
        assert top.vertex.trapezoid == top;
        YNode.left = top.vertex;
    }
    YNode.left.parents.add( YNode );

    // top trapezoid has been added before?
    if ( bottom.vertex == null )
        // no, create a new one
        YNode.right = new SearchVertex( bottom );
    else {
        // yes, the y node points to it
        assert bottom.vertex.trapezoid == bottom;
        YNode.right = bottom.vertex;
    }
    YNode.right.parents.add( YNode );

    return YNode;
}

First, we split horizontally:

// horizontal partition
Trapezoid top = new Trapezoid( p, q, middle.top, line );
Trapezoid bottom = new Trapezoid( p, q, line, middle.bottom );
Trapezoid.mergeUppers( top, middle );
Trapezoid.mergeLowers( bottom, middle );

Then save the trapezoids to be merged. If there are two trapezoids to be merged, merge them:

// p -> q -> s, no need to trim wall,
// p -> s, p -> q, s -> s, q -> s need,
if ( de != null ) {
    // store trapezoids, top and bottom, to be merged later.
    addTrims( top, bottom, rightP, line, de );

    // merge current top and bottom into previously stored ones.
    if ( de.size() > 1 ) {
        SearchVertex trim = trim( de );
        // get trimmed top and bottom
        top = trim.top;
        bottom = trim.bottom;
    }
}

Finally, the corresponding leaf node is generated, but note that the leaf node here may have been initialized before. Because of the merger relationship, multiple parent nodes will point to the same leaf node:

// initialize the y node
SearchVertex YNode = new SearchVertex( line );
// top trapezoid has been added before?
if ( top.vertex == null )
    // no, create a new one
    YNode.left = new SearchVertex( top );
else  {
    // yes, the y node points to it
    assert top.vertex.trapezoid == top;
    YNode.left = top.vertex;
}
YNode.left.parents.add( YNode );

// bottom trapezoid has been added before?
if ( bottom.vertex == null )
    // no, create a new one
    YNode.right = new SearchVertex( bottom );
else {
    // yes, the y node points to it
    assert bottom.vertex.trapezoid == bottom;
    YNode.right = bottom.vertex;
}
YNode.right.parents.add( YNode );

1.2. 2 consolidation

Finally, let's look at the trim wall code. First, judge whether to merge the upper trapezoid or the lower trapezoid. We use the toLeft test to judge:

/**
 * First process of trimming walls:
 * store trapezoids, top and bottom, to be merged later.
 * */

public static
void addTrims( Trapezoid top, Trapezoid bottom, Vector rightP,
               Line line, Stack<SearchVertex> de  ) {
    SearchVertex trim = new SearchVertex( SearchVertex.NodeType.TRIMMING );

    double res = Triangles.areaTwo( line.startPoint, line.endPoint, rightP );
    // if rightP lies above s, trim lower wall
    if ( MyMath.isPositive( res ) ) {
        bottom.rightP = null;
        top.rightP = rightP;
        trim.isTrimmingTop = false;
    }
    // if rightP lies below s, trim upper wall
    else if ( MyMath.isNegative( res ) ) {
        // assert rightP lies below s
        bottom.rightP = rightP;
        top.rightP = null;
        trim.isTrimmingTop = true;
    }

    // if rightP lies on s, do nothing
    // this happens when handling Q,
    // just trim wall, no need to add ones to be trimmed
    trim.top = top;
    trim.bottom = bottom;
    de.add( trim );
}

We conduct corresponding processing according to the orientation of the current trapezoidal rightP in Si. The code here is basically consistent with our previous explanation. You can understand it in combination with comments. Next is the merged code logic:

/**
 * Second process of trimming walls:
 * secondly, merge current top and bottom into previously stored ones.
 *
 * */

public static
    SearchVertex trim( Stack<SearchVertex> de ) {
    assert de.size() == 2;
    SearchVertex cur = de.pop();
    SearchVertex prev = de.pop();
    assert cur.type == SearchVertex.NodeType.TRIMMING;
    assert prev.type == SearchVertex.NodeType.TRIMMING;

    // trimming top
    if ( prev.isTrimmingTop ) {
        assert check( prev.top, cur.top );
        // merge tops
        Trapezoid.mergeRights( prev.top, cur.top );
        // current top was eaten by previous top
        cur.top = prev.top;
        // link bottoms
        Trapezoid.setUppers( prev.bottom, cur.bottom );
        cur.bottom.leftP = prev.bottom.rightP;
        // at this point, prev.bottom has been all set up
        assert prev.bottom.check();
    }
    // trimming bottom
    else {
        assert check( prev.bottom, cur.bottom );
        // merge bottoms
        Trapezoid.mergeRights( prev.bottom, cur.bottom );
        // current bottom was eaten by previous bottom
        cur.bottom = prev.bottom;
        // link tops
        Trapezoid.setLowers( prev.top, cur.top );
        cur.top.leftP = prev.top.rightP;
        // at this point, prev.top has been all set up
        assert prev.top.check();
    }

    de.push( cur );
    return cur;
}

We combine two upper trapezoids or two lower trapezoids according to the previous judgment. There are two points to note:

1. The left trapezoid annexed the right trapezoid, without exception;
2. Neighbor redirection;

It is recommended that you draw an example to understand the code according to the order of the code. The code is not difficult, but it takes a lot of effort to understand how the merge operation is carried out. In particular, you need to pay attention to the merge and redirection direction. The direction problem is particularly important in computational geometry.

2. Binary search structure

SS basically doesn't have much to discuss, It is basically a binary search tree (but it is not a BST in the strict sense, but a DAG similar to BST), so the update and search operations are very similar to BST, and it should not be too difficult for students familiar with BST to understand. Here we mention the treatment of degradation, that is, PI or Qi already exists in SS. If Pi is located on the vertical line of X-Node, we think Pi is on the right side of X-Node:

case X_POINT_Q, X_POINT_P -> {
    if ( Vectors.isLeft( root.point, p ) )
        return get( root.left, line );

    // whenever p lies on the vertical line of an x-node,
    // we decide that it lies to the right.
    return get( root.right, line );
}

On the other hand, if Pi is above a certain line segment (s, Y-Node), we compare the slopes of S and Si. If the slope of Si is greater, it is considered that Pi is above s, otherwise it is below s:

case SEGMENT -> {
    double res = Triangles.areaTwo( root.line.startPoint, root.line.endPoint, p );

    // whenever p lies on a segment s of a y-node
    // (this can only happen if si shares its left endpoint, p, with s)
    // we compare the slopes of s and si; if the slope of si is larger,
    // we decide that p lies above s, otherwise we decide that it is below s.
    if ( MyMath.isEqualZero( res ) ) {
        if ( Lines.compareBySlope( line, root.line ) > 0 )
            return get( root.left, line );
        else return get( root.right, line );
    }
    else if ( MyMath.isPositive( res ) )
        return get( root.left, line );

    return get( root.right, line );
}

These codes dealing with degradation can be found in the SearchStructure class. Now, we will basically explain how to split and update the ladder diagram and SS. If you have any questions, you can leave a message or contact me~

Previous section: (2) : process P and Q

3. Appendix: Code

3.1 algorithm

Description	Entry method\File
Build trapezoidal map and search structure	SearchStructure trapezoidalMap( List<Line> lines, SearchVertex box )
Point locator	public SearchVertex get( Line line )
Program (including visualization)	Programming Assignment 3 - Trapezoidal Map and Planar Point Location

3.2 data structure

Description	Entry File/Package
Trapezoidal map	public class Trapezoid
Search structure (tree like DAG)	public class SearchStructure

4. References

1. Computational Geometry: Algorithms and Applications
2. Computational geometry ⎯⎯ algorithm and application, translated by Deng Junhui, Tsinghua University Press

5. Disclaimer

※ if there are errors and inaccuracies in this article, you are welcome to correct them~
※ this project is only for learning and communication. Please do not use it for any form of commercial use. Thank you;