catalogue

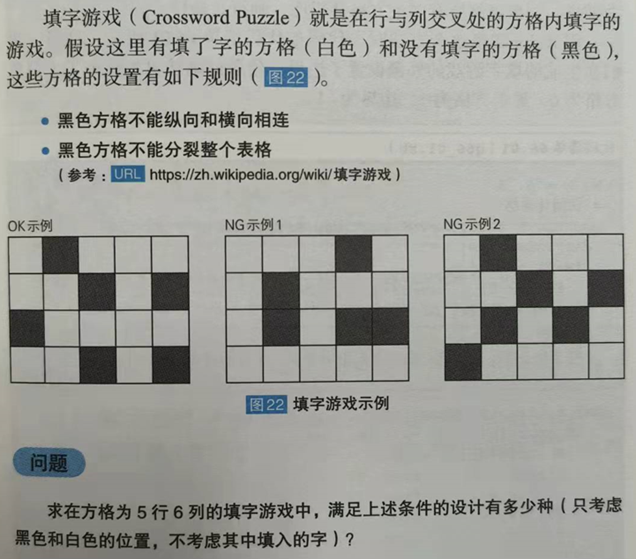
1. Problem description

2. Problem solving analysis

2.1 basic algorithm flow

2.2 connectivity check

3. Code and test

4. Postscript

1. Problem description

 

2. Problem solving analysis

         It is similar to the previous Q32, Q59 and Q68 (I happened to do Q68 first). If you are stuck in thinking about this problem, you can first look at the solutions of the above three questions in this series to see if you can find the clue. If you are still stuck, then look at the solutions of this problem ^ - ^.

2.1 basic algorithm flow

         The basic search framework of this topic is directly based on Q68 (because Q68 was just made a few days ago, it is still fresh in memory and easy to change),

         The algorithm flow is as follows (grids is actually used instead of seats in the code):

 

         Key points:

1. Like Q32, Q59 and Q68, scan line by line and move to the right one grid at a time. The right end moves to the next grid. Reaching the lowest fence line indicates that a search has been completed and a compliant "preliminary" scheme has been found (because the white grid connectivity check has to be done)
2. "Violation inspection" only needs to be carried out for the currently filled black grid. This is because the scanning is carried out in the right and down directions, and only need to check whether there are two adjacent grids that are black

         It differs from Q68 in that:

1. Violation inspection is different
2. The number of black and white squares is not required to be the same, so the search() function does not need to pass in the number of various colors (corresponding to the boy/girl of Q68)

         Finally, the connectivity of the area formed by the white grid is the biggest difference. See the next section for processing methods

 

2.2 connectivity check

         This question requires that after filling in the color, the black grid cannot split the whole table, which is the biggest difference between this question and q32, A59 and q68. In other words, the region composed of white lattice must remain connected, which is equivalent to the reachability problem in graph theory algorithm, that is, starting from a white lattice, if only one lattice is allowed to go horizontally or vertically, it can reach any other white lattice. The classical strategy to solve the reachability problem is depth first search.

         The algorithm flow is as follows:

         Supplementary notes:

1. In this problem, the accessed grid can be cleared directly, so there is no need to set another visited to record the accessed nodes. The advantage of this is that it is also very convenient for the final judgment of whether there are any accessed grids
2. Finally, judge whether there is a grid with 1. Some words mean that there are white grids that are not accessed, that is, the white areas are not connected.

 

3. Code and test

# -*- coding: utf-8 -*-
"""
Created on Wed Oct 20 07:28:54 2021

@author: chenxy
"""

import sys
import time
import datetime
import math
# import random
from   typing import List
from   collections import deque
import itertools as it
import numpy as np

H = 5 # Height, vertical
W = 6 # Width,  horizontal

# grids initialization, with a guard band surrounding the original grids
# The guard band is initialized to '-1' to simplify the judgement processing.
grids = np.zeros((H+2, W+2))
grids[0,:] = -1
grids[H+1,:] = -1
grids[:,0] = -1
grids[:,W+1] = -1

count = 0

def isNG(h,w):
    '''
    '2' represents black.
    Judge whether there are two neighbouring cells are all black

    '''
    return  (grids[h,w]==2) and ((grids[h-1,w]==2) or (grids[h,w-1]==2))

def isAllWhiteConnected(grids)->bool:    
    # Find the first white grid, which is flaged as '1'
    found = False
    for i in range(H):
        for j in range(W):
            if grids[i+1,j+1] == 1:
                start = (i+1,j+1)
                found = True
                break
        if found:
            break
    # print(start)
        
    curGrids = grids.copy()            
    s = deque() # Used as stack, LIFO
    # visited = set() # No need of visited in this problem
    s.append(start)
    # visited.add(start)
    while len(s) > 0:
        cur = s.pop()
        # print(cur)
        curGrids[cur[0],cur[1]] = 0 # Flag it to indicate that it has already been visited.
        if curGrids[cur[0]-1,cur[1]] == 1: # Up grid
            s.append((cur[0]-1,cur[1]))
        if curGrids[cur[0]+1,cur[1]] == 1: # Down grid
            s.append((cur[0]+1,cur[1]))
        if curGrids[cur[0],cur[1]-1] == 1: # Left grid
            s.append((cur[0],cur[1]-1))
        if curGrids[cur[0],cur[1]+1] == 1: # Right grid
            s.append((cur[0],cur[1]+1))        
    return not np.any(curGrids==1)

def arrange_grid(h,w)->int:
    '''
    Parameters
    ----------
    (h,w) : The current exploration point. 
            h represents row index, w represents col index.
    Returns: int
        The number of total arrangement starting from the point (h,w), together 
        with the current grids status, which is a global variable

    '''        
    global count
    # print('h = {0}, w = {1}'.format(h,w))
    if   h == H + 1:
        if isAllWhiteConnected(grids):
            count = count + 1
        # print(grids)    
    elif w == W + 1: # Go to the next row.
        # Reach the right boundary, go to explore the next row from the left 
        arrange_grid(h+1, 1)
    # elif grids[h,w] > 0: 
    #     # This grid has been occupied, move to the right one
    #     arrange_grid(h, w+1)
    else:
        # Try to arrange white to the current grid(h,w). This is always possible
        grids[h,w] = 1
        arrange_grid(h,w+1)            
        grids[h,w] = 0
        # Try to arrange black to the current grid(h,w)
        grids[h,w] = 2
        if not isNG(h,w):
            arrange_grid(h,w+1)            
        grids[h,w] = 0

# # Test of isAllWhiteConnected()
# grids[2,3] = 1
# grids[1,3] = 1
# # print(grids)
# print(isAllWhiteConnected(grids))
                                    
tStart = time.perf_counter()
arrange_grid(1, 1)
tCost  = time.perf_counter() - tStart
print('(H,W)=({0},{1}), count = {2}, tCost = {3:6.3f}(sec)'.format(H,W,count,tCost))  

Operation results:

        (H,W)=(3,4), count = 121, tCost =  0.007(sec)

        (H,W)=(4,5), count = 2749, tCost =  0.244(sec)

        (H,W)=(5,6), count = 149283, tCost = 20.695(sec) 

4. Postscript

        There should be room for optimization in speed, and I will go back to the second round of cleaning up after I have scanned all the problems...

        The advanced chapter is actually done backwards (Q69 -- > q68 -- > Q67 -- > q66...), not intentionally. I usually read the questions first (without looking at the tips and answers in the original book). If I don't have any clue within 5 to 10 minutes, I turn to the next question. If I encounter something similar or have a clue and think it is possible to solve it, I start first, and then it becomes such an order... In front of Q56, the subject of ghost foot picture is completely confused, so we can only store it in our head first

        Previous:

        Next: Q67: is it polite not to sit next to each other?

 

         For the general catalogue of this series, see: Programmer's interesting algorithm: detailed analysis and Python complete solution