Prime number definition

If a number is a prime number, it has only two common factors (divisor) of itself and 1, otherwise it is a composite number.

Write a program to judge whether a number is a prime number

If the data to be judged is N:
The general idea is to divide N from 2 to see whether there is a number that can divide N in the interval [2,N-1]. If so, the surface N is not a prime number, otherwise it indicates that N is a prime number.
The program is implemented as follows:

#include<math.h>
#include<iostream>
using namespace std;
int main()
{
int N,i=2;
cin>>N;
for(i=2;i<N;i++)
{
if(N%i==0)
{
cout<<"false";
break;
}
if(i==N)
cout<<"true";
}
return 0;
}

The above idea is feasible, but if the amount of data is large, it will take a lot of time and can not meet the time requirements, so the composite nature needs to be used.

Composite property

We all know that any positive integer except 1 is either prime or composite. If a number is determined to be prime, it cannot be composite. Similarly, if a number is determined not to be composite, it must be prime. Therefore, we can judge whether a number is a composite number, and then determine whether that number is a prime number.
Composite number property: if a number is a composite number, then the composite number must have a common factor between (1 ~ the square root of the number). If a common factor cannot be found in this interval, then the number must be a prime number. This is an important property of composite numbers. Using this property, we can judge whether it is a prime number by modifying the above procedure.
The certificate is as follows:
There are two facts about composite numbers:

1. Composite number N=m*n;
2. Composite N = (root N) (root N)
   Conclusion:
   If the root sign n is greater than m, then n must be less than the root sign N, similarly
   If the root sign N is less than m, then N must be greater than the root sign N,
   If the root sign n is equal to m, then n must be equal to the root sign N;
   In other words, one of m and N must be less than or equal to the root n.
   Explanation:
   There will be no case where both m and N are greater than root n, because if this happens, mn must be greater than root n, root n, that is, mn > n. This contradicts the facts
   There will be no case where both M and N are less than the root n, because if this happens, m*n must be less than n.

The procedure for judging whether a number is a prime number is changed as follows:

#include<math.h>
#include<iostream>
using namespace std;
int main()
{
int N,i=2,flag=0;
cin>>N;
for(i=2;i<=sqrt(N);i++)
{
if(N%i==0)
{
cout<<"false";
flag=1;
break;
}
}
if(flag==0)
cout<<"true";
return 0;
}

Compared with the above code, this code can reduce sqrt(N)-1 Comparison and greatly reduce the running time when judging whether a number N which is a prime number is a prime number.
We can do a simple test. The comparison times and running time of the two methods are as follows:
Original algorithm:

#include<iostream>
#include<time.h>
using namespace std;
int main()
{
	int N,i,compare = 0;
	clock_t start,end;
	cout<<"please input your number:";
	cin>>N;
	start=clock();
	for(i=2;i<N;i++)
	{
		compare++;
		if(N%i==0)
		{
			cout<<"false"<<endl;
			break;
		}
	}
	if(i==N)
		cout<<"true"<<endl;
	end=clock();
	double seconds  =(double)(end - start)/CLOCKS_PER_SEC;
	cout<<"Total number of comparisons:"<<compare<<"second"<<endl;
	cout << "Running time:" << seconds << "s" << endl;
	return 0;
}

Improved algorithm: (using composite property)

#include<iostream>
#include<math.h>
#include<time.h>
using namespace std;
int main()
{
	int N,i,compare = 0,flag=0;
	clock_t start,end;
	cout<<"please input your number:";
	cin>>N;
	start=clock();
	for(i=2;i<=sqrt(N);i++)
	{
		compare++;
		if(N%i==0)
		{	
			cout<<"false"<<endl;
			flag=1;
			break;
		}
	}
	if(flag==0)
		cout<<"true"<<endl;
	end=clock();
	double seconds  =(double)(end - start)/CLOCKS_PER_SEC;
	cout<<"Total number of comparisons:"<<compare<<"second"<<endl;
	cout << "Running time:" << seconds << "s" << endl;
	return 0;
}

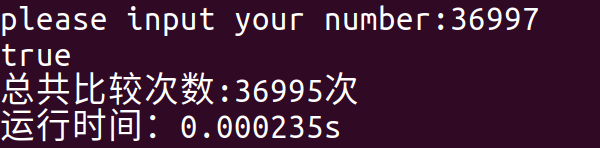
We input the same prime number into the above two programs to test their running time:
Operation results of the original algorithm:

Operation results of improved algorithm:
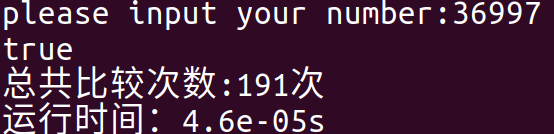Through the comparison of the running results, the running time of the latter is almost 10 times faster than that of the former * * *, which is the charm of the algorithm. At the same time, from the above analysis, we can learn it 10 times faster and beat all the invincible hands in the world