preface

A person can go faster, and a group of people can go further. Exchange and learning plus qq:2096723956
More nanny PX4+ROS learning videos: https://b23.tv/ZeUDKqy
Share knowledge and transfer positive energy. Please point out any omissions or mistakes
Code version: PX4 1.11.3
Code location

1, Position control

void PositionControl::_positionControl()
{

Outer ring position control, only proportional control

Vector3f vel_sp_position = (_pos_sp - _pos).emult(_gain_pos_p);

The expected speed generated by position error and the expected speed are feedforward superimposed. As the total expected speed, it will be superimposed only when the total expected speed and the expected speed generated by position error are not NAN. If the total expected speed is NAN, Then only the expected speed generated by the position error is taken as the total expected speed. If the expected speed generated by the position error is NAN or both the expected speed generated by the position error and the total expected speed are NAN, nothing is done

ControlMath::addIfNotNanVector3f(_vel_sp, vel_sp_position);

If the desired speed generated by the position error is NAN, set it to zero

ControlMath::setZeroIfNanVector3f(vel_sp_position);

The desired speed is limited according to the set horizontal maximum speed and rise / fall maximum speed

	_vel_sp.xy() = ControlMath::constrainXY(vel_sp_position.xy(), (_vel_sp - vel_sp_position).xy(), _lim_vel_horizontal);
	_vel_sp(2) = math::constrain(_vel_sp(2), -_constraints.speed_up, _constraints.speed_down);
}

2, Speed control

void PositionControl::_velocityControl(const float dt)
{

PID control calculates the desired acceleration

Vector3f vel_error = _vel_sp - _vel;
Vector3f acc_sp_velocity = vel_error.emult(_gain_vel_p) + _vel_int - _vel_dot.emult(_gain_vel_d);

The expected acceleration generated by the velocity error and the feedforward superposition of the expected acceleration are taken as the total expected acceleration, and the principle is the same as that of position control

ControlMath::addIfNotNanVector3f(_acc_sp, acc_sp_velocity);

Acceleration control

_accelerationControl();

The speed error limit in the vertical direction is negative because the NED coordinate system is adopted, that is, it is positive when pointing to the ground and the lift is upward. If the lift is greater than-_ lim_thr_min, that is, the absolute value of lift is less than_ lim_thr_min, and the vertical speed error is positive (pointing to the ground), set the vertical speed error to zero, that is, the lift will no longer be reduced. If the lift is less than-_ lim_thr_max, that is, the absolute value of lift is greater than_ lim_thr_max, and the vertical velocity error is negative (pointing to the air), set the vertical velocity error to zero, that is, the lift will no longer increase

if ((_thr_sp(2) >= -_lim_thr_min && vel_error(2) >= 0.0f) ||
    (_thr_sp(2) <= -_lim_thr_max && vel_error(2) <= 0.0f)) {
	vel_error(2) = 0.f;
}

Maximum lift limit

_thr_sp(2) = math::max(_thr_sp(2), -_lim_thr_max);

According to Pythagorean theorem, the square of the maximum thrust in the horizontal direction is equal to the square of the total maximum thrust minus Z Square of thrust in direction．

const float thrust_max_squared = _lim_thr_max * _lim_thr_max;
const float thrust_z_squared = _thr_sp(2) * _thr_sp(2);
const float thrust_max_xy_squared = thrust_max_squared - thrust_z_squared;

Calculate the maximum horizontal thrust by square root

float thrust_max_xy = 0;
if (thrust_max_xy_squared > 0) {
	thrust_max_xy = sqrtf(thrust_max_xy_squared);
}

Horizontal thrust limiting

const Vector2f thrust_sp_xy(_thr_sp);
const float thrust_sp_xy_norm = thrust_sp_xy.norm();
if (thrust_sp_xy_norm > thrust_max_xy) {
	_thr_sp.xy() = thrust_sp_xy / thrust_sp_xy_norm * thrust_max_xy;
}

Anti integral saturation

const Vector2f acc_sp_xy_limited = Vector2f(_thr_sp) * (CONSTANTS_ONE_G / _hover_thrust);
const float arw_gain = 2.f / _gain_vel_p(0);
vel_error.xy() = Vector2f(vel_error) - (arw_gain * (Vector2f(_acc_sp) - acc_sp_xy_limited));

If the integral is NAN, it is set to zero

ControlMath::setZeroIfNanVector3f(vel_error);

Update speed control integral term

_vel_int += vel_error.emult(_gain_vel_i) * dt;

Integral limiting

	_vel_int(2) = math::min(fabsf(_vel_int(2)), CONSTANTS_ONE_G) * sign(_vel_int(2));
}

3, Acceleration control

void PositionControl::_accelerationControl()
{

Assuming that there is only gravitational acceleration in the vertical direction, calculate the unitized resultant force vector, which is the Z-axis vector of the body for attitude generation

Vector3f body_z = Vector3f(-_acc_sp(0), -_acc_sp(1), CONSTANTS_ONE_G).normalized();

Limit the tilt angle, that is, the maximum tilt angle of the generated desired attitude

ControlMath::limitTilt(body_z, Vector3f(0, 0, 1), _constraints.tilt);

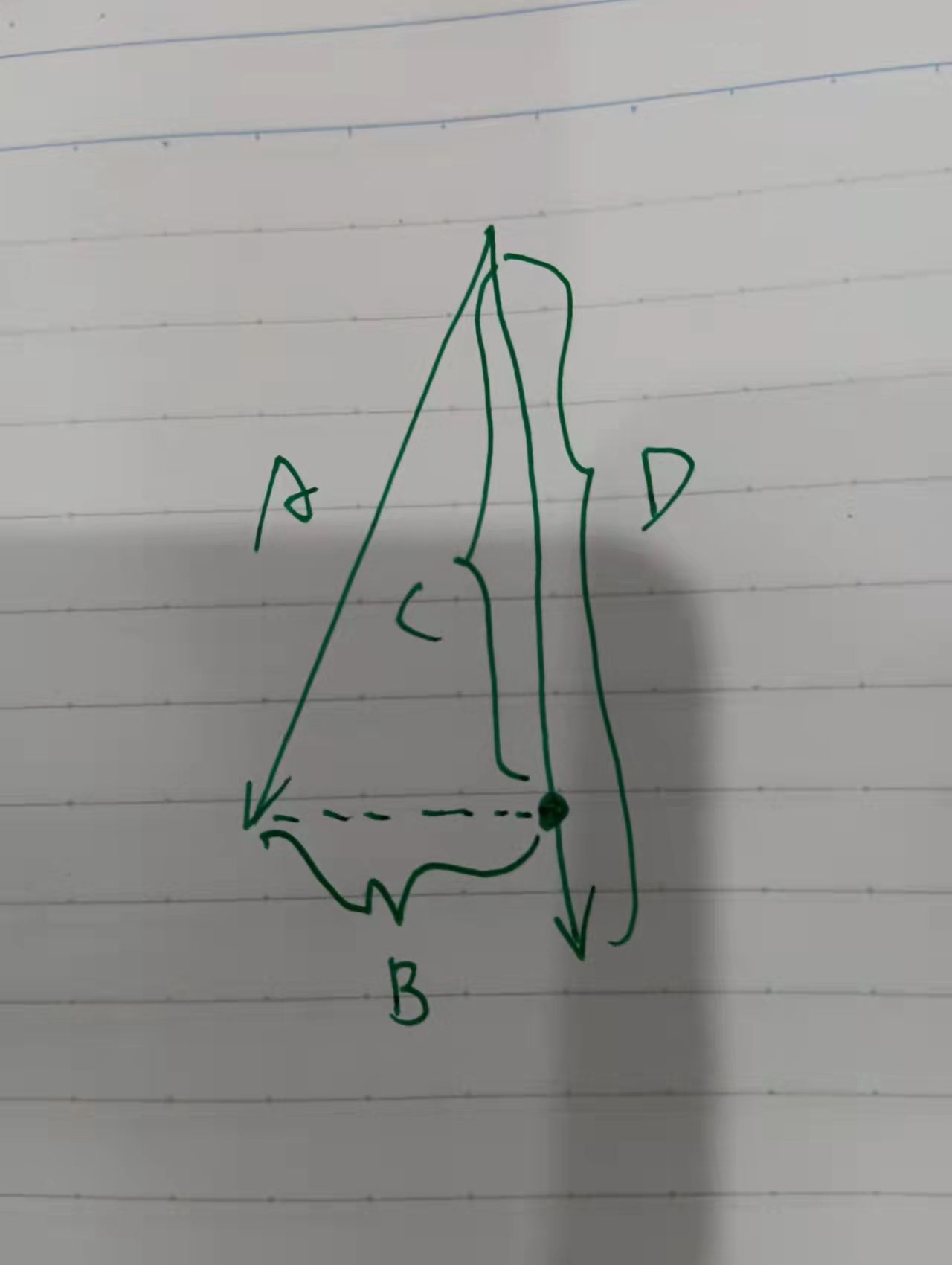
The procedure for limiting the angle is as follows: firstly, point multiply the Z-axis vector of the body and the unitized geographic Z-axis vector to obtain the cosine of the two vectors, then calculate the inverse cosine to obtain the tilt angle, and then limit the angle,

Body in the above program_ Unit corresponds to vector A, world in the figure below_ Unit corresponds to vector D in the figure below, (dot_product_unit * world_unit) corresponds to vector C in the figure below, and rejection corresponds to vector B in the figure below. Vector B is perpendicular to vector D. using vector D and unitized vector B, the thrust vector when the tilt angle reaches the maximum can be constructed through the maximum tilt angle angle, and finally assigned to the body_unit to limit the maximum tilt angle

Calculate the resultant force according to the hovering throttle

float collective_thrust = _acc_sp(2) * (_hover_thrust / CONSTANTS_ONE_G) - _hover_thrust;

The resultant force is used not only for hovering, but also for horizontal movement, so the tilt angle needs to be taken into account. Vector3f (0, 0, 1) Dot (body_z) calculates the cosine of the tilt angle by vector point multiplication, that is, the vertical component of the resultant force is always_ acc_ sp(2) * (_hover_thrust / CONSTANTS_ONE_G) - _ hover_ The horizontal component depends on the tilt angle

collective_thrust /= (Vector3f(0, 0, 1).dot(body_z));

Minimum thrust limit

collective_thrust = math::min(collective_thrust, -_lim_thr_min);

Seeking resultant force

_thr_sp = body_z * collective_thrust;
}