Before learning path calculation, we need a scene. We checked the maze generation method online and spent some time writing a simple maze generator
The basic principle is very simple:
The 2-dimensional matrix is used to represent the maze. Each node has four walls. The depth search is used to move in four directions randomly. If the node is reached, the direction will be stopped, and the wall between the two nodes will be eliminated. This can ensure that each node can be covered, and each node will have a way to the exit.

A simple algorithm has an obvious disadvantage: each node has only one fixed path, and there will be no multiple paths to a node.

The use of recursion in deep search is very concise and will not be repeated.
Specifically, where it is easy to suffer from pits, how to simply move up, down, left and right randomly, eliminate walls, and do not need a thousand if:
The first is the direction representation, which uses a list:
directions = [[0,-1],[1,0],[0,1],[-1,0]]
They represent upper right lower left respectively
Use random for [0,1,2,3] Shuffle () function, and then traverse the list to obtain the upper, lower, left and right vectors at random
Each node has four walls, expressed by [0,0,0,0], and the sequence direction is the same as the above direction.
When eliminating the wall between one node, you need to eliminate the node on the opposite side of the previous wall
Or operate on the direction. direction[i] expresses the direction vector. Here, the plus sign is to move to the right, rotate 45 degrees clockwise when moving one bit to the right, and rotate 45 degrees counterclockwise when moving one bit to the left
If the number i is shifted 2 bits to the right and projected onto 0-3, the direction can be changed.
Simply put, it is to move right and divide the remainder
During each search, if a node that has been accessed before is encountered, exit the function. The covered nodes are recorded in the function. If the total number of nodes is reached, exit directly
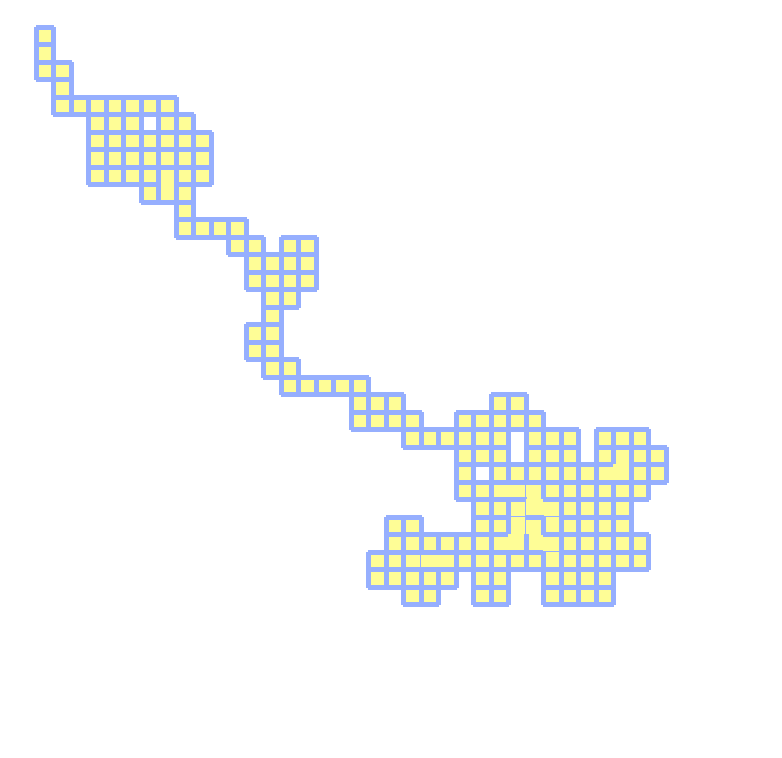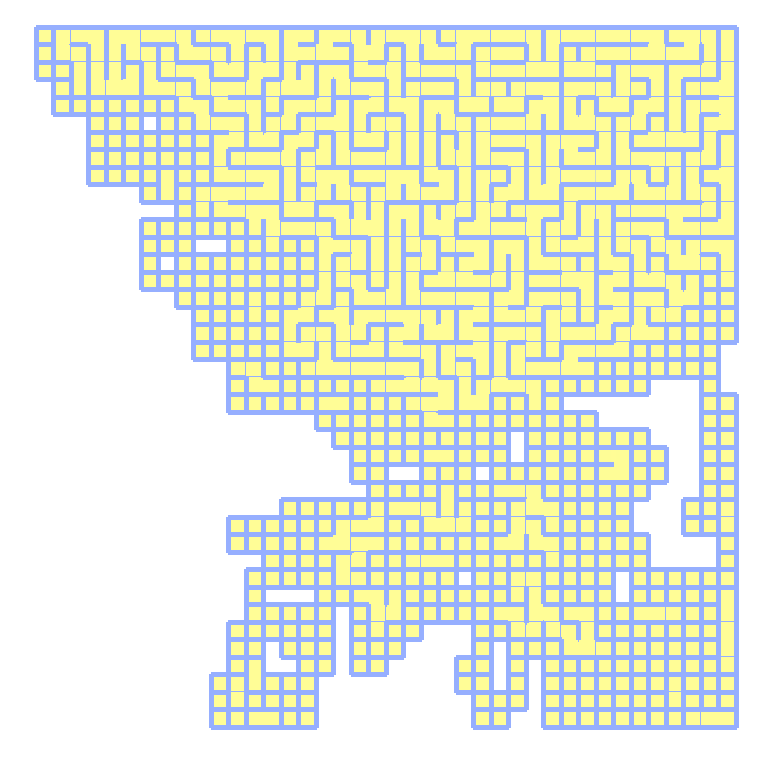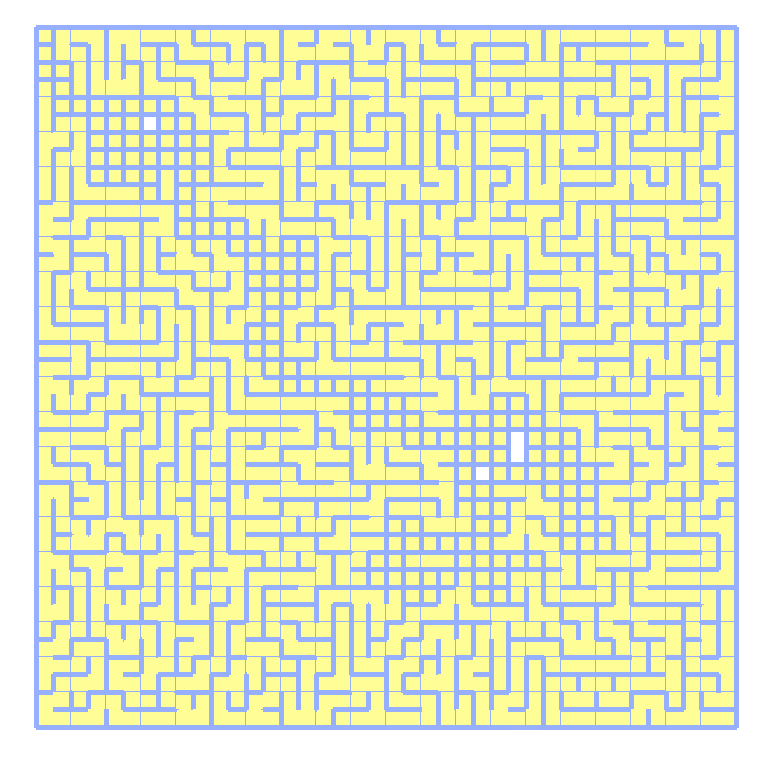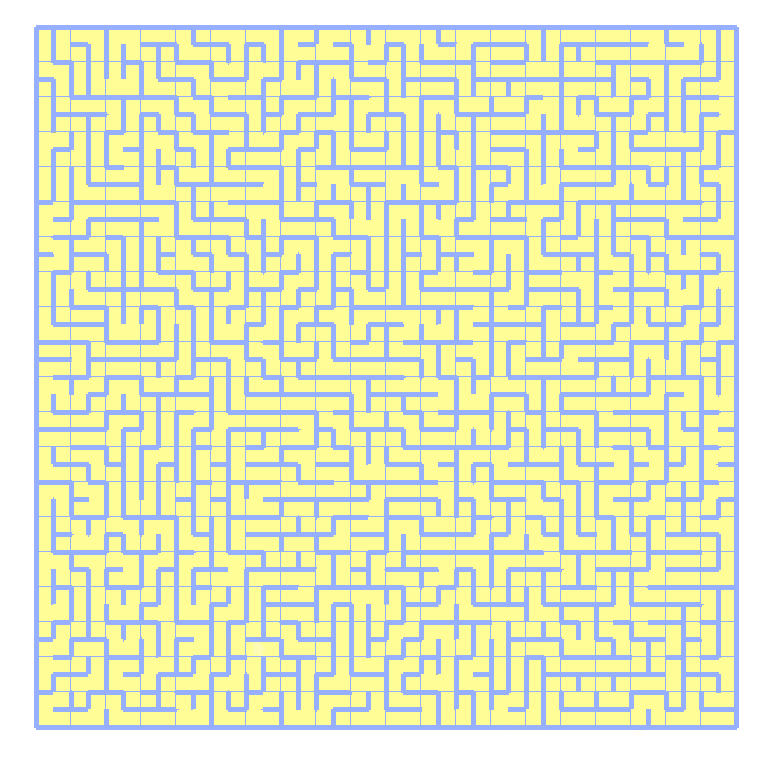
The operation effect is as follows:
We can see the characteristics of the recursive depth first algorithm: it will return to the previous node after the end of a road

import pygame as pg
import time
import random

class Tile():
    def __init__(self,grid_size,screen_size,x,y): #It mainly stores data and draws graphics, which has nothing to do with the algorithm
        self.x,self.y = x,y
        self.connected = [0,0,0,0] # up,right,down,left 0 for not connected
        self.grid_size = grid_size
        self.tile_size = [(screen_size[0]-100)/grid_size[0],(screen_size[1]-100)/grid_size[1]]
        self.rectangle = (self.x*self.tile_size[0]+50,self.y*self.tile_size[1]+50,self.tile_size[0],self.tile_size[1])
        self.points = [ [self.x*self.tile_size[0]+50,self.y*self.tile_size[1]+50],    #uppper left
                [self.x*self.tile_size[0]+50+self.tile_size[0],self.y*self.tile_size[1]+50],    #upper right
                [self.x*self.tile_size[0]+50+self.tile_size[0],self.y*self.tile_size[1]+50+self.tile_size[1]],    #lower right
                [self.x*self.tile_size[0]+50,self.y*self.tile_size[1]+50+self.tile_size[1]],    #lower left
                ] 
        self.visited = False

    def draw(self,color = (255,253,150)): #x,y represents the tile coordinates  
        pg.draw.rect(screen,color,self.rectangle)   #Draw node
        for i in range(4):  #Draw four walls
            if not self.connected[i]:
                pg.draw.line(screen,(150,175,255),(self.points[i]),(self.points[((i+1)%4)]),5)


def maze_gen(path):
    global tile_covered #Number of overlay nodes. When the number of overlay nodes reaches the number of grids, it will stop
    x,y = path[-1]
    if x < 0 or x >= grid_size[0] or y < 0 or y >= grid_size[1]:    #Exit if out of grid range
        print(f'index out of range at {x,y}')
        return
    matrix[y][x].draw()
    if matrix[y][x].visited:    #Exit if the node has been accessed
        print(f'node already visited at {x,y}')
        return
    elif tile_covered <= grid_size[0]*grid_size[1]: #The number of overlay nodes does not reach the total number of grids
        tile_covered += 1
        matrix[y][x].visited = True
        path_choice = [0,1,2,3]
        random.shuffle(path_choice)
        directions = [[0,-1],[1,0],[0,1],[-1,0]] # up,right,down,left 0 for not connected

        for i in path_choice:
            x_,y_ = x+directions[i][0],y+directions[i][1]
            path.append([x_,y_])
            if maze_gen(path):
                matrix[y][x].connected[i] = 1 #walls of current node
                matrix[y_][x_].connected[(i+2)%4] = 1#reverse the vector direction
                matrix[y][x].draw()
                matrix[y_][x_].draw()

            path.pop(-1)
        pg.display.update()


        return True

    else:
        print('all node visited')
        return


screen_size = [800,800]
grid_size = [40,40]
exit = [10,10]
tile_covered = 0
run = True

screen = pg.display.set_mode(screen_size)

matrix = []
for y in range(grid_size[1]):   #Create a two-dimensional matrix, where x and Y represent coordinates
    temp = []
    for x in range(grid_size[0]):
        tile = Tile(grid_size,screen_size,x,y)
        temp.append(tile)
    matrix.append(temp)

pg.init()
path = [[0,0]]

screen.fill((255,255,255))
maze_gen(path)

pg.display.update()

print('======== Generation Finished ========')
while run: #Do not exit after weighing, use the cycle
    for event in pg.event.get():
        if event.type == pg.QUIT:
            time.sleep(0.1)
            pg.quit()
            exit()