Data structures and algorithms

• Algorithm: methods and steps to solve problems

• Evaluate the quality of the algorithm: asymptotic time complexity and asymptotic space complexity.

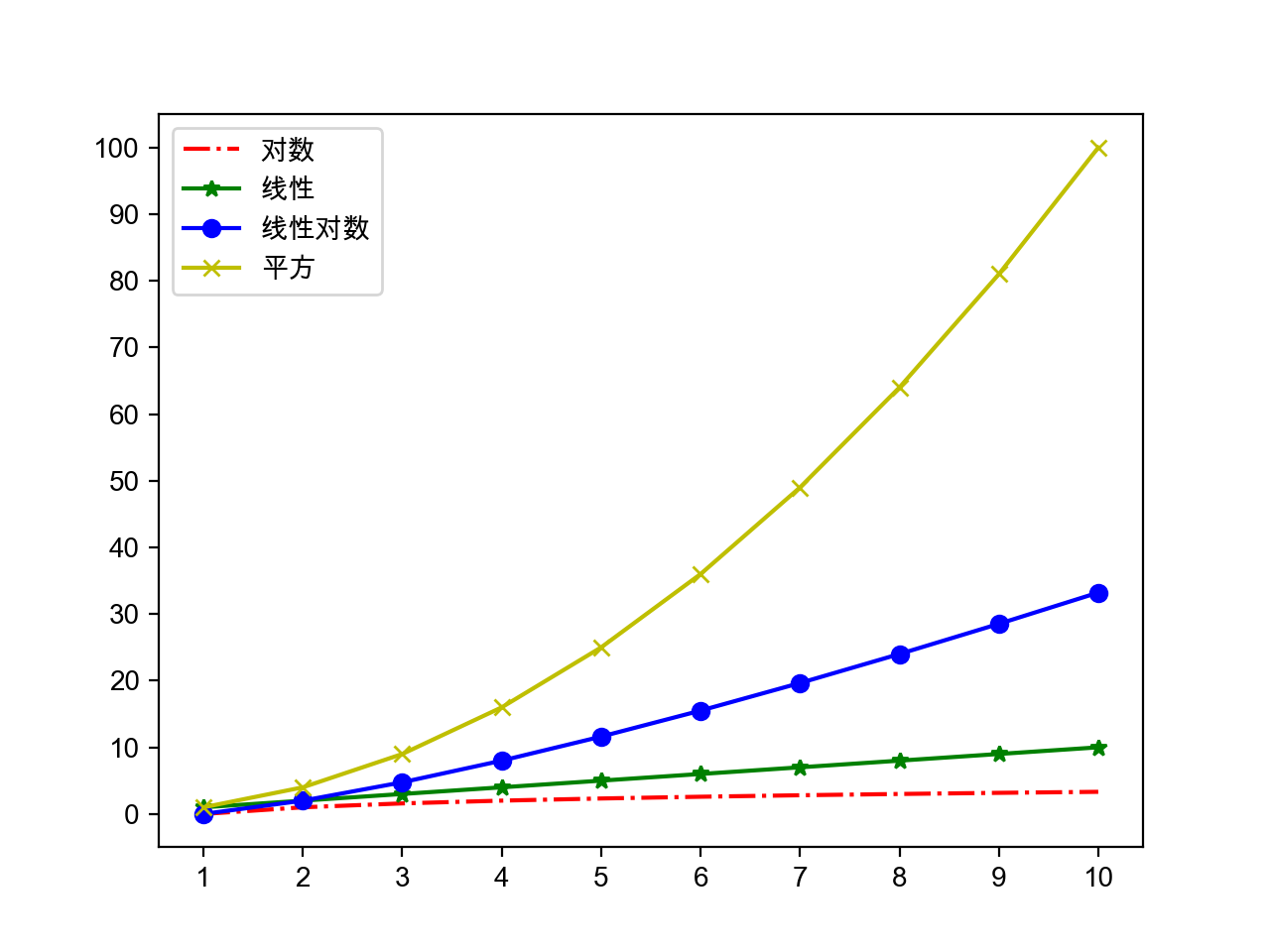
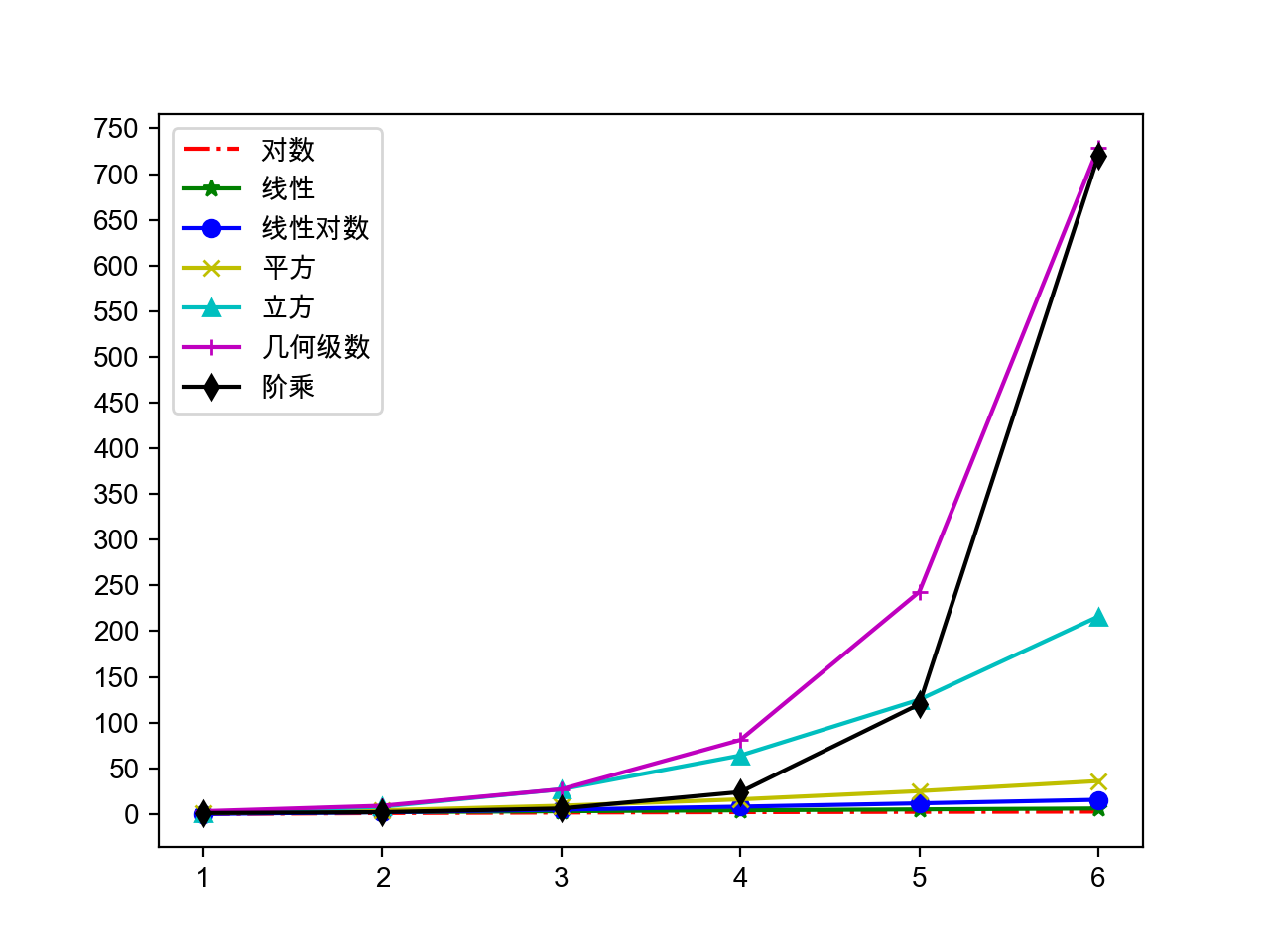
• Large O markers for asymptotic time complexity:

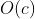  • -Constant time complexity - bloom filter / hash storage
  • -Logarithmic time complexity - half search (binary search)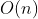
  • -Linear time complexity - sequential lookup / count sort
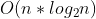  • -Log linear time complexity - Advanced sorting algorithm (merge sorting, quick sorting)
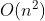  • -Square time complexity - simple sorting algorithm (selection sorting, insertion sorting, bubble sorting)
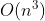  • -Cubic time complexity - Floyd algorithm / matrix multiplication
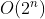  • -Geometric series time complexity - Tower of Hanoi
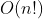  • -Factorial time complexity - Travel dealer problem - NPC

• Sorting algorithm (selection, bubbling and merging) and search algorithm (order and half)

  def select_sort(items, comp=lambda x, y: x < y):
      """Simple selection sort"""
      items = items[:]
      for i in range(len(items) - 1):
          min_index = i
          for j in range(i + 1, len(items)):
              if comp(items[j], items[min_index]):
                  min_index = j
          items[i], items[min_index] = items[min_index], items[i]
      return items
  

  def bubble_sort(items, comp=lambda x, y: x > y):
      """Bubble sorting"""
      items = items[:]
      for i in range(len(items) - 1):
          swapped = False
          for j in range(i, len(items) - 1 - i):
              if comp(items[j], items[j + 1]):
                  items[j], items[j + 1] = items[j + 1], items[j]
                  swapped = True
          if not swapped:
              break
      return items
  

  def bubble_sort(items, comp=lambda x, y: x > y):
      """Stirring sequencing(Bubble sort upgrade)"""
      items = items[:]
      for i in range(len(items) - 1):
          swapped = False
          for j in range(i, len(items) - 1 - i):
              if comp(items[j], items[j + 1]):
                  items[j], items[j + 1] = items[j + 1], items[j]
                  swapped = True
          if swapped:
              swapped = False
              for j in range(len(items) - 2 - i, i, -1):
                  if comp(items[j - 1], items[j]):
                      items[j], items[j - 1] = items[j - 1], items[j]
                      swapped = True
          if not swapped:
              break
      return items
  

  def merge(items1, items2, comp=lambda x, y: x < y):
      """merge(Merge two ordered lists into one ordered list)"""
      items = []
      index1, index2 = 0, 0
      while index1 < len(items1) and index2 < len(items2):
          if comp(items1[index1], items2[index2]):
              items.append(items1[index1])
              index1 += 1
          else:
              items.append(items2[index2])
              index2 += 1
      items += items1[index1:]
      items += items2[index2:]
      return items
  
  
  def merge_sort(items, comp=lambda x, y: x < y):
      return _merge_sort(list(items), comp)
  
  
  def _merge_sort(items, comp):
      """Merge sort"""
      if len(items) < 2:
          return items
      mid = len(items) // 2
      left = _merge_sort(items[:mid], comp)
      right = _merge_sort(items[mid:], comp)
      return merge(left, right, comp)
  

  def seq_search(items, key):
      """Sequential search"""
      for index, item in enumerate(items):
          if item == key:
              return index
      return -1
  

  def bin_search(items, key):
      """Half search"""
      start, end = 0, len(items) - 1
      while start <= end:
          mid = (start + end) // 2
          if key > items[mid]:
              start = mid + 1
          elif key < items[mid]:
              end = mid - 1
          else:
              return mid
      return -1
  

• Common algorithms:

  • Exhaustive method - also known as brute force cracking method, verifies all possibilities until the correct answer is found.
  • Greedy method - when solving a problem, always make a decision in the current view
  • The best choice is to find a satisfactory solution quickly without pursuing the optimal solution.
  • Divide and Conquer - divide a complex problem into two or more identical or similar subproblems, then divide the subproblem into smaller subproblems until it can be solved directly, and finally merge the solutions of the subproblems to obtain the solution of the original problem.
  • Backtracking method - backtracking method, also known as heuristic method, searches forward according to the optimization conditions. When it finds that the original selection is not excellent or fails to achieve the goal, it will go back to one step and choose again.
  • Dynamic programming - the basic idea is to decompose the problem to be solved into several sub problems, solve and save the solutions of these sub problems first, so as to avoid a large number of repeated operations.

  Examples of exhaustive method: 100 money, 100 chicken and five people share fish.

  # A rooster is 5 yuan, a hen is 3 yuan, a chick is 1 yuan and three
  # Buy 100 chickens for 100 yuan and ask how many cocks / hens / chicks each
  for x in range(20):
      for y in range(33):
          z = 100 - x - y
          if 5 * x + 3 * y + z // 3 == 100 and z % 3 == 0:
              print(x, y, z)
  
  # A. B, C, D and E went fishing together one night, and finally they were tired and went to bed
  # The next day A woke up first. He divided the fish into five parts, threw away the extra one and took one of his own
  # B the second one wakes up and divides the fish into five parts. Throw away the extra one and take one of his own
  # Then C, D and E woke up in turn and divided the fish in the same way. They asked how many fish they had caught at least
  fish = 6
  while True:
      total = fish
      enough = True
      for _ in range(5):
          if (total - 1) % 5 == 0:
              total = (total - 1) // 5 * 4
          else:
              enough = False
              break
      if enough:
          print(fish)
          break
      fish += 5
  

  Example of greedy method: suppose the thief has a backpack that can hold up to 20 kilograms of stolen goods. He breaks into a house and finds the items shown in the table below. Obviously, he can't put all his items in his backpack, so he must determine what items to take away and what items to leave behind.

  name	Price (USD)	Weight (kg)
  computer	200	20
  radio	20	4
  clock	175	10
  vase	50	2
  book	10	1
  Oil Painting	90	9

  """
  Greedy method: when solving problems, we always make the best choice at present, do not pursue the optimal solution, and quickly find a satisfactory solution.
  Input:
  20 6
   Computer 200 20
   Radio 20 4
   Clock 175 10
   Vase 50 2
   Book 10 1
   Oil painting 90 9
  """
  class Thing(object):
      """goods"""
  
      def __init__(self, name, price, weight):
          self.name = name
          self.price = price
          self.weight = weight
  
      @property
      def value(self):
          """Price weight ratio"""
          return self.price / self.weight
  
  
  def input_thing():
      """Enter item information"""
      name_str, price_str, weight_str = input().split()
      return name_str, int(price_str), int(weight_str)
  
  
  def main():
      """Main function"""
      max_weight, num_of_things = map(int, input().split())
      all_things = []
      for _ in range(num_of_things):
          all_things.append(Thing(*input_thing()))
      all_things.sort(key=lambda x: x.value, reverse=True)
      total_weight = 0
      total_price = 0
      for thing in all_things:
          if total_weight + thing.weight <= max_weight:
              print(f'The thief took it{thing.name}')
              total_weight += thing.weight
              total_price += thing.price
      print(f'Total value: {total_price}dollar')
  
  
  if __name__ == '__main__':
      main()
  

  Examples of divide and Conquer: Quick sort.

  """
  Quick sort - Select the pivot to divide the elements. The left is smaller than the pivot and the right is larger than the pivot
  """
  def quick_sort(items, comp=lambda x, y: x <= y):
      items = list(items)[:]
      _quick_sort(items, 0, len(items) - 1, comp)
      return items
  
  
  def _quick_sort(items, start, end, comp):
      if start < end:
          pos = _partition(items, start, end, comp)
          _quick_sort(items, start, pos - 1, comp)
          _quick_sort(items, pos + 1, end, comp)
  
  
  def _partition(items, start, end, comp):
      pivot = items[end]
      i = start - 1
      for j in range(start, end):
          if comp(items[j], pivot):
              i += 1
              items[i], items[j] = items[j], items[i]
      items[i + 1], items[end] = items[end], items[i + 1]
      return i + 1
  

  Example of backtracking method: Knight patrol.

  """
  Recursive backtracking method: it is called heuristic method. It searches forward according to the optimization conditions. When it is found that the original selection is not optimal or cannot reach the goal, it will go back and make a new selection. The more classic problems include Knight patrol, eight queens and maze routing.
  """
  import sys
  import time
  
  SIZE = 5
  total = 0
  
  
  def print_board(board):
      for row in board:
          for col in row:
              print(str(col).center(4), end='')
          print()
  
  
  def patrol(board, row, col, step=1):
      if row >= 0 and row < SIZE and \
          col >= 0 and col < SIZE and \
          board[row][col] == 0:
          board[row][col] = step
          if step == SIZE * SIZE:
              global total
              total += 1
              print(f'The first{total}Seed walking method: ')
              print_board(board)
          patrol(board, row - 2, col - 1, step + 1)
          patrol(board, row - 1, col - 2, step + 1)
          patrol(board, row + 1, col - 2, step + 1)
          patrol(board, row + 2, col - 1, step + 1)
          patrol(board, row + 2, col + 1, step + 1)
          patrol(board, row + 1, col + 2, step + 1)
          patrol(board, row - 1, col + 2, step + 1)
          patrol(board, row - 2, col + 1, step + 1)
          board[row][col] = 0
  
  
  def main():
      board = [[0] * SIZE for _ in range(SIZE)]
      patrol(board, SIZE - 1, SIZE - 1)
  
  
  if __name__ == '__main__':
      main()
  

  Dynamic programming example: the maximum value of the sum of sub list elements.

  Note: sublist refers to the list composed of elements with continuous indexes (subscripts) in the list; The elements in the list are of type int and may contain positive integers, 0 and negative integers; The program inputs the elements in the list and outputs the maximum value of the summation of sub list elements, for example:

  Input: 1 - 2 3 5 - 3 2

  Output: 8

  Input: 0 - 2 3 5 - 1 2

  Output: 9

  Input: - 9 - 2 - 3 - 5 - 3

  Output: - 2

  def main():
      items = list(map(int, input().split()))
      overall = partial = items[0]
      for i in range(1, len(items)):
          partial = max(items[i], partial + items[i])
          overall = max(partial, overall)
      print(overall)
  
  
  if __name__ == '__main__':
      main()
  

  Note: the easiest solution to this problem is to use double loops, but the time performance of the code will become very bad. Using the idea of dynamic programming, only two more variables are used O ( N 2 ) O(N^2) The problem of O(N2) complexity becomes O ( N ) O(N) O(N).