Unknowingly, today and Friday, 513330 is almost breaking 6, and the inverted pyramid and warehouse are added to the basement. I'm really convinced.

In the previous tutorials, we played some strange things. Today, let's play a serious thing and draw a five-star red flag, that is, our national flag.

If you don't have any gossip, first put on the finished product drawing.

If you don't say much, go to the tutorial.

Flag and Mathematics

Before drawing the national flag, we need to understand the graphic structure of the national flag.

According to the explanation on the national flag system law issued by the presidium of the first plenary session of the Chinese people's Political Consultative Conference on September 28, 1949, the national flag of the people's Republic of China is red and rectangular, its length and height are three to two, and five yellow five pointed stars are decorated at the top left of the flag. One star is larger, its circumscribed circle diameter is three tenths of the flag height, ranking on the left; The four stars are small, with a circumscribed circle diameter of one tenth of the flag height, and the ring arch is to the right of the big star. The flagpole cover is white. The red of the national flag of the people's Republic of China symbolizes the revolution. The five five pointed stars on the flag and their relationship symbolize the great unity of the revolutionary people under the leadership of the Communist Party. The five pointed stars use yellow to show light on the red ground. Yellow is brighter and more beautiful than white. Each of the four small five pointed stars has a tip facing the center of the big star, which means that they are united around a center and appear compact and beautiful in form.

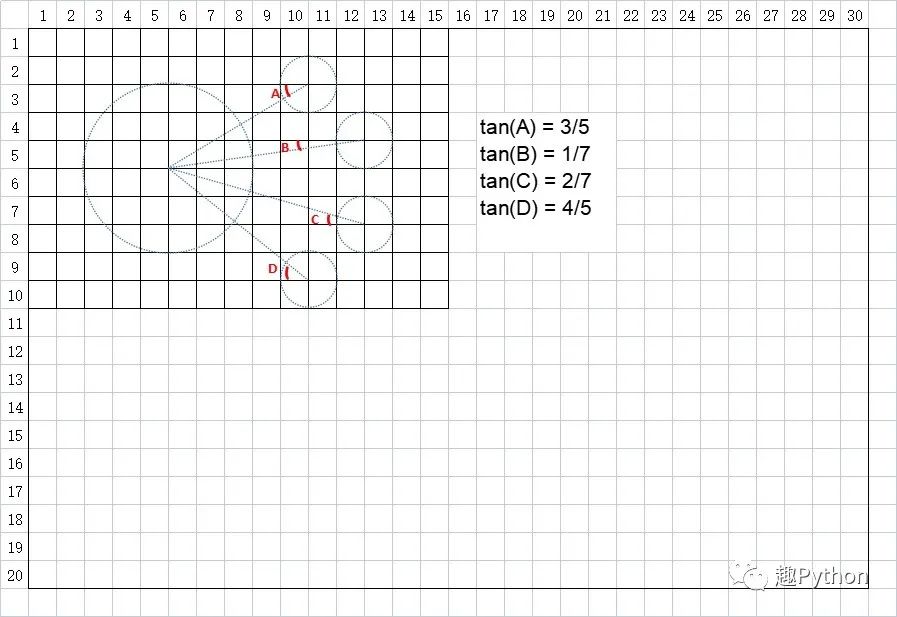
As shown in the figure below:

We convert it into a mathematical relationship (assuming that the center point of the national flag is the origin of the coordinate system (0,0), and the length and width of each lattice is L):

1. The four vertices of the national flag are (- 15L,10L), (15L,10L), (15L,-10L), (- 15L,-10L)
2. The center point of the big Pentagram is (- 10L,5L), the radius is 3L, and it is placed horizontally
3. The center point of small Pentagram A is (- 5L,8L), the radius is l, tan(A)=3/5
4. The center point of small Pentagram B is (- 3L,6L), the radius is l, tan(B)=1/7
5. The center point of pentagonal C is (- 3L,3L), the radius is l, tan(C)=2/7
6. The center point of small pentagonal star D is (- 5L,1L), the radius is l, tan(A)=4/5

This is the basis of our later drawing. Let's put it here first.

Start drawing

Let's draw the flag first. It's a simple rectangle. The idea is very simple:

1. Start from the top left vertex, go east, seth(0), and walk a length of 30L.
2. Further south, seth(-90), take the length of 20L.
3. Further west, seth(180), take a length of 30L.
4. Finally, go north, seth(90), take a length of 20L.
5. fill is red.

The code is as follows:

def rectangle(center, length_x, length_y, penc, fillc):
    turtle.pensize(1)
    turtle.fillcolor(fillc)
    turtle.pencolor(penc)
    turtle.up()
    pos=(center[0]-length_x/2, center[1]+length_y/2)
    turtle.goto(pos)
    turtle.begin_fill()
    turtle.down()
    turtle.seth(0)
    turtle.fd(length_x)
    turtle.seth(-90)
    turtle.fd(length_y)
    turtle.seth(180)
    turtle.fd(length_x)
    turtle.seth(90)
    turtle.fd(length_y)
    turtle.end_fill()

Then draw a five pointed star. Let's decompose it first and draw a positive five pointed star.

Similarly, let's figure out the mathematical relationship first, as shown in the figure below:

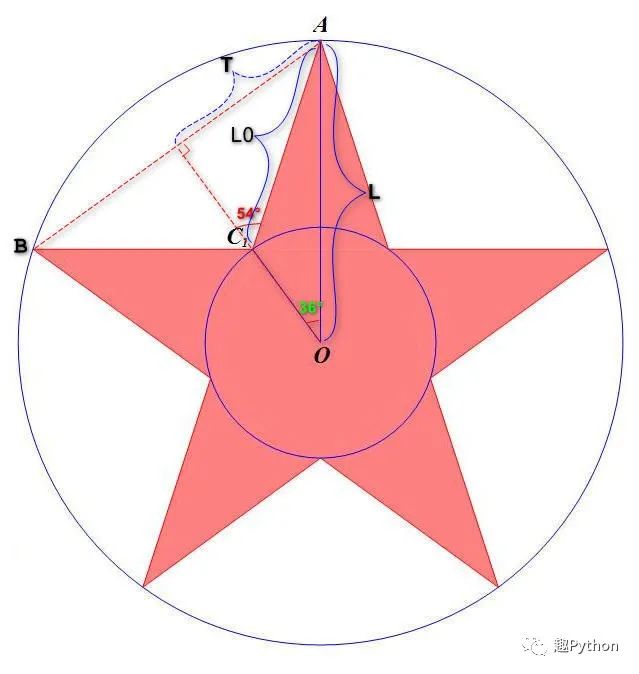
Suppose the radius of the circle is L.

Let's find the side length relationship first, because: sin(54) = T / L0 and sin(36) = T / L, we get: L0 = L * sin(36) / sin(54), that is, the side length of the pentagram.

We observe that the edges of the pentagram are reproducible. A-C1-B can be drawn five times, so let's draw A-C1-B first.

1. Don't write yet. Start from O, go north, seth(90), take the length of L, and now it's at point A.
2. Southwest, seth(180+72), get ready.
3. Write down and walk the length of L0 to point C1.
4. Turn right 72 degrees and go the length of L0 to point B.
5. So far, A-C1-B has been drawn.
6. Then we turn the direction to the next drawing direction, turn left 144 degrees, left(144).
7. Repeat the actions of 3-6 for 4 times to complete the whole figure.
8. Finally, fill is yellow.

The code is as follows:

def star(pos, length, penc, fillc):
    turtle.pensize(1)
    turtle.fillcolor(fillc)
    turtle.pencolor(penc)
    L = length*math.sin(36*math.pi/180)/math.sin(54*math.pi/180)
    turtle.up()
    turtle.goto(pos)
    turtle.seth(90)
    turtle.fd(length)
    turtle.seth(180+72)
    turtle.down()
    turtle.begin_fill()
    for _ in range(5):
        turtle.fd(L)
        turtle.right(72)
        turtle.fd(L)
        turtle.left(144)
    turtle.end_fill()

We have drawn the pentagram. Now we need to rotate it at an angle.

At this time, we found that during the drawing process, the angle of the pentagram had been adjusted before the down, and the five broken lines were all relative positions.

OK, let's change the function:

def star(pos, angle, length, penc, fillc):
    turtle.pensize(1)
    turtle.fillcolor(fillc)
    turtle.pencolor(penc)
    L = length*math.sin(36*math.pi/180)/math.sin(54*math.pi/180)
    turtle.up()
    turtle.goto(pos)
    turtle.seth(90+angle)
    turtle.fd(length)
    turtle.seth(180+72+angle)
    turtle.down()
    turtle.begin_fill()
    for _ in range(5):
        turtle.fd(L)
        turtle.right(72)
        turtle.fd(L)
        turtle.left(144)
    turtle.end_fill()

Again, rotate 20 °:

star((0, 0), 0, 90, 'yellow', 'yellow')
star((150, 0), 20, 90, 'red', 'red')

OK, here, everything is ready, just the code.

Draw the national flag

All the details are clear, go directly to the code!!!

#coding: utf-8

import turtle
import time
import math

turtle.setup(width=1.0, height=1.0, startx=None, starty=None)
turtle.ht()
turtle.tracer(0, 0)
turtle.bgcolor("black")

turtle.pensize(1)

def star(center, angle, length, penc, fillc):
    turtle.pensize(1)
    turtle.fillcolor(fillc)
    turtle.pencolor(penc)
    L = length*math.sin(36*math.pi/180)/math.sin(54*math.pi/180)    
    turtle.up()
    turtle.goto(center)
    turtle.seth(90+angle)
    turtle.fd(length)
    turtle.seth(180+72+angle)
    turtle.down()
    turtle.begin_fill()
    for _ in range(5):
        turtle.fd(L)
        turtle.right(72)
        turtle.fd(L)
        turtle.left(144)
    turtle.end_fill()

def rectangle(center, length_x, length_y, penc, fillc):
    turtle.pensize(1)
    turtle.fillcolor(fillc)
    turtle.pencolor(penc)
    turtle.up()
    pos=(center[0]-length_x/2, center[1]+length_y/2)
    turtle.goto(pos)
    turtle.begin_fill()
    turtle.down()
    turtle.seth(0)
    turtle.fd(length_x)
    turtle.seth(-90)
    turtle.fd(length_y)
    turtle.seth(180)
    turtle.fd(length_x)
    turtle.seth(90)
    turtle.fd(length_y)
    turtle.end_fill()

W = 1200
H = 800
dW = W/30
dH = H/20

#time.sleep(6)

rectangle((0,0), W, H, 'red', 'red')
C0 = (-dW*10, dH*5)
A0 = 0
L0 = dW*3
star(C0, A0, L0, 'yellow', 'yellow')
C1 = (-dW*5, dH*8)
A1 = 90+math.atan(3/5)*180/math.pi
L1 = dW
star(C1, A1, L1, 'yellow', 'yellow')
C2 = (-dW*3, dH*6)
A2 = 90+math.atan(1/7)*180/math.pi
L2 = dW
star(C2, A2, L2, 'yellow', 'yellow')
C3 = (-dW*3, dH*3)
A3 = 90-math.atan(2/7)*180/math.pi
L3 = dW
star(C3, A3, L3, 'yellow', 'yellow')
C4 = (-dW*5, dH)
A4 = 90-math.atan(4/5)*180/math.pi
L4 = dW
star(C4, A4, L4, 'yellow', 'yellow')