Arrays and linked lists
Array features
1. Continuous: sequential storage.
2. Fixed length: once defined, the length cannot be changed.
3. According to the subscript, you can directly access the elements of this subscript.
4. It is not suitable for inserting, deleting and other operations.
In python, the list is a dynamic array
Linked list features
1. It can be discontinuous.
2. Variable length.
3. You cannot access directly according to the subscript. You must look back one by one.
4. It is suitable for inserting, deleting and other operations.
Queues and stacks
queue
Queue characteristics
1. First in first out
2. Data can only be inserted from the end of the queue
3. Data can only be retrieved from the queue header
class Queue(object):
def __init__(self):
self.data_list = []
def init_queue(self):
self.data_list = []
def insert(self, data):
self.data_list.append(data)
def pop(self):
if len(self.data_list) == 0:
return None
data = self.data_list[0]
del self.data_list[0]
return data
def size(self):
return len(self.data_list)
queue = Queue()
print(queue.size())
queue.insert(1)
queue.insert(2)
queue.insert(3)
head = queue.pop()
print(head)
head = queue.pop()
print(head)
head = queue.pop()
print(head)
head = queue.pop()
print(head)
Stack
Stack features
1. Last in first out.
2. Data can only be inserted from the tail.
3. Data can only be taken from the tail.
class Stack(object):
def __init__(self):
self.data_stack = []
def init_Stack(self):
self.data_stack = []
def insert(self, data):
self.data_stack.append(data)
def pop(self):
if len(self.data_stack) == 0:
return None
data = self.data_stack[-1]
del self.data_stack[-1]
return data
def size(self):
return len(self.data_stack)
stack = Stack()
stack.insert(1)
stack.insert(2)
stack.insert(3)
tail = stack.pop()
print(tail)
tail = stack.pop()
print(tail)
tail = stack.pop()
print(tail)
tail = stack.pop()
print(tail)
tree
Many trees form a forest.
Binary tree
A binary tree is a tree in which each node has at most two child nodes.
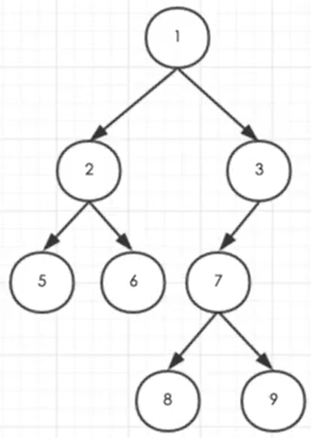
Preorder traversal (left and right roots)
Preorder traversal order:
[1, 2, 5, 6, 3, 7, 8, 9]
Middle order traversal (left root right)
Middle order traversal order:
[5, 2, 6, 1, 8, 7, 9, 3]
Postorder traversal (left and right roots)
Post traversal order:
[ 5, 6, 2, 8, 9, 7, 3, 1]
Implementation of binary tree in python
class Node(object):
def __init__(self, index):
self.index = index
self.left_child = None
self.right_child = None
class BinaryTree(object):
def __init__(self, root):
self.root = root
# Preamble
def pre_travel(self, node):
if not node:
return
print(node.index)
self.pre_travel(node.left_child)
self.pre_travel(node.right_child)
# Middle order
def inner_travel(self, node):
if not node:
return
self.inner_travel(node.left_child)
print(node.index)
self.inner_travel(node.right_child)
# Post order
def order_travel(self, node):
if not node:
return
self.order_travel(node.left_child)
self.order_travel(node.right_child)
print(node.index)
if __name__ == '__main__':
node_dict = {}
for i in range(1, 10):
node_dict[i] = Node(i)
node_dict[1].left_child = node_dict[2]
node_dict[1].right_child = node_dict[3]
node_dict[2].left_child = node_dict[5]
node_dict[2].right_child = node_dict[6]
node_dict[3].left_child = node_dict[7]
node_dict[7].left_child = node_dict[8]
node_dict[7].right_child = node_dict[9]
tree = BinaryTree(node_dict[1])
tree.pre_travel(node_dict[1])
tree.inner_travel(node_dict[1])
tree.order_travel(node_dict[1])
sort
Sorting algorithm
Insert sort
Insert the original array into the new sorted array
Bubble sorting
exchange
Quick sort (most classic)
Select a benchmark value
def quick_sort(origin_list, start, end):
if start >= end:
return
left = start
right = end
flag_index = left
while left < right:
while right > left:
if origin_list[right] < origin_list[flag_index]:
origin_list[right], origin_list[flag_index] = origin_list[flag_index], origin_list[right]
flag_index = right
break
right -= 1
while left < right:
if origin_list[left] > origin_list[flag_index]:
origin_list[left], origin_list[flag_index] = origin_list[flag_index], origin_list[left]
flag_index = left
break
left += 1
quick_sort(origin_list, start, flag_index)
quick_sort(origin_list, flag_index + 1, end)
origin_list = [5, 3, 1, 7, 9, 8]
quick_sort(origin_list, 0, len(origin_list) - 1)
print(origin_list)
Merge sort
Each time is divided into two parts, two in life, two in four, four in eight. Sort each part, and then merge them together.
Binary search
Implementation of binary search in python
def binary_search(search_list, target):
left = 0
right = len(search_list) - 1
while left <= right:
mid = left + (right-left) // 2
if search_list[mid] < target:
left = mid + 1
continue
if search_list[mid] == target:
return mid
if search_list[mid] > target:
right = mid - 1
return None
search_list = [1, 3, 4, 6, 8, 9]
print(binary_search(search_list, 5))
print(binary_search(search_list, 1))
print(binary_search(search_list, 3))
print(binary_search(search_list, 4))
print(binary_search(search_list, 6))
print(binary_search(search_list, 8))
print(binary_search(search_list, 9))
heap
Heap characteristics
1. Heap is a binary tree.
2. Leaf nodes only exist in the lowest two layers.
3. From the root node to the penultimate layer, it is a complete binary tree.
4. A node cannot have only right children.
5. The left and right children of a node are larger (or smaller) than this node
For example – large top pile:
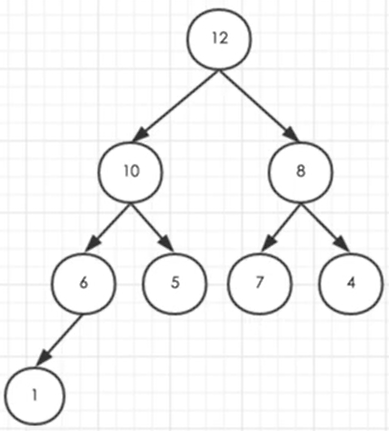
Heap python implementation
class Heap(object):
def __init__(self):
self.data_list = [None]
def size(self):
return len(self.data_list) - 1
def left_child(self, root):
return root * 2
def right_child(self, root):
return root * 2 + 1
def father(self, node):
return node // 2
# Maintain heap status
def heapify(self, root):
if root > self.size():
return
left_node = self.left_child(root)
right_node = self.right_child(root)
largest = root
if left_node <= self.size():
if self.data_list[left_node] >self.data_list[largest]:
largest = left_node
if right_node <= self.size():
if self.data_list[right_node] > self.data_list[largest]:
largest = right_node
if largest != root:
self.data_list[root], self.data_list[largest] = self.data_list[largest], self.data_list[root]
self.heapify(largest)
# Build a heap (the last non leaf node is where the size of the heap is divided by two)
def build_heap(self):
for i in range(self.size()//2, 0, -1):
self.heapify(i)
# Take the top of the pile
def get_max(self):
if self.size() == 0:
return None
ret = self.data_list[1]
self.data_list[1] = self.data_list[-1]
del self.data_list[-1]
self.heapify(1)
return ret
def insert(self, data):
self.data_list.append(data)
now_index = self.size()
pre = self.father(now_index)
while now_index != 1 and self.data_list[pre] < data:
self.data_list[pre], self.data_list[now_index] = self.data_list[now_index], self.data_list[pre]
now_index = pre
pre = self.father(now_index)
if __name__ == '__main__':
heap = Heap()
heap.insert(9)
heap.insert(10)
heap.insert(7)
heap.insert(12)
heap.insert(3)
heap.insert(4)
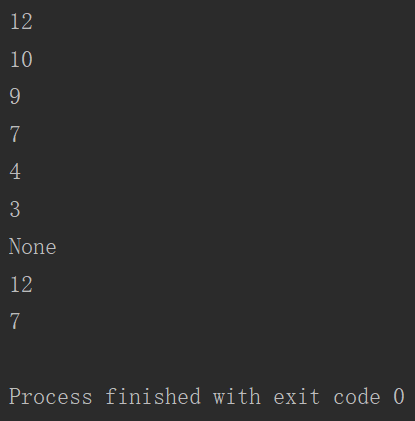
print(heap.get_max())
print(heap.get_max())
print(heap.get_max())
print(heap.get_max())
print(heap.get_max())
print(heap.get_max())
print(heap.get_max())
heap.insert(10)
heap.insert(9)
heap.insert(8)
heap.insert(7)
heap.insert(7)
heap.insert(12)
print(heap.get_max())
heap.data_list = [None, 1, 2, 3, 4, 5, 6, 7]
heap.build_heap()
print(heap.get_max())
Running results