56. Tree and tree algorithm

Concept of tree

Tree (English: tree) is an abstract data type (ADT) or a data structure that implements this abstract data type. It is used to simulate a data set with tree structure. It is a set with hierarchical relationship composed of n (n > = 1) finite nodes. It is called "tree" Because it looks like an upside down tree, that is, it has roots up and leaves down. It has the following characteristics:

• Each node has zero or more child nodes;
• A node without a parent node is called a root node;
• Each non root node has only one parent node;
• In addition to the root node, each child node can be divided into multiple disjoint subtrees;

  

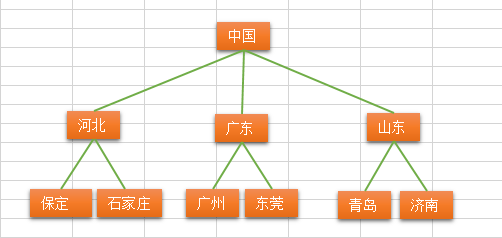
Tree terms

• Node degree: the number of subtrees contained in a node is called the degree of the node;
• Tree degree: the degree of the largest node in a tree is called the degree of the tree;
• Leaf node or terminal node: node with zero degree;
• Parent node or parent node: if a node contains child nodes, this node is called the parent node of its child nodes;
• Child node or child node: the root node of the subtree contained in a node is called the child node of the node;
• Sibling node: nodes with the same parent node are called sibling nodes;
• Node hierarchy: defined from the root, the root is the first layer, and the child node of the root is the second layer, and so on;
• Height or depth of tree: the maximum level of nodes in the tree;
• Cousin node: nodes in the same layer as parent nodes are cousins to each other;
• Ancestor of a node: all nodes from the root to the branch through which the node passes;
• Descendant: any node in the subtree with a node as the root is called the descendant of the node.
• Forest: a collection of m (m > = 0) disjoint trees is called forest;

Tree species

• Unordered tree: there is no sequential relationship between the child nodes of any node in the tree. This tree is called unordered tree, also known as free tree;
• Ordered tree: there is a sequential relationship between the child nodes of any node in the tree, which is called ordered tree;
  • Binary tree: a tree with at most two subtrees per node is called a binary tree;
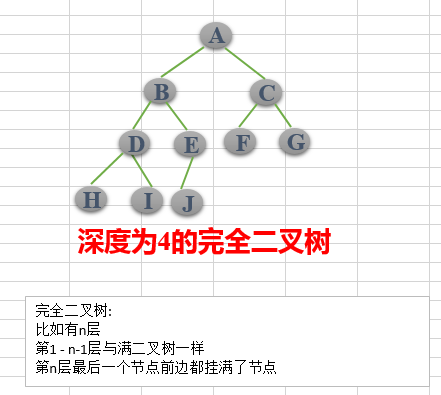
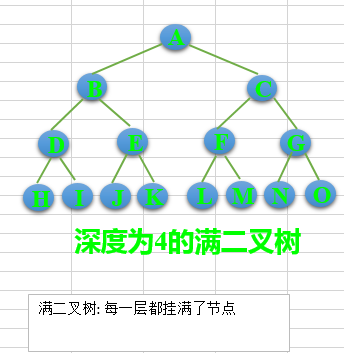
    • Complete binary tree: for a binary tree, suppose its depth is d (d > 1). Except for layer D, the number of nodes in other layers has reached the maximum, and all nodes in layer D are continuously and closely arranged from left to right. Such a binary tree is called a complete binary tree, in which the definition of full binary tree is a complete binary tree in which all leaf nodes are at the bottom;
    • Balanced binary tree (AVL tree): if and only if the height difference between two subtrees of any node is not greater than 1;
    • Sorted binary tree (Binary Search Tree, also known as Binary Search Tree and ordered binary tree);
  • Huffman tree (for information coding): the binary tree with the shortest weighted path is called Huffman tree or optimal binary tree;
  • B-tree: a self balanced binary search tree that optimizes read and write operations. It can keep data in order and has more than two subtrees.

Storage and representation of tree

Sequential storage: storing the data structure in a fixed array has certain advantages in traversal speed, but it is a non mainstream binary tree due to its large space. Binary trees are usually stored in chains.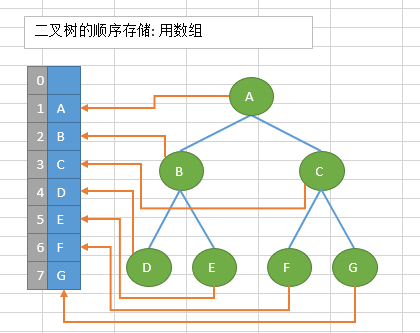  

Chained storage:

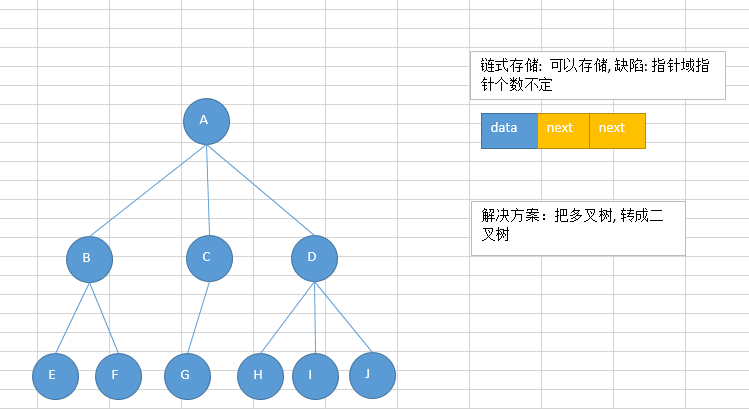
Because the number of nodes cannot be mastered, the storage representations of common trees are converted into binary trees for processing, and the maximum number of child nodes is 2

Some common tree application scenarios

1.xml, html, etc. when writing parsers for these things, it is inevitable to use trees
2. Routing protocol is an algorithm using tree
3.mysql database index
4. Directory structure of file system
5. Therefore, many classical AI algorithms are actually tree search. In addition, the decision tree in machine learning is also a tree structure

57. Concept of binary tree

Basic concepts of binary tree

A binary tree is a tree structure in which each node has at most two subtrees. Subtrees are usually called "left subtree" and "right subtree"

Properties of binary tree

Property 1: there are at most 2^(i-1) nodes (I > 0) on layer I of binary tree
Property 2: a binary tree with depth K has at most 2^k - 1 nodes (k > 0)
Property 3: for any binary tree, if the number of leaf nodes is N0 and the total number of nodes with degree 2 is N2, then N0=N2+1;
Property 4: the depth of a complete binary tree with n nodes must be log2(n+1)
Property 5: for a complete binary tree, if it is numbered from top to bottom and from left to right, the left child number of the node numbered i must be 2i and the right child number must be 2i + 1; The number of its parents must be i/2 (when i = 1, it is the root, except)

 

58. Breadth first traversal of binary tree

Node representation of binary tree and creation of tree

class Node(object):
    """Node class"""
    def __init__(self, item):
        self.item = item
        self.lchild = None
        self.rchild = None

class Tree(object):
    """Tree class"""
    def __init__(self):
        self.root = None

59. Implementation of binary tree

Implementation of binary tree

class Node(object):
    """Node class"""
    def __init__(self, item):
        self.item = item
        self.lchild = None
        self.rchild = None

class Tree(object):
    """Tree class"""
    def __init__(self):
        self.root = None

    def add(self,item):
        node = Node(item)
        if self.root is None:
            self.root = node
            return
        queue = [self.root]
        while queue:
            cur_node = queue.pop(0)
            if cur_node.lchild is None:
                cur_node.lchild = node
                return
            else:
                queue.append(cur_node.lchild)
            if cur_node.rchild is None:
                cur_node.rchild = node
                return
            else:
                queue.append(cur_node.rchild)

60. First order, middle order and last order traversal of binary tree

Breadth first traversal (level traversal)

Starting from the root of the tree, traverse the nodes of the whole tree from top to bottom and from left to right

def breadth_travel(self):
    """Hierarchical traversal of tree using queue"""
    if self.root is None:
        return
    queue = [self.root]
    while queue:
        cur_node = queue.pop(0)
        print(cur_node.item)
        if cur_node.lchild is not None:
            queue.append(cur_node.lchild)
        if cur_node.rchild is not None:
            queue.append(cur_node.rchild)    

if __name__ == "__main__":
    tree = Tree()
    tree.add(1)
    tree.add(2)
    tree.add(3)
    tree.add(4)
    tree.add(5)
    tree.breadth_travel()

1
2
3
4
5

Depth first traversal

For a binary tree, depth first search is to traverse the nodes of the tree along the depth of the tree and search the branches of the tree as deep as possible.
Then there are three important methods for depth traversal. These three methods are often used to access the nodes of the tree. The difference between them is that the order of accessing each node is different. These three kinds of traversal are called preorder, inorder and postorder respectively. Let's give their detailed definitions, and then take an example to see their applications.

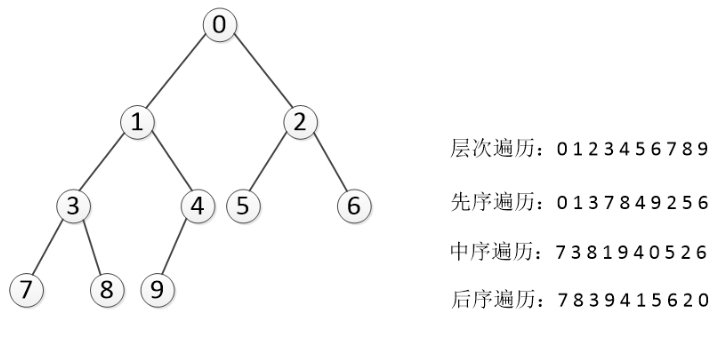
Preorder traversal

In preorder traversal, we first access the root node, then recursively use preorder traversal to access the left subtree, and then recursively use preorder traversal to access the right subtree
Root node - > left subtree - > right subtree

def preorder(self, node):
    """Recursive implementation of preorder traversal"""
    if node == None:
        return
    print(node.item)
    self.preorder(node.lchild)
    self.preorder(node.rchild)

Medium order traversal

In middle order traversal, we recursively use middle order traversal to access the left subtree, then access the root node, and finally recursively use middle order traversal to access the right subtree
Left subtree - > root node - > right subtree

def inorder(self, node):
    """Order traversal in recursive implementation"""
    if node == None:
        return
    self.inorder(node.lchild)
    print(node.item)
    self.inorder(node.rchild)

Postorder traversal in postorder traversal, we first recursively use postorder traversal to access the left subtree and right subtree, and finally access the root node
Left subtree - > right subtree - > root node

def postorder(self, node):
    """Recursive implementation of subsequent traversal"""
    if node == None:
        return
    self.postorder(node.lchild)
    self.postorder(node.rchild)
    print(node.item)

61. A binary tree is determined by traversal

A binary tree is determined by traversal

Subsequent traversal: about 7 8 3 9 4 1 5 6 20

Middle order traversal: 7 # 3 8 1 9 4 0 5 2 6 # left root right

1. The last bit of subsequent traversal is 0, indicating that the root is 0
2. Middle order traversal: 7 ＾ 3 8 1 9 4 ＾ 0 ＾ 5 2 6
3. Subsequent traversal: 7 8 3 9 4 1 # 5 6 2 # 0
4. 7 8 3 9 4 1 the last digit is 1, indicating that the root is 1
5. Middle order traversal: 7 3 8 # 1 # 9 4 # 0 # 5 2 6