1. Shortest path problem with conditional constraints

The shortest path problem is to find the shortest path between two vertices in graph theory. It is usually to find the shortest weighted path.

Conditional shortest path refers to the shortest path with constraints and restrictions. For example, vertex constraints, including restrictions on required or prohibited points; Side constraints, including mandatory or prohibited sections; It also includes the restriction of the length of the unauthorized path, that is, reaching the end point after several steps. Furthermore, there is the shortest path problem with double objective constraints, which is to find the route with the least cost in the shortest distance; The shortest path problem under traffic restrictions needs to consider the constraints of steering restriction and delay.

Generally speaking, solving the shortest path problem with constraints can be divided into two basic methods: one is based on the shortest path algorithm without constraints. Each effective path in the solution process is judged by constraints. If all constraints are met, continue, and if the constraints are not met, abandon the path; Another method is to transform the problem into a constrained programming problem based on the characteristics of specific problems and selection algorithms.

However, if NetworkX is used to solve the shortest path problem with constraints, there will be some difficulties in using these two methods. The reason is that the Dijkstra algorithm, Bellman Ford algorithm, Floyd algorithm and heuristic algorithm A * provided by NetworkX are encapsulated functions and do not provide options and interfaces for setting constraints. Therefore, users cannot add condition judgment statements into the programs of these encapsulated functions. This problem exists not only in the Network toolkit of Python language, but also in the toolkit of other computer languages: its own programming sequence is time-consuming and laborious, but it can be modified and extended as needed; It is very convenient to directly call the algorithm function of the toolkit, but it cannot be modified or extended.

However, NetworkX can generate all simple paths between two vertices and get a list of the edges of all simple paths. Using the simple path algorithm, the shortest path problem with vertex constraints and edge constraints can be solved by judging the constraints.

2. Problem case: optimal path analysis of ants

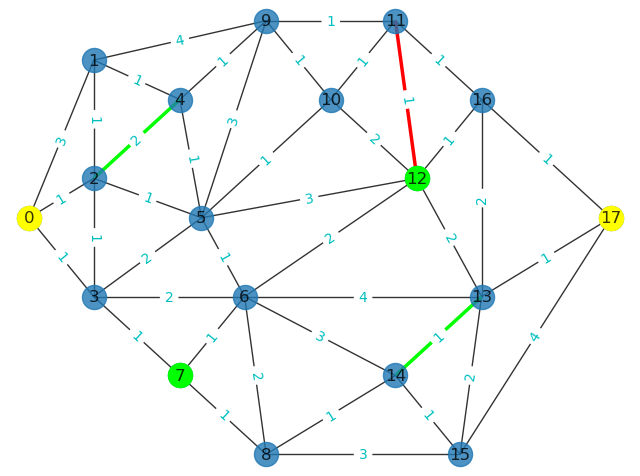
The ant nest has several storage rooms (indicated by the circle in the figure), and the storage rooms are connected by paths (the path topology is shown in the figure). The figure is undirected. The cost of path passing is shown in the figure on the line, and the cost of path passing in the positive and negative directions is the same. The optimal path from the starting point N0 to the ending point N17 is required, and the limiting conditions need to be met:

• It needs to reach the destination with the least cost as far as possible;
• Must pass through the green node in the figure;
• It must pass through two green sections in the figure;
• The red section in the figure must be avoided.

Note: this case is from the 12th mathematical modeling competition of Xi'an University of Posts and telecommunications. This paper is adapted.

Youcans original series( https://blog.csdn.net/youcans )

3. NetworkX solves the shortest path problem with conditional constraints

3.1 drawing creation and visualization

Python routines (NetworkX)

# networkX_E3.py
# Demo of shortest path with NetworkX
# Copyright 2021 YouCans, XUPT
# Crated: 2021-05-20

import matplotlib.pyplot as plt # Import Matplotlib Toolkit
import networkx as nx  # Import NetworkX Toolkit

# Question 1: optimal path analysis of ants (question B of the 12th mathematical modeling competition of Xi'an University of Posts and Telecommunications)

gAnt = nx.Graph()  # Create: empty undirected graph
gAnt.add_weighted_edges_from([(0,1,3),(0,2,1),(0,3,1),
                            (1,2,1),(1,4,1),(1,9,4),
                            (2,3,1),(2,4,2),(2,5,1),
                            (3,5,2),(3,6,2),(3,7,1),
                            (4,5,1),(4,9,1),
                            (5,6,1),(5,9,3),(5,10,1),(5,12,3),
                            (6,7,1),(6,8,2),(6,12,2),(6,13,4),(6,14,3),
                            (7,8,1),
                            (8,14,1),(8,15,3),
                            (9,10,1),(9,11,1),
                            (10,11,1),(10,12,2),
                            (11,12,1),(11,16,1),
                            (12,13,2),(12,16,1),
                            (13,14,1),(13,15,2),(13,16,2),(13,17,1),
                            (14,15,1),
                            (15,17,4),
                            (16,17,1)])  # Add multiple weighted edges to the graph: (node1,node2,weight)

pos={0:(1,8),1:(4,12),2:(4,9),3:(4,6),4:(8,11),5:(9,8),  # Specify vertex position
     6:(11,6),7:(8,4),8:(12,2),9:(12,13),10:(15,11),11:(18,13),
     12:(19,9),13:(22,6),14:(18,4),15:(21,2),16:(22,11),17:(28,8)}
nx.draw(gAnt, pos, with_labels=True, alpha=0.8)
labels = nx.get_edge_attributes(gAnt,'weight')
nx.draw_networkx_edge_labels(gAnt,pos,edge_labels=labels, font_color='c') # Display weight
nx.draw_networkx_nodes(gAnt,pos,nodelist=[0,17],node_color='yellow')  # Set vertex color
nx.draw_networkx_nodes(gAnt,pos,nodelist=[7,12],node_color='lime')  # Set vertex color
nx.draw_networkx_edges(gAnt,pos,edgelist=[(2,4),(13,14)],edge_color='lime',width=2.5)  # Sets the color of the edges
nx.draw_networkx_edges(gAnt,pos,edgelist=[(11,12)],edge_color='r',width=2.5)  # Sets the color of the edges
plt.show()

Operation results

This program draws the network diagram, including the weights of vertices, edges and edges, and the color settings of special vertices and edges.

Program description

1. Creation of diagram. This example uses NX Graph () creates an undirected graph, and then uses Gant add_ weighted_ edges_ The from () function adds multiple weighted edges to the graph in a list, and each weighted edge is represented by a tuple (node1,node2,weight).
2. Drawing of drawings. Use NX When drawing with draw(), the default node position is not ideal. You can use the POS attribute parameter to specify the node position. POS is the dictionary data type. Set the node location in the format of node:(x_pos,y_pos).
3. Displays the weight of the edge. Use NX draw_ networkx_ edge_ Labels () can draw the attributes of edges. In this example, select the display weight attribute.
4. Set vertex attributes. nx.draw_networkx_nodes() can set the attributes of vertices, such as setting the color attribute node for nodes in the nodelist list_ color.
5. Set the properties of the edge. nx.draw_networkx_edges() can set the properties of edges. For example, set the lineweight property width and color property edge for the edges in the edgelist list_ color.

3.2 unrestricted shortest path

Procedure description

1. For the shortest path problem without constraints, NetworkX provides functions of Dijkstra algorithm, Bellman Ford algorithm, Floyd algorithm and heuristic algorithm A *.
2. The routine uses NX dijkstra_ Path() and NX dijkstra_ path_ Length() calls Dijkstra algorithm to find the shortest weighted path and the shortest weighted path length between two specified vertices.

Python routines (NetworkX)

# The shortest weighted path between two specified vertices
minWPath1 = nx.dijkstra_path(gAnt, source=0, target=17)  # Shortest weighted path from vertex 0 to vertex 17
# The length of the shortest weighted path between two specified vertices
lMinWPath1 = nx.dijkstra_path_length(gAnt, source=0, target=17)  #Shortest weighted path length
print("\n Question 1: No restrictions")
print("S reach E Shortest weighted path: ", minWPath1)
print("S reach E Shortest weighted path length: ", lMinWPath1)

Operation results

Question 1: No restrictions
S reach E Shortest weighted path:  [0, 2, 5, 10, 11, 16, 17]
S reach E Shortest weighted path length:  6

3.3 restrictions: prohibited points or prohibited edges

Program description

1. The processing of prohibited points or prohibited edges is relatively simple. You can delete the corresponding prohibited vertices or prohibited edges from the graph. Of course, it's easier not to add these vertices and edges when creating a graph, but they can't be reflected when drawing.
2. Use remove_node(n) deletes the specified vertex n, remove_edge(u,v) deletes the specified edge (u,v).
3. Use remove_nodes_from([n1,... nk]) delete multiple vertices, remove_edges_from([(u1,v1),... (uk,vk)]) deletes multiple edges.
4. The points and edges deleted in the routine are inconsistent with the requirements in the case problem for the use of the example deletion function. The same below.

Python routine

# 2. Restrictions: prohibited points or prohibited edges
# Solution: remove forbidden vertices or edges from the graph
gAnt.remove_nodes_from([5])  # Delete vertices through vertex label 5
gAnt.remove_edge(13,17)  # Delete edges (13,17)
minWPath2 = nx.dijkstra_path(gAnt, source=0, target=17)  # Shortest weighted path from vertex 0 to vertex 17
lMinWPath2 = nx.dijkstra_path_length(gAnt, source=0, target=17)  #Shortest weighted path length
print("\n Question 2: Suppress point or edge constraints")
print("S reach E Shortest weighted path: ", minWPath2)
print("S reach E Shortest weighted path length: ", lMinWPath2)

Operation results

Question 2: Suppress point or edge constraints
S reach E Shortest weighted path:  [0, 3, 6, 12, 16, 17]
S reach E Shortest weighted path length:  7

3.4 limiting conditions: a necessary point

Program description

1. When the limiting condition is a necessary point, the original problem can be divided into two subproblems: subproblem 1 is from the starting point to the necessary point, and subproblem 2 is from the necessary point to the end point.
2. For the two subproblems, the shortest weighted path and the shortest weighted path length are calculated by Dijkstra algorithm respectively, and then combined to obtain the shortest weighted path and the shortest weighted path length of the original problem passing through the necessary points.

Python routine

# 3. Limiting conditions: a necessary point
# Solution: it is divided into two problems. Problem 1 is from the starting point N0 to the necessary point N6, and problem 2 is from the necessary point N6 to the end point N17
minWPath3a = nx.dijkstra_path(gAnt, source=0, target=6)  # Shortest weighted path from N0 to N6
lMinWPath3a = nx.dijkstra_path_length(gAnt, source=0, target=6)  # Shortest weighted path length
minWPath3b = nx.dijkstra_path(gAnt, source=6, target=17)  # Shortest weighted path from N6 to N17
lMinWPath3b = nx.dijkstra_path_length(gAnt, source=6, target=17)  # Shortest weighted path length
minWPath3a.extend(minWPath3b[1:]) # Splice minWPath3a and minWPath3b and remove N7
print("\n Question 3: Constraint of a necessary point")
print("S reach E Shortest weighted path: ", minWPath3a)
print("S reach E Shortest weighted path length: ", lMinWPath3a+lMinWPath3b)

Operation results

Question 3: Constraint of a necessary point
S reach E Shortest weighted path:  [0, 3, 6, 12, 16, 17]
S reach E Shortest weighted path length:  7

3.5 restrictions: multiple necessary points (scheme I)

Program description

1. When the restriction condition is two or more necessary crossing points, the order of the starting point, the ending point and each necessary crossing point is uncertain, that is, starting from the starting point, you don't know which necessary crossing point to go first, so it's not suitable to use the method of subsection to find the minimum path.
2. NetworkX provides all_ simple_ The paths() function can generate all simple paths between two vertices. Using the simple path algorithm, the shortest path problem with multiple vertex constraints can be solved by judging the constraints.
3. The steps of program implementation include: (1) traversing a simple path with a starting point of 0 and an ending point of 17; (2) Check whether the path meets the constraints including vertices N7 and N15; (3) Find the path with the shortest weighted length among the simple paths that meet the constraints; (4) Find the weighted path length of the shortest path.
4. This routine is very concise. It comprehensively uses the concise writing of several Python language loops and judgment structures, which needs to be analyzed step by step.

Python routine

# 4. Restrictions: multiple necessary points (N7,N15)
# Solution: traverse the simple path from the beginning to the end, and find the shortest path that meets the conditions of the necessary points
minWPath4 = min([path  # Returns the path with the minimum key
    for path in nx.all_simple_paths(gAnt, 0, 17)  # All simple paths with a starting point of 0 and an ending point of 17 in gAnt
    if all(n in path for n in (7, 15))], # Satisfy that the path includes vertices N7 and N15
    key=lambda x: sum(gAnt.edges[edge]['weight'] for edge in nx.utils.pairwise(x))) # key is the weighted path length
lenPath = sum(gAnt.edges[edge]['weight'] for edge in nx.utils.pairwise(minWPath4))  # Find the weighted path length of the specified path
print("\n Question 4: Constraints of multiple required points")
print("S reach E Shortest weighted path: ", minWPath4)
print("S reach E Shortest weighted path length: ", lenPath)

Operation results

Question 4: Constraints of multiple required points
S reach E Shortest weighted path:  [0, 3, 7, 8, 14, 15, 13, 17]
S reach E Shortest weighted path length:  8

3.6 restrictions: multiple necessary points (scheme II)

Program description

1. The problem in this example is actually the same as that in 3.5. The limiting conditions are multiple necessary vertices N7 and N15, and the solution is all_ simple_ The paths() function generates all simple paths between two vertices, and the steps of program implementation are similar.
2. This scheme is written according to the typical cycle and judgment structure, which is convenient for reading and understanding. In addition, if there are other constraints or subtasks that need to be processed in the loop, such a structure is easier to implement.

Python routine

# 5. Restrictions: multiple necessary points (N7,N15)
# Solution: traverse the simple path from the beginning to the end, and find the shortest path that meets the conditions of the necessary points
lMinWPath5 = minWPath5 = 1e9
for path in nx.all_simple_paths(gAnt, 0, 17):
    if all(n in path for n in (7,15)):  # Satisfy that the path includes vertices N7 and N15
        lenPath = sum(gAnt.edges[edge]['weight'] for edge in nx.utils.pairwise(path))
        if lenPath < lMinWPath5:
            lMinWPath5 = lenPath
            minWPath5 = path
print("\n Question 5: Constraints of multiple required points")
print("S reach E Shortest weighted path: ", minWPath5)
print("S reach E Shortest weighted path length: ", lMinWPath5)

Operation results

Question 5: Constraints of multiple required points
S reach E Shortest weighted path:  [0, 3, 7, 8, 14, 15, 13, 17]
S reach E Shortest weighted path length:  8

3.7 limiting conditions: required edge

Program description

1. The idea is to combine the implementation process of Dijkstra algorithm and take the limiting condition as the condition to reduce the search space, which can reduce the complexity of the algorithm. However, for multiple necessary edges, it is difficult to improve the basic unconstrained algorithm. The usual processing method is to add a process to judge whether the constraints are met.
2. This example still continues the idea of dealing with multiple mandatory points. Using the simple path algorithm, the shortest path problem with multiple mandatory edge constraints can be solved by judging the constraints, and the mandatory point constraints can be dealt with at the same time.
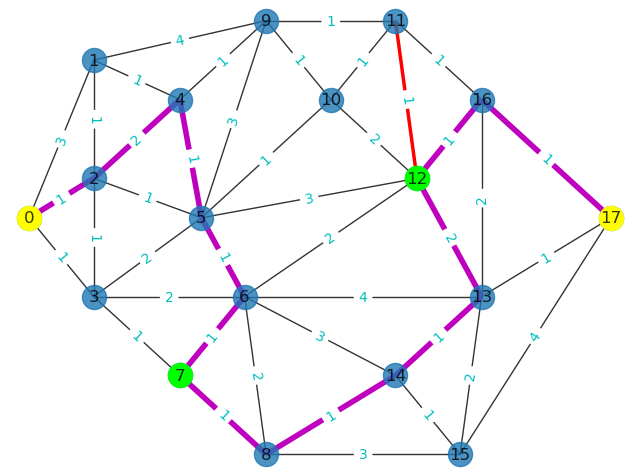
3. This routine corresponds to various constraints in the case: it must pass through the green node in the figure; It must pass through two green sections in the figure; The red section in the figure must be avoided; Reach the destination with the least cost possible.
4. The framework and steps of this routine are the same as those in 3.6. This is a general framework for traversing simple paths and judging constraints.
5. The role of all(n in path for n in (2,4,7,12,13,14)) is to judge whether the path includes necessary points N7 and N12; Second, judge whether the path includes the vertices of the necessary edges (2,4), (13,14), which can not only reduce the amount of calculation, but also ensure that there will be no error when using index() to find the vertex position.

Python routine

# 6. Limiting conditions: necessary edges (N2,N4), (N13,N14), necessary points N7,N12
# Solution: traverse the simple path from the beginning to the end, and find the shortest path that meets the necessary edge conditions
gAnt.remove_edge(11,12)  # Forbidden edge (11,12)
lMinWPath6 = minWPath6 = 1e9  # Set initial value
for path in nx.all_simple_paths(gAnt, 0, 17):  # All simple paths with a start point of 0 and an end point of 17
    if all(n in path for n in (2,4,7,12,13,14)): # Satisfy that the path includes vertices N7 and N12
        # Check (N2,N4)
        p1 = path.index(2)  # Position of N2
        if (path[p1-1]!=4 and path[p1+1]!=4): continue  # Judge whether N2~N4 are adjacent
        # Check (N13,N14)
        p2 = path.index(13)  # # Location of N13
        if (path[p2-1]!=14 and path[p2+1]!=14): continue  # Judge whether N13~N14 are adjacent
        lenPath = sum(gAnt.edges[edge]['weight'] for edge in nx.utils.pairwise(path))
        if lenPath < lMinWPath6:
            lMinWPath6 = lenPath
            minWPath6 = path

print("\n Question 6: Constraints of multiple necessary edges and points")
print("S reach E Shortest weighted path: ", minWPath6)
print("S reach E Shortest weighted path length: ", lMinWPath6)

edgeList = []
for i in range(len(minWPath6)-1):
    edgeList.append((minWPath6[i],minWPath6[i+1]))
nx.draw_networkx_edges(gAnt,pos,edgelist=edgeList,edge_color='m',width=4)  # Sets the color of the edges
plt.show()  # YouCans, XUPT

Operation results

Question 6: Constraints of multiple necessary edges and points
S reach E Shortest weighted path:  [0, 2, 4, 5, 6, 7, 8, 14, 13, 12, 16, 17]
S reach E Shortest weighted path length:  13

Follow the original series of Youcans( https://blog.csdn.net/youcans )

• Python digital analog notes - operation of NetworkX (1) diagram
  https://blog.csdn.net/youcans/article/details/116942703
• Network2 shortest path
  https://blog.csdn.net/youcans/article/details/116999881

Copyright description:

The content and routines of this article are original by the author and are not reprinted from books or online content.
The case questions in this article come from:

For original works of YouCans, if reprinted, the original link shall be marked.
Copyright 2021 YouCans, XUPT
Crated: 2021-05-20