sort

Quick row

arr = [np.random.randint(1,100) for i in range(11)]
def quickSort(data):
    if len(data)<2:
        return data
    else:
        tmp = data[-1]
        data.pop()
        left,right = [],[]
        for item in data:
            if item <=tmp:
                left.append(item)
            else:
                right.append(item)
        return quickSort(left)+[tmp]+quickSort(right)
print(quickSort(arr))

Merge sort

def mergeSort(data):
    if len(data)<=1:
        return data
    else:
        idx = int(len(data)/2)
        left = mergeSort(data[:idx])
        right = mergeSort(data[idx:])
        return merge(left,right)
def merge(left,right):
    ans = []
    while left and right:
        if left[0]<right[0]:
            ans.append(left[0])
            left.pop(0)
        else:
            ans.append(right[0])
            right.pop(0)
    ans += left
    ans += right
    return ans

arr = [np.random.randint(1,100) for i in range(11)]
print(arr)
print(mergeSort(arr))

All incremental subsequences

Use recursive thinking to solve

def findallis(nums):
	res = []
	track = []
	
	def dfs(numd):
	    if not numd:
	        return
	    if not track or (numd[0] >= track[-1]):
	        track.append(numd[0])
	        if len(track) >= 2 and track not in res:
	            res.append(track[:])
	        dfs(numd[1:])
	        track.pop()
	    dfs(numd[1:])
	dfs(nums)
	return res

Length of the longest increasing subsequence

This problem is different from the longest continuous increasing subsequence. The continuous increasing sequence can be solved in the form of traversal

# N*N complexity based on dynamic programming
def longestIncreseq(arr)
	n = len(arr)
	dp = [1]*n
	for i in range(n):
		for j in range(i):
			if arr[j]<arr[i]:
				dp[i] = max(dp[i],dp[j]+1)
	return max(dp)

# Based on the greedy dichotomy, if you want to have the longest increasing subsequence, it means to rise at the slowest speed.
#During the loop, if there is an element larger than the last element of the current sequence, it will be added,
#If it is smaller than the last one, the binary finds a specific location and replaces it.
#This may violate the requirements of subsequence, but the length is correct due to substitution
def longestIncreseq(arr)
	n = len(arr)
	d = []
	for item in arr:
		if not d or item>d[-1]:
			d.append(item)
		else:
			l,r = 0,len(d)-1
			loc = r
			mid = (l+r)//2
			while l<=r:
				if d[mid]>=item:
					loc = mid
					r = mid-1
				else:
					l = mid+1
			d[loc]=item
	return len(d)

Rebuild binary tree

The binary tree is reconstructed according to the preorder and inorder traversal results

# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        def myBuildTree(preorder_left: int, preorder_right: int, inorder_left: int, inorder_right: int):
            if preorder_left > preorder_right:
                return None
            
            # The first node in the preorder traversal is the root node
            preorder_root = preorder_left
            # Locate the root node in the middle order traversal
            inorder_root = index[preorder[preorder_root]]
            
            # First establish the root node
            root = TreeNode(preorder[preorder_root])
            # Get the number of nodes in the left subtree
            size_left_subtree = inorder_root - inorder_left
            # The left subtree is constructed recursively and connected to the root node
            # The elements "size_left_subtree starting from the left boundary + 1" in the preorder traversal correspond to the elements "from the left boundary to the root node location - 1" in the inorder traversal
            root.left = myBuildTree(preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1)
            # The right subtree is constructed recursively and connected to the root node
            # The element "starting from the left boundary + 1 + number of left subtree nodes to the right boundary" in the preorder traversal corresponds to the element "locating from the root node + 1 to the right boundary" in the inorder traversal
            root.right = myBuildTree(preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right)
            return root
        
        n = len(preorder)
        # Construct hash mapping to help us quickly locate the root node
        index = {element: i for i, element in enumerate(inorder)}
        return myBuildTree(0, n - 1, 0, n - 1)

Symmetric binary tree

def func(root):
    def recur(r1,r2):
        if not r1 and not r2:
            return True
        elif not r1 or not r2 or r1.val!=r2.val:
            return False
        return recur(r1.left,r2.right) and recur(r1.right,r2.left)
    if root:
        recur(root.left,root.right)
    else:
        return True

Binary tree image

#Define data structure
class TreeNode:
	def __init__(self,x):
	self.val = x
	self.left = None
	self.right = None
	
def mirrortree(root):
	if not root:
		return
	else:
		tmp = root.left
		root.left = root.right
		root.right = tmp
		mirrorTree(root.left)
		mirrorTree(root.right)
	return root

Same tree

def isSametree(p,q):
	if not p and not q:
		return True
	elif not p or not q: #The last judgment condition and the condition of this line cannot exchange positions, because when P and Q are empty at the same time, they also meet any condition that is empty, that is, the first condition is a special case of the second condition. Therefore, it is necessary to judge the special case first, and the exchange order will have a logical problem
		return False
	elif p.val!=q.val:
		return False
	else:
		return isSametree(p.left,q.left) and isSametree(p.right,q.right)

Full arrangement

def permute(self, nums: List[int]) -> List[List[int]]:
    res = []
    path = []
    def dfs(arr):
        if not arr:
            res.append(path[:])
        for i in range(len(arr)):
            path.append(arr[i])
            dfs(arr[0:i]+arr[(i+1):])
            path.pop()
    dfs(nums)
    return res

Circularly incrementing the binary in the array to find a target

Binary search based on recursion

arr = [4,5,6,7,9,10,12,123,-2,1,2,3]
target = -2

def find_target(start,end):
    mid = int((start+end)/2)
    if arr[mid]==target:
        return mid
    elif start==end and arr[mid]!=target:
        return -1
    elif arr[mid]>arr[start] and target<arr[start] or target>arr[mid]:
        return find_target(mid+1,end)
    elif arr[mid]>arr[start] and target>=arr[start] and target<=arr[mid]:
        return find_target(start,mid-1)
    elif arr[mid]<arr[start] and target<=arr[end] and target>=arr[mid]:
        return find_target(mid+1,end)
    elif arr[mid]<arr[start] and target>arr[end] or target<arr[mid]:
        return find_target(start,mid-1)
print(find_target(0,len(arr)-1))

Non recursive binary search

arr = [4,5,6,7,9,10,12,123,-2,1,2,3]
target = 12

def find_target(arr):
    l,r = 0,len(arr)-1
    while l<=r:
        mid = int((l+r)/2)
        # print(mid)
        if arr[mid]==target:
            return mid
        else:
            if arr[mid]>=arr[l]:
                if arr[l]<=target<arr[mid]:
                    r = mid-1
                else:
                    l=mid+1
            else:
                if arr[r]>=target>arr[mid]:
                    l = mid+1
                else:
                    r=mid-1
    return -1
print(find_target(arr))

Non recursive traversal tree

Recursive traversal tree

def threeOrders(root):
    # write code here
    def preorder(root):
        if root.left is None and root.right is None:
            return [root.val]
        return [root.val] + preorder(root.left) + preorder(root.right)

    def midorder(root):
        if root.left is None and root.right is None:
            return [root.val]
        return midorder(root.left) + [root.val] + midorder(root.right)

    def postorder(root):
        if root.left is None and root.right is None:
            return [root.val]
        return postorder(root.left) + postorder(root.right) + [root.val]

    return [preorder(root), midorder(root), postorder(root)]

Preorder traversal

def preorder(root):
	if not root:
		return []
	res = []
	stack = [root]
	while stack:
		root = stack.pop()
		res.append(root.val)
		if root.right:
			stack.append(root.right)
		if root.left:
			stack.append(root.left) 
	return res

Postorder traversal

The preorder traversal is about the root, and the postorder is about the root. Change the left and right in the preorder traversal to right and left, that is, the root is right and left, and finally reverse the order to become left and right roots

def postorder(root):
	if not root:
		return []
	res = []
	stack = [root]
	while stack:
		node = stack.pop()
		res.append(node.val)
		if root.left:
			stack.append(root.left)
		if root.right:
			stack.append(root.right)
	return res[::-1] 

Medium order traversal

def inorder(root):
	if not root:
		return []
	res = []
	stack = []
	cur = root
	while cur or stack:
		if cur:
			stack.append(cur) #append is before, which causes cur to be a valid leaf node for the last time
			cur = cur.left
		else:
			cur = stack.pop()
			res.append(cur.val)
			cur = cur.right  #The right subtree of the first leaf node is empty, so the next cycle will directly pop again to get the root node of the first leaf node,
	return res

Binary tree sequence traversal

Traverse layer by layer and output once

def cengxubianli(root):
    nodes = [root]
    res = []
    while nodes:
        node = nodes[0]
        nodes.pop(0)
        res.append(node.val)
        if node.left:
            nodes.append(node.left)
        if node.right:
            nodes.append(node.right)
    return res

Layer by layer traversal and layer by layer output

def levelOrder(root):
    nodes = [root]
    res = []
    while nodes:
        layer = nodes
        tmp_res = []
        tmp_nodes = []
        for node in layer:
            tmp_res.append(node.val)
            if node.left:
                tmp_nodes.append(node.left)
            if node.right:
                tmp_nodes.append(node.right)
        nodes = tmp_nodes
        res.append(tmp_res)
    return res

The binary tree traverses all paths

Rainwater connection

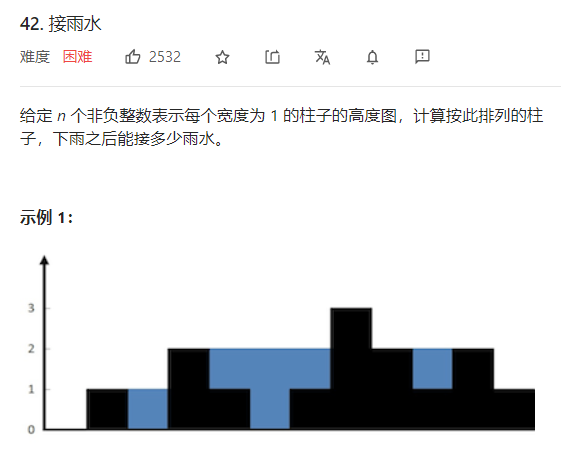
def func(heights):
	n = len(heights)
	if n==0:
		return 0
	res = []
	leftmax = [heights[0]]+[0]*(n-1) #This array represents the highest value to the left of each position i
	rightmax = [0]*(n-1)+[heights[-1]] #This array represents the highest value to the right of each position i
	#Traverse twice to determine the above two arrays
	for i in range(1,n):
		leftmax[i] = max(leftmax[i-1],heights[i])
	for i in range(n-2,-1,-1):
		rightmax[i] = max(rightmax[i+1],heights[i])
	#Cycle to calculate the amount of rainwater that can be connected at each position: the lower value of the highest value on the left and right sides determines the upper limit of water level, and the heights[i] determines where the bottom is
	for i in range(n):
		current_vol = min(leftmax[i],rightmax[i])-heights[i]
		res.append(current_vol)
	return sum(res)

Area of the largest square 1 matrix

leetcode221 inputs the 01 matrix of n*m and outputs the area of the largest square 1 matrix

def maximalSquare(matrix: List[List[str]]) -> int:
    rows,cols = len(matrix),len(matrix[0])
    if rows==0 or cols ==0:
        return 0
    maxside = 0
    dp = [[0]*cols for _ in range(rows)]

    for i in range(rows):
        for j in range(cols):
            if matrix[i][j]=="1":
                if i==0 or j==0: #It is equivalent to initialization. The first row and the first column are processed
                    dp[i][j]=1
                else:
                    dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1 #This calculation can limit the matrix to always meet the square requirements
            maxside = max(dp[i][j],maxside)
    return maxside*maxside

Linked list

Reverse linked list

def reverse(head):
	prev = None
	cur = head
	while cur:
		nex = cur.next
		cur.next = prev
		prev = current
		current = next
	return prev

A group of K inverted linked lists

def reverseK(head,k):
	def reverse(head,tail):
		#The tool function is used to flip a group of linked lists and return the head and tail nodes, which is used to splice the linked lists at the back
		pre = None
		tail = head
		while head:
			nex = head.next
			head.next = pre
			pre = head
			head = nex
		return pre,tail
	res = Listnode(0) #Define a new linked list to store the results
	ans = res
	lessthanK = False:
	while head:
		cur_head = head
		for i in range(k-1):
			if head.next:
				head = head.next
			else:
				lessthanK = True
		if lessthanK:
			return ans.next
		else:
			cur_tail = head
			head = head.next
			cur_tail.next = None #Cut off the linked list
			reverse_head,reverse_tail = reverse(cur_head,cur_tail) #Turn over the rotor list
			
			res.next = reverse_head #Connect the header of the inverted sub chain to the tail of the result
			reverse_tail.next = head #Connect the remaining list to the tail of the reverse rotor list
			res = reverse_tail # Move the pointer to the end of the anti rotor list to prepare for the next cycle
	return ans.next

search

Maximum island area

def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
   	def dfs(i,j):
       	if i<0 or j<0 or i == len(grid) or j == len(grid[0]) or grid[i][j]==0:
			return 0
		grid[i][j]=0
		return 1+dfs(i,j+1)+dfs(i+1,j)+dfs(i,j-1)+dfs(i-1,j)

	row,col = len(grid),len(grid[0])
	ans = 0
	for i in range(row):
	    for j in range(col):
	        if grid[i][j]==1:
	            area = dfs(i,j)
	            ans = max(area,ans)
	return ans

Number of islands

def numIslands(grid) :
    visited = [[0] * len(grid[0]) for _ in range(len(grid))]
    def dfs(i, j):
        if i < 0 or i > len(grid) - 1 or j < 0 or j > len(grid[0]) - 1 or grid[i][j] == "0" or visited[i][j] == 1:
            return

        visited[i][j] = 1
        dfs(i - 1, j)
        dfs(i + 1, j)
        dfs(i, j - 1)
        dfs(i, j + 1)

    count = 0
    for i in range(len(grid)):
        for j in range(len(grid[0])):
            if grid[i][j] == "1" and visited[i][j] == 0:
                count += 1
                dfs(i, j)
    return count

Longest palindrome string

Dynamic programming solution

def longesthuiwenchuan(s):
	n = len(s)
	if n<2:
		return s
	max_len = 1
	start = 1
	dp = [[False]*n for _ in range(n)] #dp[i][j] indicates whether s[i...j] is a palindrome string
	#initialization
	for i in range(n):
		dp[i][i] = True
		if i+1<n:
			dp[i][i+1] = (s[i]==s[i+1])
	# Circularly calculate each position because dp[i][j] = dp[i+1][j-1] and (s[i]==s[i+1]),
	# That is, the upper right point is determined by the value of the lower left point, so the cycle order is that the outer ring is a column and the inner ring is a row
	for j in range(2,n):
		for i in range(j-1):
			dp[i][j] = dp[i+1][j-1] and (s[i]==s[j])
	# Traverse the entire dp table to determine the starting point of the longest palindrome string
	for i in range(n):
		for j in range(i,n):
			if j-i+1>max_len:
				max_len = j-i+1
				start = i
	return s[start:start+max_len]

Central diffusion method

Traverse each point, spread from the middle to both sides, and judge whether it meets the palindrome string requirements one by one

class Solution:
    def __init__(self):
        self.res = []
        self.max_len = 0
    def judge(self,start,end,s):
        while start>=0 and end<len(s):
            if s[start]==s[end]:
                start-=1
                end+=1
            else:
                break
        self.res = s[start+1:end]

    def longestPalindrome(self, s: str) -> str:
        length = len(s)
        if length == 1:
            return s
        ans = []
        for i in range(length-1):
            self.judge(i,i,s)
            if self.max_len<len(self.res):
                ans = self.res
                self.max_len = len(self.res)
            
            self.judge(i,i+1,s)
            if self.max_len<len(self.res):
                ans = self.res
                self.max_len = len(self.res)
        return ans

Edit distance

def editDistance(word1,word2):
    l1,l2 = len(word1),len(word2)
    if l1==0 or l2==0:
        return max(l1,l2)
	#Two empty characters are introduced in front of two strings to avoid initialization
	#An error caused by encountering the same character twice
    dp = [[i+j for j in range(l2+1)] for i in range(l1+1)] 

    for i in range(1,l1+1):
        for j in range(1,l2+1):
            if word1[i]==word2[j]:
                dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j] + 1, dp[i][j - 1] + 1)
            else:
                dp[i][j] = min(dp[i - 1][j - 1]+1, dp[i - 1][j] + 1, dp[i][j - 1] + 1)
    return dp[-1][-1]

Given a string array, a = ['ab', 'dbc', 'efg'], with a length of n, randomly select one character from each of the n strings each time to form a string with a length of n, and output all possible strings.

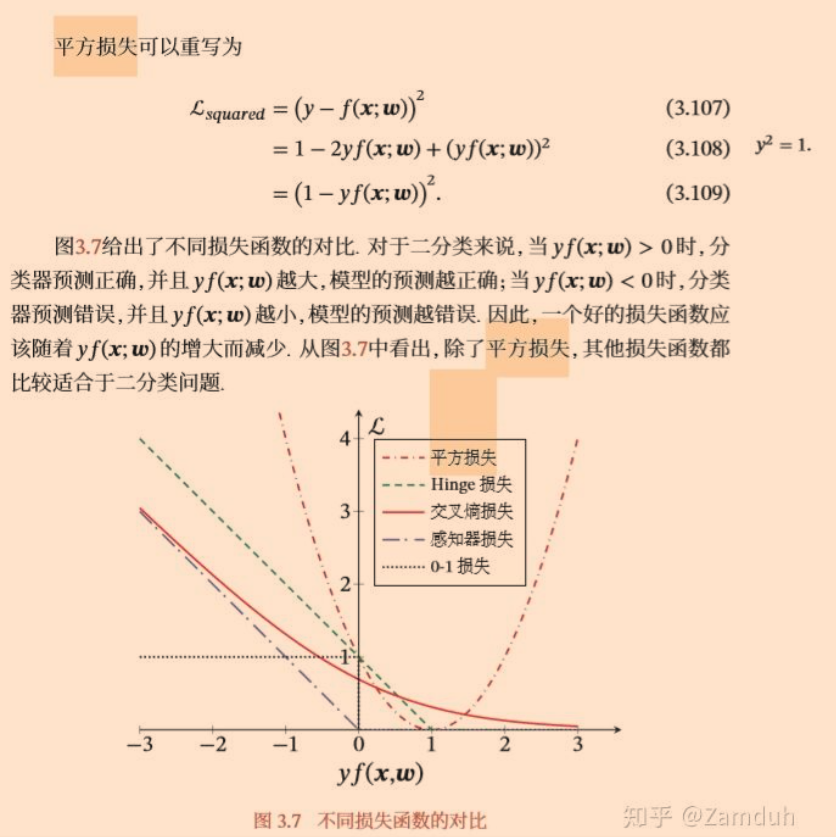
attention The mechanism can be regarded as three stages,
1. Calculate target output Q Key values associated with input features K Similarity of
2. The similarity is analyzed SoftMax Calculate normalization to weight
3. Values for all input characteristics V And weights 

self-attention In the mechanism, only attention The output in is replaced by the input, and the similarity between the input data is calculated

HR interview questions:

1. Self introduction highlights educational background, skill background and project experience
2. What are your strengths and weaknesses? Advantages: learning ability, problem abstract modeling ability, communication and execution ability
3. Why should we hire you?
4. Why choose our company?
5. What is career planning?
6. Do you accept overtime?
7. What else do you like to do besides work?
8. What is the longest thing to stick to or the most impressive thing?
9. Talk about an experience of your failure
10. What is the expected salary or rank?
11. Rhetorical question