Common sorting algorithms
- Algorithm: a calculation process and a method to solve the problem
- Program = data structure + algorithm
1, Basic concepts of algorithm
1. Time complexity
How to reflect the speed of the algorithm?
The time complexity is expressed by the number of runs

Example:
'''
No one answers the problems encountered in learning? Xiaobian created a Python exchange of learning QQ Group: 531509025
Look for like-minded friends to help each other,There are also good videos and tutorials in the group PDF e-book!
'''
print("hello world")
print("hello python")
print("hello algorithm")
#Above time complexity O(1)
for i in range(n):
print("hello world")
for j in range(n):
print("hello world")
#Time complexity O(n**2)
while n>1:
print(n)
n = n//2
The time complexity is recorded as O(log 2 n) or O(log n)
When the algorithm process is cyclically halved, log n will appear in the complexity formula
Summary of time complexity
Time complexity is a formula (unit) used to calculate the running time of an algorithm Generally speaking, algorithms with high time complexity are slower than those with low complexity. Time complexity of creation(Sort by efficiency) O(1) < O(logn) < O(nlogn) < O(n2) < O(n2 log n) < O(n3) Time complexity of complex problems O(n!) O(2**n) O(n**n)
How to judge the complexity of algorithm simply and quickly
Quickly judge the complexity of the algorithm, which is suitable for most simple cases Determine the size of the problem n Cycle halving process---> log n k Layer about n Cycle of --->n**k Complex situation: execute judgment according to the algorithm
2. Space complexity
Space complexity: an expression used to evaluate the memory footprint of an algorithm
The representation of spatial complexity is exactly the same as that of time complexity
- The algorithm uses several variables: O(1)
- The algorithm uses a one-dimensional list with length n: O(n)
- The algorithm uses a two-dimensional list of m rows and n columns: O(mn)
Space for time
3. Recursion
There are two conditions for recursion:
- Call itself
- End condition
4. Tower of Hanoi
Move n-1 disks from a through c to b
Move the n th disc from a to c
Move n-1 plates from b through a to c
n = 2
n = 3
def hanoi(n,a,b,c):
"""
n:express n A plate
a:a column
b:b column
c:c column
"""
if n>0:
hanoi(n-1,a,c,b)#Move n-1 plates from a through c to b
print('moving from %s to %s'%(a,c))
hanoi(n-1,b,a,c)#Move n-1 plates from b through a to c
- Recurrence formula of the number of movements of Hanoi Tower: h(x) = h(x-1) + 1 + h(x-1)
- h(64) = 18446744073709551615
2, Algorithm 8 sorting and searching algorithms
1. Sequential search
In some data elements, the process of finding the same data elements as a given keyword through certain methods
List lookup (linear table lookup): finds the specified element from the list
- Input: list, elements to be found
- Output: element subscript (normally returns None or - 1 when no element is found)
Built in list lookup function: index()
Sequential search: also called linear search, search sequentially from the first element of the list until the element is found or the last element of the list is searched
def linear_search(li,val): for ind,v in enumerate(li): if v == val: return ind else: return None #Time complexity: O(n)
2. Binary search
Binary search: also called split search. Starting from the initial candidate area li[0:n] with sequence table, the waiting area can be reduced by half by comparing the value to be searched with the middle value of the back selection. (precondition sort)
Use binary search in order. Sort first and then binary search in disorder. The time complexity will be greater than that of sequential search. If you often search in the future, you can sort, so that it will be easier to find in the future.
''' No one answers the problems encountered in learning? Xiaobian created a Python exchange of learning QQ Group: 531509025 Look for like-minded friends to help each other,There are also good videos and tutorials in the group PDF e-book! ''' from cal_time import * #Calculation function execution time module @cal_time def binary_search(li,val): """ li:list val:Find value for """ left = 0#List initial value position right = len(li) - 1#List end location while left <= right:#Candidate area has value mid = (left + right)//2 if li[mid] == val:#Found value, return index return mid elif li[mid] > val:#The value to be found is to the left of mid right = mid -1 else:#Li [mid] < Val on the right side of the value to be found left = mid + 1 else:#Can't find return None li = [1,2,3,4,5,6,7,8] binary_search(li,3) #Time complexity: #When the loop is halved, log n will appear in the complexity formula
3, Sort
1. List sorting
Sort: adjusts a group of "unordered" record sequences to "ordered" record sequence numbers
List sorting: change an unordered list into a sequential table
- Input: List
- Output: ordered lists
Ascending and descending
Built in sorting function: sort()
Common sorting algorithms
Bubble sorting Select sort Insert sort Quick sort Heap sort Merge sort Shell Sort Count sort Cardinality sort
2. Bubble sort
- Every two adjacent numbers in the list. If the front is larger than the back, exchange these two numbers
- After a sequence is completed, the unordered area decreases by one number and the ordered area increases by one number
- Code key point: range of times / unordered area.
- Time complexity: O(n**2)
''' No one answers the problems encountered in learning? Xiaobian created a Python exchange of learning QQ Group: 531509025 Look for like-minded friends to help each other,There are also good videos and tutorials in the group PDF e-book! ''' def bubble_sort(li): for i in range(len(li)-1):#Trip i for j in range(len(i)-i-1): if li[j] > li[j+1]: li[j],li[j+1] = li[j+1],li[j] print(li) li = [1,5,2,3,6] bubble_sort(li)
Bubble sort upgrade:
If there is no exchange during the trip, it can be considered that the order has been arranged and there is no need to arrange it later
def bubble_sort(li): for i in range(len(li)-1):#Trip i exchange = False for j in range(len(i)-i-1): if li[j] > li[j+1]: li[j],li[j+1] = li[j+1],li[j] exchange = True print(li) if not exchange: return
3. Select sort
- The minimum number of records to be sorted in a row is placed in the first position
- Once again, sort the smallest number in the unordered area of the record list and put it in the second position
- Sorting is not recommended
- Key points of the algorithm: ordered area and disordered area. The position of the smallest number of disordered areas
def select_sort_simple(li): new_li = [] for i in range(len(li)): min_val = min(li) li_new.append(min_val) li.remove(min_val) return li_new li = [3,2,5,10,9,2] print(select_sort_simple(li)) #This method is not recommended because a list is created #The complexity of min method is O(n), and the complexity of remove method is O(n)
Better selection sorting (in place sorting)
def select_sort(li): for i in range(len(li)-1):#i what's the first time min_location = i for j in range(i+1,len(li)): if li[j] < li[min_location]: min_location = j li[i],li[min_location] = li[min_location],li[i] print(li) li = [3,2,5,10,9,2] select_sort(li) Time complexity:O(n**2)
4. Insert sort
At the beginning, there is only one card in your hand (ordered area)
Touch one card at a time (from the disordered area) and insert it into the correct position of the existing card in your hand
''' No one answers the problems encountered in learning? Xiaobian created a Python exchange of learning QQ Group: 531509025 Look for like-minded friends to help each other,There are also good videos and tutorials in the group PDF e-book! ''' def insert_sort(li): for i in range(1,len(li)): #i indicates the subscript of the card touched temp = li[i] j = i - 1#j refers to the subscript of the card in hand while j>=0 and li[j] > temp: li[j+1] = li[j] j -= 1 li[j+1] = temp li = [3,2,5,10,9,2] print(insert_sort(li)) #Time complexity: O(n**2)
4. Quick sort
Quick sort idea:
Take an element p and make the element p return to the position. The list is divided into two parts by p. the left is smaller than p and the right is larger than p. the loop recursion is completed.
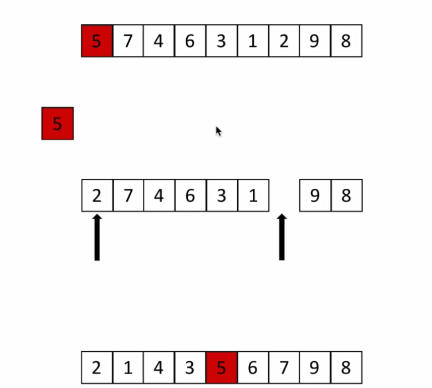
def partition(li,left,right):
temp = li[left] #Take out a value
while left<right:
while left <right and li[right] >=temp:#Find a number smaller than temp from the right
right-=1#Take a step to the left
li[left] = li[right]#Write the value on the right to the space on the left
print(li)
while left <right and li[left] <= temp:#Find a number larger than temp from the left
left += 1
li[right] = li[left]
li[left] = temp#Reset the extracted value
return left
#partition function: take out the first number temp, and put the numbers less than temp to the left of temp, and the numbers greater than temp to the right of temp.
def quick_sort(li,left,right):
if left<right:#At least 2 elements
mid = partition(li,left,right)
quick_sort(li,left,mid-1)
quick_sort(li,mid+1,right)
li = [5,7,4,6,3,1,2,9,9]
quick_sort(li,0,len(li)-1)
print(li)