Preface

The principle of the Huffman tree and its python implementation:
Q's knowledge blind spot in the recent interview, only remember the noun does not know its meaning. After three years of work, what you learned during the entrance examination for postgraduate studies is basically returned to the teacher. In addition to the list work may be used more, tree diagram related may basically remember only the noun.

I've read a lot of explanations on the Internet, but I still have to look for "Little Grey Brother" in this area of arithmetic. Let's go!!!

1. What is a Hafman tree?

Simply put, solve= W P L m i n = ∑ i = 1 n = l i s t . l e n g t h w e i g h t ( i ) ∗ p l ( i ) ， belt power road path long degree most Small Of two fork tree WPL_{min}= \sum_{i=1}^{n=list.length} {weight(i)} {*pl(i)} {, binary tree with minimum weighted path length} WPLmin =i=1_n=list.length weight(i) pl(i), an explanation of the basic principle of binary trees with minimal weighted path length can be seen Extra Detailed Analysis of Little Grey Brother.
WPL: Weighted Path Length of Tree

2. Drawing Hafman Trees on Principles

1. Build tree structure

_Here is the code translated directly according to the principle, which is a bit rigid, but it should be better understood. A pioneer built a haffmanClass to handle it, and I also did it. I think that's better than that here or to keep this, first impression:

def create(data : list, idx=0):
    if idx >= len(data):
        return None
    data.sort()#Sort Temporary Table
    #curAll = Node(None)
    curDic = {}#Store temporary Book tree structure
    for i in range(len(data)-1):
        data.sort()#Sort Temporary List
        cur = Node(data[0]+data[1])
        if i ==0:
            cur.left = Node(data[0])
            cur.right = Node(data[1])
            curDic[cur.name] = cur
        elif data[0] in curDic and data[1] in curDic:
            cur.left = curDic[data[0]]
            cur.right = curDic[data[1]]
            curDic[cur.name] = cur
            curDic.pop(data[0])
            curDic.pop(data[1])
        elif data[0] in curDic :
            cur.left = curDic[data[0]]
            cur.right = Node(data[1])
            curDic[cur.name] = cur
            curDic.pop(data[0])
        elif data[1] in curDic:
            cur.left = Node(data[0])
            cur.right = curDic[data[1]]
            curDic[cur.name] = cur
            curDic.pop(data[1])
        else:
            cur.left = Node(data[0])
            cur.right = Node(data[1])
            curDic[cur.name] = cur
        data.append(data[0]+data[1])
        data.pop(0)
        data.pop(0)

2. Visual Tree Structure

_is just a tree structure, but it is not easy to understand. So we use networkx to visualize the tree structure, to determine whether the output of nodes is correct, to understand the tree structure, this method can also be used for other trees:

def draw(node,data):   # Draw a node as root
    saw = defaultdict(int)

    def create_graph(G, node, p_name ="initvalue", pos={}, x=0, y=0, layer=1):
        if not node:
            return
        name = str(node.name)
        print("node.name:",name,"x,y:(",x,",",y,")l_layer:",layer)
        saw[name] += 1
        if name in saw.keys():
            name += ' ' * saw[name]
        if p_name != "initvalue" :
            G.add_edge(p_name, name)
        pos[name] = (x, y)

        l_x, l_y = x - 1 / (3 * layer), y - 1
        #print("l_x, l_y:",l_x, l_y)
        l_layer = layer + 1
        #print("l_layer:",l_layer)
        create_graph(G, node.left, name, x=l_x, y=l_y, pos=pos, layer=l_layer)

        r_x, r_y = x + 1 /( 3 * layer), y - 1
        #print("r_x, r_y:", r_x, r_y)
        r_layer = layer + 1
        create_graph(G, node.right,name, x=r_x, y=r_y, pos=pos, layer=r_layer)
        return (G, pos)

    graph = nx.DiGraph()
    graph.name
    graph, pos = create_graph(graph, node)
    #pos["     "] = (0, 0)
    print("pos:",pos)
    fig, ax = plt.subplots(figsize=(8, 10))  # Scale can be adjusted appropriately according to the depth of the tree
    color_map = []
    # for j,node in enumerate(graph.nodes):
    #Color Add Marker Leaf Node
    for degree in graph.out_degree:
        if int(degree[0]) in data and degree[1] == 0 :
            color_map.append('blue')
        else:
            color_map.append('green')
    #nx.draw(G, node_color=color_map, with_labels=True)
    nx.draw_networkx(graph, pos, ax=ax, node_size=1000,node_color=color_map)
    plt.show()

3. Hafman Encoding

_Of course it's about principle or direct search Little Grey Brother Arrangement
_My understanding of Huffman encoding is to maximize the space saved by characters (encoding) based on frequency of use.

def huffmanCode(tree,length):
    node = tree
    if not node:
        return
    elif not node.left and not node.right:
        x = str(node.name) + 'Coded as:'
        for i in range(length):
            x += str(b[i])
        dicDeepth[node.name] = x
        print(x)
        return
    b[length] = 0
    huffmanCode(node.left, length + 1)
    b[length] = 1
    huffmanCode(node.right, length + 1)

3. Complete Code

The code is as follows:

import networkx as nx
import matplotlib.pyplot as plt
from collections import defaultdict
import copy

dicDeepth = {}
b = list(range(10))

class Node:
    def __init__(self, val):
        self.name = val
        self.left = None
        self.right = None


def create(data : list, idx=0):
    if idx >= len(data):
        return None
    data.sort()
    #curAll = Node(None)
    curDic = {}
    for i in range(len(data)-1):
        data.sort()
        cur = Node(data[0]+data[1])
        if i ==0:
            cur.left = Node(data[0])
            cur.right = Node(data[1])
            curDic[cur.name] = cur
        elif data[0] in curDic and data[1] in curDic:
            cur.left = curDic[data[0]]
            cur.right = curDic[data[1]]
            curDic[cur.name] = cur
            curDic.pop(data[0])
            curDic.pop(data[1])
        elif data[0] in curDic :
            cur.left = curDic[data[0]]
            cur.right = Node(data[1])
            curDic[cur.name] = cur
            curDic.pop(data[0])
        elif data[1] in curDic:
            cur.left = Node(data[0])
            cur.right = curDic[data[1]]
            curDic[cur.name] = cur
            curDic.pop(data[1])
        else:
            cur.left = Node(data[0])
            cur.right = Node(data[1])
            curDic[cur.name] = cur
        data.append(data[0]+data[1])
        data.pop(0)
        data.pop(0)
    return curDic[data[0]]


def draw(node,data):   # Draw a node as root
    saw = defaultdict(int)

    def create_graph(G, node, p_name ="initvalue", pos={}, x=0, y=0, layer=1):
        if not node:
            return
        name = str(node.name)
        print("node.name:",name,"x,y:(",x,",",y,")l_layer:",layer)
        saw[name] += 1
        if name in saw.keys():
            name += ' ' * saw[name]
        if p_name != "initvalue" :
            G.add_edge(p_name, name)
        pos[name] = (x, y)

        l_x, l_y = x - 1 / (3 * layer), y - 1
        #print("l_x, l_y:",l_x, l_y)
        l_layer = layer + 1
        #print("l_layer:",l_layer)
        create_graph(G, node.left, name, x=l_x, y=l_y, pos=pos, layer=l_layer)

        r_x, r_y = x + 1 /( 3 * layer), y - 1
        #print("r_x, r_y:", r_x, r_y)
        r_layer = layer + 1
        create_graph(G, node.right,name, x=r_x, y=r_y, pos=pos, layer=r_layer)
        return (G, pos)

    graph = nx.DiGraph()
    graph.name
    graph, pos = create_graph(graph, node)
    #pos["     "] = (0, 0)
    print("pos:",pos)
    fig, ax = plt.subplots(figsize=(8, 10))  # Scale can be adjusted appropriately according to the depth of the tree
    color_map = []
    # for j,node in enumerate(graph.nodes):
    for degree in graph.out_degree:
        if int(degree[0]) in data and degree[1] == 0 :
            color_map.append('blue')
        else:
            color_map.append('green')
    #nx.draw(G, node_color=color_map, with_labels=True)
    nx.draw_networkx(graph, pos, ax=ax, node_size=1000,node_color=color_map)
    plt.show()

def huffmanCode(tree,length):
    node = tree
    if not node:
        return
    elif not node.left and not node.right:
        x = str(node.name) + 'Coded as:'
        for i in range(length):
            x += str(b[i])
        dicDeepth[node.name] = x
        print(x)
        return
    b[length] = 0
    huffmanCode(node.left, length + 1)
    b[length] = 1
    huffmanCode(node.right, length + 1)

if __name__ == "__main__":
    # bi_tree = ['hello', 'world', 'I', 'exist', 'because', 'I', 'think','hello', 'world', 'I', 'exist', 'because', 'I', 'think']
    # root = create(bi_tree)

    lista = [2, 9,10, 11, 18, 25]
    root = create(copy.deepcopy(lista))
    huffmanCode(root,0)
    draw(root,lista)

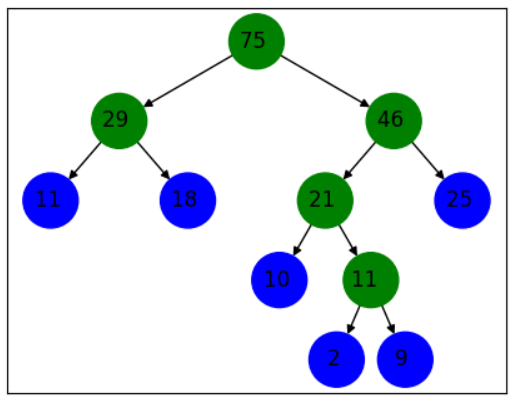
For testing purposes, a special use case is used to illustrate the result in the following figure. There will be two 11 in the tree generation process, but actually one is the value of the node and the other is the value in the rule calculation process, so this should be noted.

summary

The algorithm is endless, read the following code:
This article does not explain the basic principles in detail, the basic principles Grey Brother said very clearly, but used the language of python to achieve it by hand, I suggest you also do more to knock, others may not necessarily understand, but there will always be gains if you knock once.
Recently, I studied recording videos and had time to share Coding videos later.