The code involved in this article has been placed in my github--> link

python implements basic data structures (1)
python implements the underlying data structure (2)
python implements basic data structures (3)

python syntax is more concise, just recently reviewing the data structure, so use python to implement it_
This paper implements linear table, stack, queue, string, binary tree, graph, sorting algorithm.Referring to the textbook is the data structure (C language version) Tsinghua University Press, as well as some of the online views of the great gods.Because it contains code, it is a lot of content, divided into several sections, let's not say more, we go directly to the topic

Note: The experimental environment for this article: Anaconda integration python 3.6.5 (so the code is Python 3)
Since there is too much code in this article, we will not cover each step in detail. I will try to explain the details in the code, and I hope you understand.

Sorting algorithm

It is divided into external sorting and internal sorting. We only talk about internal sorting here. It refers to the sorting process in which the records to be sorted are stored in the computer random memory. There are ten commonly used sorting algorithms. The first six are commonly used, the last four are for understanding only, and the stability and instability depend on whether or not the code is executed or not.Will destroy the order in which parts of the original already exist, for example, 5,1,2...An exchange of 1 and 2 during execution is called instability.First come to the conclusion_
(The following motion picture is taken from https://blog.csdn.net/zhangshk_/article/details/82911093 First thank the big man for his intuitive and clear sorting)

Sorting method; Average time; Best time; Worst time	 	 
Bubble sorting (stable) O(n^2) O(n) O(n^2)
Select Sort (Unstable) O(n^2) O (n^2) O(n^2) O (n^2)
Insert Sort (Stable) O(n^2) O(n) O(n^2)
Hill Sort (Unstable) O(n^1.25)
Merge Sort (Stable) O(nlogn) O (nlogn) O(nlogn)
Quick Sort (Unstable) O(nlogn) O (nlogn) O(n^2)
Heap sorting (unstable) O(nlogn) O (nlogn) O(nlogn)
Count sorting (stable) O(n)											
Bucket sorting (unstable) O(n) O(n) O(n)O(n)
Cardinal sorting (stable) O(n) O(n) O(n) O(n)

Attachment: O(1) < O(logn) < O(n) < O(n logn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
The fastest sorting algorithm is bucket sorting, but it has a lot of drawbacks, so fast sorting uses more

Bubble sort

It repeatedly visits the column of elements to sort, comparing two adjacent elements in turn, and swapping them if their order (for example, from large to small, and from A to Z) is wrong.The work of visiting an element is repeated until no adjacent elements need to be exchanged, that is, the element column has been sorted.
The name of this algorithm comes from the fact that the larger elements will slowly "float" to the top of the array (ascending or descending) by exchange, just as the bubbles of carbon dioxide in a carbonated drink will eventually float to the top, hence the name "bubble sort".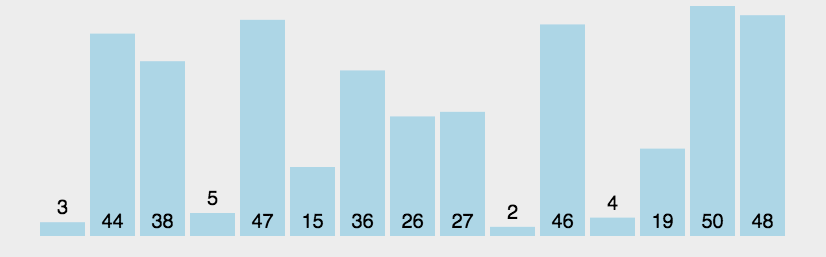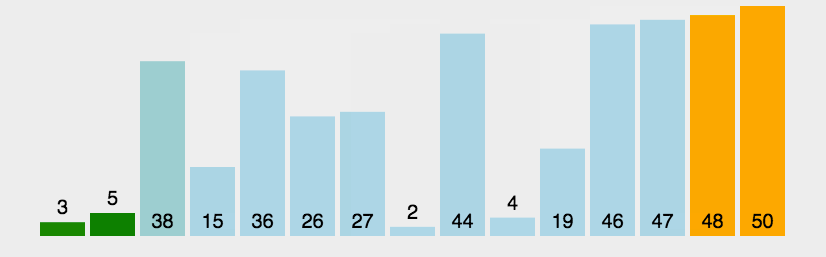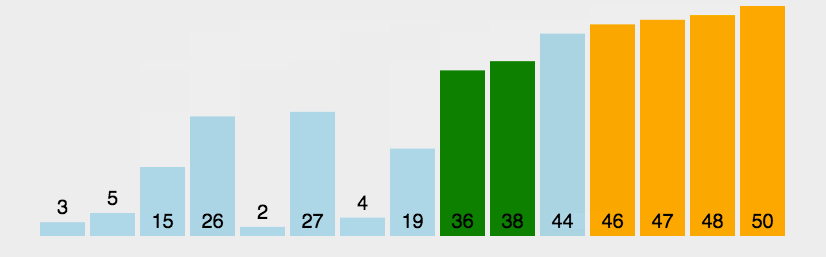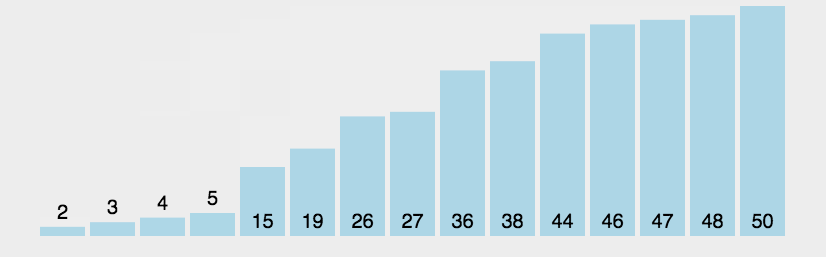

Bubble sorting is simple, code:

def bubbleSort(nums):
    '''Bubble sort ''
    for i in range(len(nums) - 1): 
        for j in range(len(nums) - i - 1): # Ordered sections do not need to be traversed again
            if nums[j] > nums[j+1]:
                nums[j], nums[j+1] = nums[j+1], nums[j] 
    return nums

Select Sort

Selection sort is a simple and intuitive sorting algorithm.It works by first selecting the smallest (or largest) element from the data elements to be sorted, storing it at the beginning of the sequence, then finding the smallest (largest) element from the remaining unsorted elements, and placing it at the end of the sorted sequence.And so on until all the data elements to be sorted have zero number.Selective sorting is an unstable sorting method.

Code_

def selectionSort(nums):
    '''Select Sort'''
    for i in range(len(nums) - 1):  # Traverse len (nums) - once
        minIndex = i
        for j in range(i + 1, len(nums)):
            if nums[j] < nums[minIndex]:  # Update Minimum Index
                minIndex = j  
        nums[i], nums[minIndex] = nums[minIndex], nums[i] # Swap Minimum to Front
    return nums

Insert Sort

Insertion sort is a simple, intuitive and stable sorting algorithm.The basic operation is to insert a record into an ordered table that has been ordered so that a new ordered table can be obtained.The basic idea of insert sorting is to insert one record to be sorted at each step into the appropriate location in the previously sorted file by its key value size until all are inserted.It is a stable sorting algorithm.(viii)

The code is as follows:

def insertionSort(nums):
    '''Insert Sort'''
    for i in range(len(nums) - 1):  # Traverse len (nums) - once
        curNum, preIndex = nums[i+1], i  # curNum saves the current number to insert
        while preIndex >= 0 and curNum < nums[preIndex]: # Move elements larger than curNum backwards
            nums[preIndex + 1] = nums[preIndex]
            preIndex -= 1
        nums[preIndex + 1] = curNum  # The correct position of the number to be inserted   
    return nums

Shell Sort

As the name implies, this is Hill's proposed algorithm, an improved version of insert sort, also known as the descending incremental sort algorithm.The basic idea is that the whole sequence of records to be arranged is separated into several subsequences and sorted directly by insertion. When the records in the whole sequence are basically ordered, the whole records are sorted directly by insertion.
Hill ordering is an improvement based on the following two properties of insertion ordering:

• Insert Sorting is efficient when operating on data that is almost sorted to achieve linear sorting efficiency
• But insert sorting is generally inefficient because insert sorting can only move data one bit at a time
  
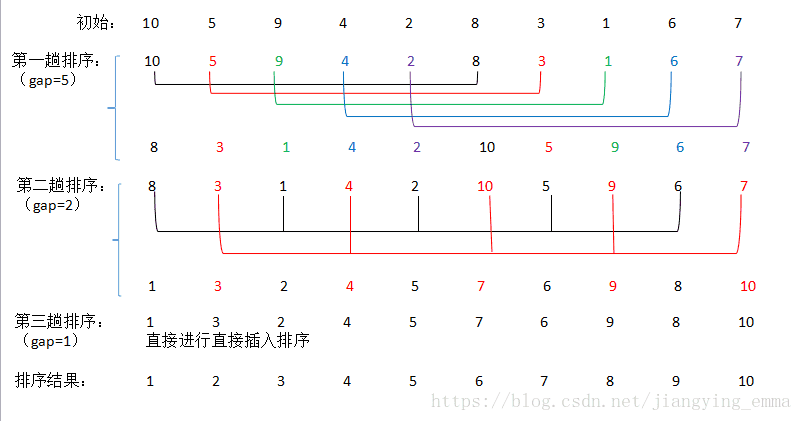
  Attach code:

def shellSort(nums):
    '''Shell Sort'''
    lens = len(nums)
    gap = 1  
    while gap < lens // 3:
        gap = gap * 3 + 1  # Dynamic Definition of Interval Sequences
    while gap > 0:
        for i in range(gap, lens):
            curNum, preIndex = nums[i], i - gap  # curNum saves the current number to insert
            while preIndex >= 0 and curNum < nums[preIndex]:
                nums[preIndex + gap] = nums[preIndex] # Move elements larger than curNum backwards
                preIndex -= gap
            nums[preIndex + gap] = curNum  # The correct position of the number to be inserted
        gap //= 3 #Next dynamic interval
    return nums

Merge Sort

Merge means merging two or more ordered tables into a new ordered table. This is done by Divide and Conquer One of the most typical applications may also be explained in future articles about the algorithm of dividing and conquering. It is worth mentioning that this algorithm was proposed by Von Neumann.The basic idea is similar to that of division and conquer:

• Split: Recursively divide the current sequence into two equal parts.
• Integration: Integrate the subsequences from the previous step together (merge) while maintaining the element order.
  
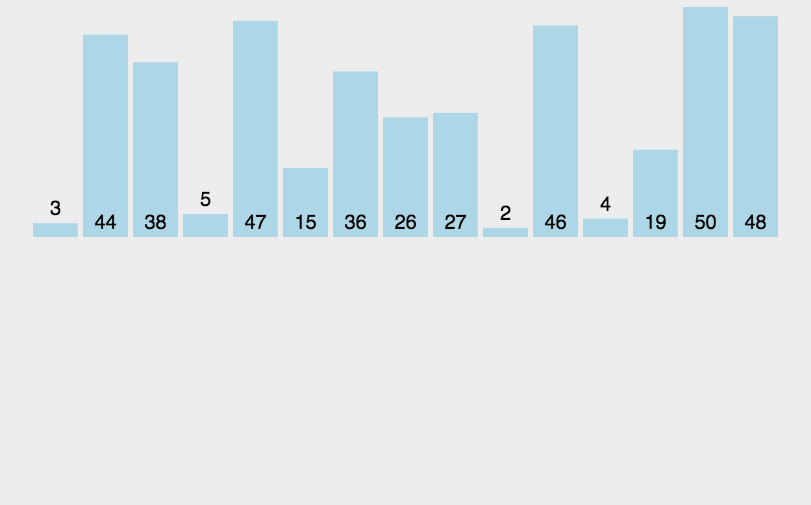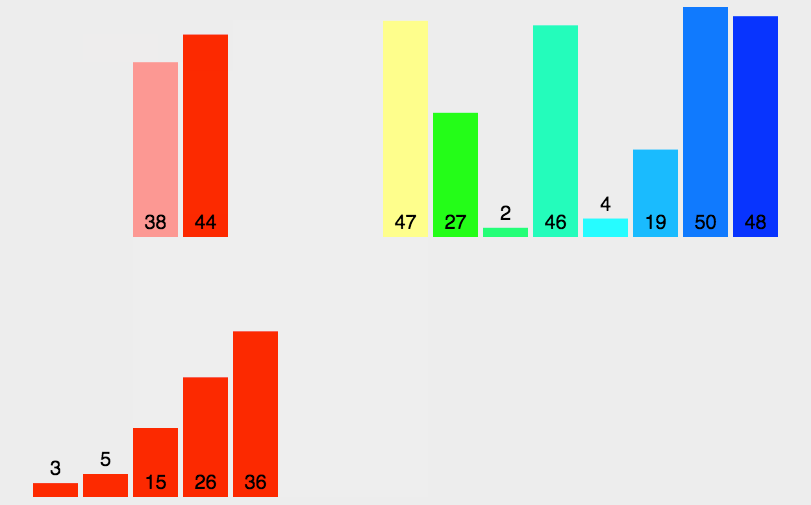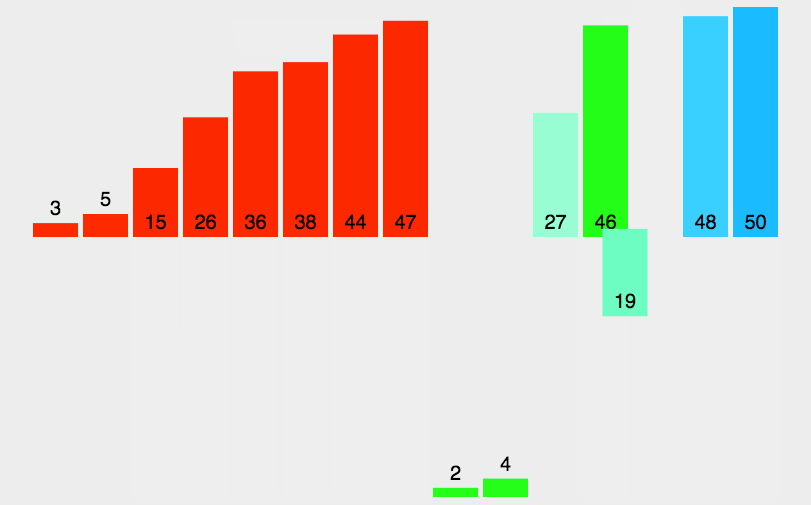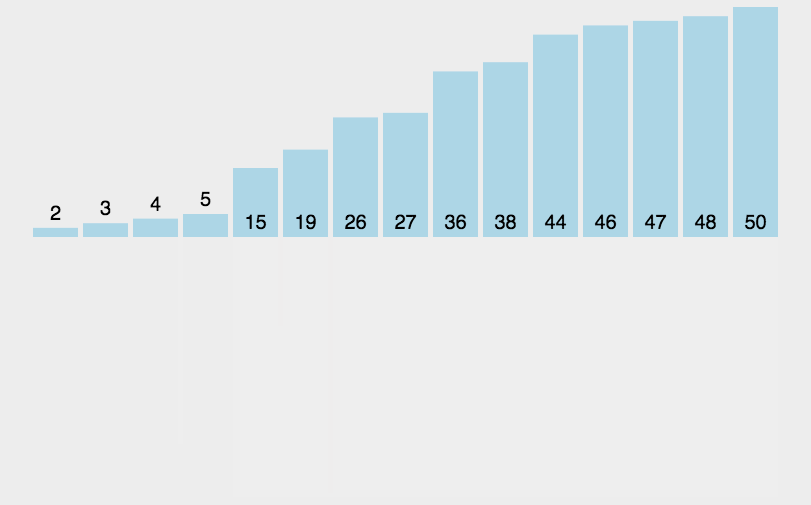
  The code is as follows:

def mergeSort(nums):
    '''Merge Sort'''
    def merge(left, right):
        result = []  
        i = j = 0
        while i < len(left) and j < len(right):
            if left[i] <= right[j]:
                result.append(left[i])
                i += 1
            else:
                result.append(right[j])
                j += 1
        result = result + left[i:] + right[j:] # The remaining elements are added directly to the end
        return result
    if len(nums) <= 1:
        return nums
    mid = len(nums) // 2
    left = mergeSort(nums[:mid])
    right = mergeSort(nums[mid:])
    return merge(left, right)

Quick Sort

This is the sort algorithm that is used most today, and it is basically the sort method used in large data.It is an improved algorithm for bubble sorting. The basic idea is that records to be sorted are separated into two separate parts by one-time sorting. One part of the records has smaller keywords than the other part, so records can be sorted separately for the whole sequence.It is also an application of division and is the most widely used sorting algorithm at present, but note that this is an unstable sorting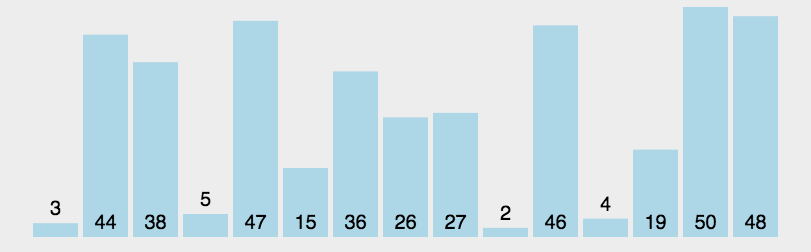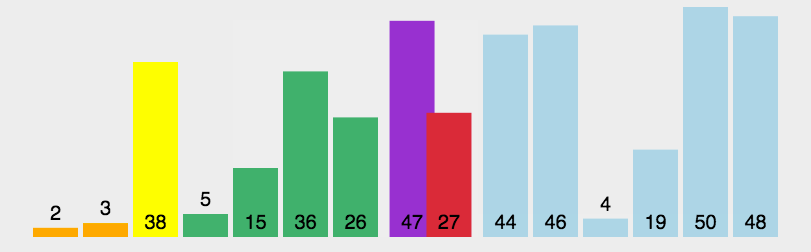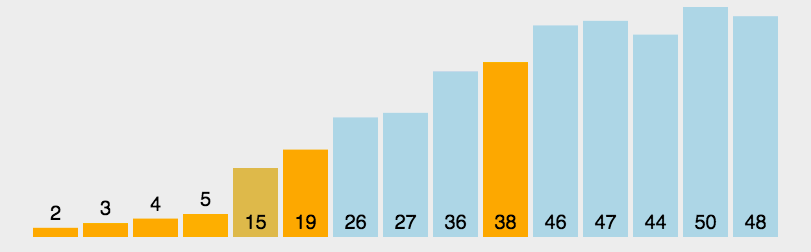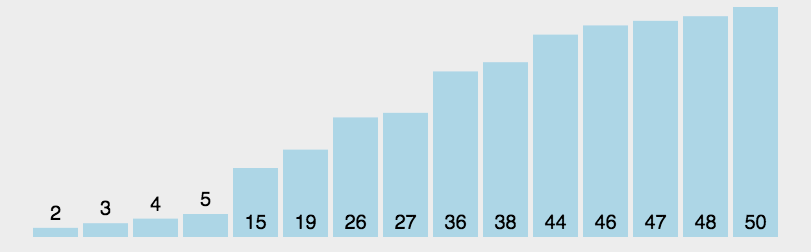

The code is as follows:

def quickSort(nums):  # The average spatial complexity of this writing is O(nlogn)
    '''Quick Sort'''
    if len(nums) <= 1:
        return nums
    pivot = nums[0]  # Baseline value
    left = [nums[i] for i in range(1, len(nums)) if nums[i] < pivot] 
    right = [nums[i] for i in range(1, len(nums)) if nums[i] >= pivot]
    return quickSort(left) + [pivot] + quickSort(right)

Heap Sorting

Heap sorting refers to a sort algorithm designed using the data structure heap.The heap is a nearly complete binary tree structure.A heap is a complete binary tree with the following properties: each node has a value greater than or equal to its left and right child nodes, which is called a large-top heap; or each node has a value less than or equal to its left and right child nodes, which is called a small-top heap.

The basic idea of heap sorting is that the sequence to be sorted is constructed into a large top heap, where the maximum value of the entire sequence is the root node of the top of the heap.Swap it with the end element, where the end is the maximum.The remaining n-1 elements are then reconstructed into a heap, resulting in the minor values of the n elements.By doing this repeatedly, you get an ordered sequence.
Let's look directly at the picture. It may not be easy to understand. Just draw a picture and enjoy it.

The code is as follows:

def heapSort(nums):
    '''Heap Sorting'''
    # Adjust heap
    def adjustHeap(nums, i, size):
        # Left and right children with non-leaf nodes
        lchild = 2 * i + 1
        rchild = 2 * i + 2
        # Find the index of the largest element in the current node, left child, right child
        largest = i 
        if lchild < size and nums[lchild] > nums[largest]: 
            largest = lchild 
        if rchild < size and nums[rchild] > nums[largest]: 
            largest = rchild 
        # If the index of the largest element is not the current node, swap the large node above to continue adjusting the heap
        if largest != i: 
            nums[largest], nums[i] = nums[i], nums[largest] 
            # The second parameter, the index passed into largest, is the index corresponding to the large number before swapping
            # After swapping, the index corresponds to a decimal number, which should be adjusted down
            adjustHeap(nums, largest, size)
    # Build Heap
    def builtHeap(nums, size):
        for i in range(len(nums)//2)[: -1]: #Build a large root heap starting from the first non-leaf node to the last
            adjustHeap(nums, i, size) # Heap adjustment for all non-leaf nodes
        # print(nums)  # Big root heap built for the first time
    # Heap Sorting 
    size = len(nums)
    builtHeap(nums, size) 
    for i in range(len(nums))[::-1]: 
        # Each root node is the maximum number, with the maximum number behind it
        nums[0], nums[i] = nums[i], nums[0] 
        # You need to continue adjusting the heap after swapping, just adjust the root node, where the size of the array does not include the sorted number
        adjustHeap(nums, 0, i) 
    return nums  # Since each large one is placed behind, the last nums are arranged from small to large

Count Sort

Counting sort is a stable linear time sorting algorithm.Count sorting uses an additional array C, where the first element is the number of elements whose median value in the array A to be sorted equals that of i.The elements in A are then positioned correctly according to the array C.Count sorting is not a comparison sort and is faster than any comparison sort algorithm.Although this algorithm is faster, it has many limitations, so it can be understood with less use.
Popular understanding, such as 10 people of different ages, shows that 8 people are younger than A, and A ranks ninth. With this method, you can get everyone else's position, so you can sort them out.Of course, when age is duplicated, special handling is required (stability is guaranteed), which is why the final step is to reverse-populate the target array and subtract 1 from the statistics for each number.The steps of the algorithm are as follows:

• Find the largest and smallest elements in the array to be sorted
• Counts the number of occurrences of each element in the array with a value of i, stored in item I of array C
• Accumulate all counts (starting with the first element in C, adding each item to the previous one)
• Backfill the target array: Place each element I in the C[i] item of the new array, and subtract each element from C[i] by 1.
  
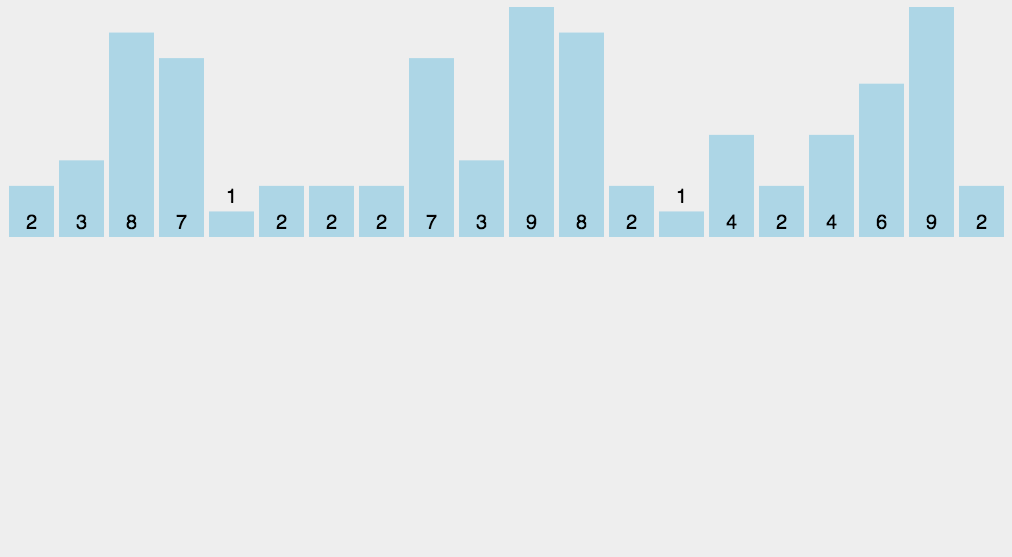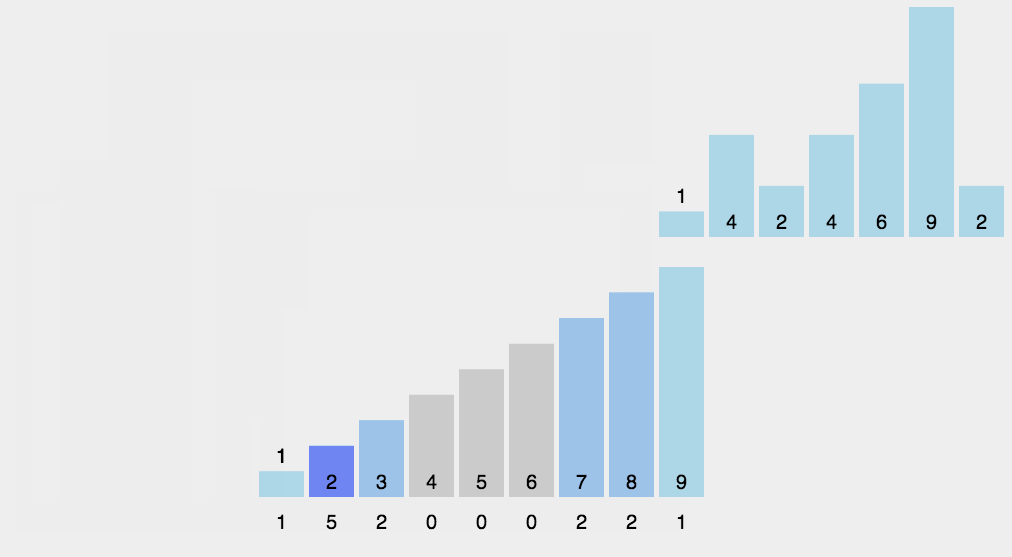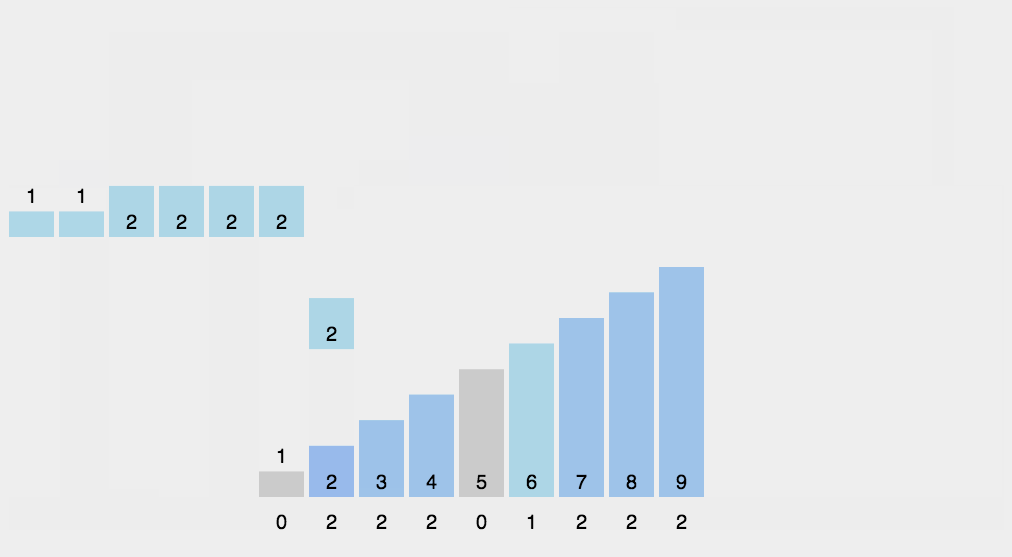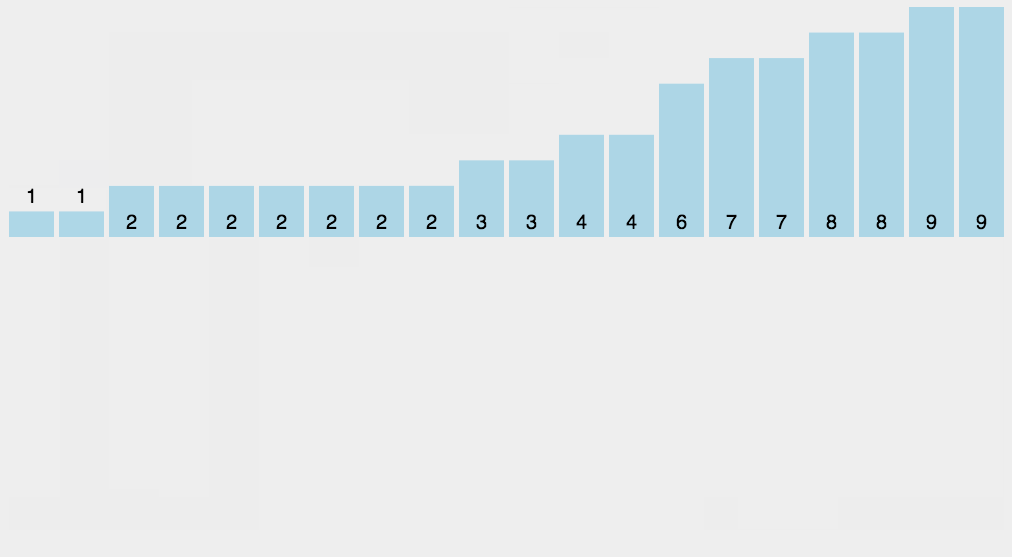
  The code is as follows:

def countingSort(nums):
    '''Count Sort'''
    bucket = [0] * (max(nums) + 1) # Number of buckets
    for num in nums:  # Store element values in buckets as key values and record the number of times they occur
        bucket[num] += 1
    i = 0  # Index of nums
    for j in range(len(bucket)):
        while bucket[j] > 0:
            nums[i] = j
            bucket[j] -= 1
            i += 1
    return nums

Bucket sorting

Bucket sort, or so-called box sort, is a sort algorithm that works by dividing arrays into a limited number of buckets.Each bucket is sorted individually (possibly using a different sorting algorithm or continuing to use bucket sorting recursively).Bucket sorting is not a comparison sort. Bucket sorting is an upgraded version of count sorting.It utilizes the mapping relationship of a function, and the key to its efficiency is the determination of the mapping function.
Bucket sorting should be the fastest sorting method, but because of its large drawbacks, quick sorting is still common_

The code is as follows:

def bucketSort(nums, defaultBucketSize = 5):
    '''Bucket sorting'''
    maxVal, minVal = max(nums), min(nums)
    bucketSize = defaultBucketSize  # If no bucket size is specified, default is 5
    bucketCount = (maxVal - minVal) // BuketSize + 1 #Data is divided into bucketCount groups
    buckets = []  # 2-D Bucket
    for i in range(bucketCount):
        buckets.append([])
    # Use function mapping to put individual data in corresponding buckets
    for num in nums:
        buckets[(num - minVal) // bucketSize].append(num)
    nums.clear()  # Empty nums
    # Sort the elements in each 2-D bucket
    for bucket in buckets:
        insertionSort(bucket)  # Assume insertion sort
        nums.extend(bucket)    # Place sorted buckets in nums in turn
    return nums

Cardinality sorting

At last, I was exhausted.Cardinality sorting is a non-comparative integer sorting algorithm, which uses the principle of cutting integers into different numbers by number and comparing them by number. It achieves this by unifying all the values to be compared (positive integers) into the same number length and filling in zeros before the shorter ones.Then, start with the lowest bit and sort one by one.In this way, the sequence becomes an ordered sequence from the lowest to the highest.Similar to bucket ordering, see picture

The code is as follows:

def radixSort(nums):
    '''Cardinality sorting'''
    mod = 10
    div = 1
    mostBit = len(str(max(nums)))  # The number of maximum digits determines how many times the external circulation occurs
    buckets = [[] for row in range(mod)] # Construct mod empty buckets
    while mostBit:
        for num in nums:  # Put the data in the corresponding bucket
            buckets[num // div % mod].append(num)
        i = 0  # Index of nums
        for bucket in buckets:  # Collect data
            while bucket:
                nums[i] = bucket.pop(0) # Remove in turn
                i += 1
        div *= 10
        mostBit -= 1
    return nums

About testing

I added a time module to roughly compare the time-consuming scenarios, testing the code first (time library is time)

data_test = [23,1,53,654,54,16,65,3,155,506,10, 164, 234, 31, 3, 54,46,654,315]
print('Following the result is the run time(s)')
print('Bubble sort:')
start = time.time()
print(bubbleSort(data_test))
end = time.time()
print(end-start)
print()

print('Select Sort:')
start = time.time()
print(selectionSort(data_test))
end = time.time()
print(end-start)
print()

print('Insert Sort:')
start = time.time()
print(insertionSort(data_test))
end = time.time()
print(end-start)
print()

print('Hill Sort:')
start = time.time()
print(shellSort(data_test))
end = time.time()
print(end-start)
print()

print('Merge Sort:')
start = time.time()
print(mergeSort(data_test))
end = time.time()
print(end-start)
print()

print('Quick Sort:')
start = time.time()
print(quickSort(data_test))
end = time.time()
print(end-start)
print()

print('Heap sorting:')
start = time.time()
print(heapSort(data_test))
end = time.time()
print(end-start)
print()

print('Count sort:')
start = time.time()
print(countingSort(data_test))
end = time.time()
print(end-start)
print()

print('Bucket sorting:')
start = time.time()
print(bucketSort(data_test))
end = time.time()
print(end-start)
print()

print('Cardinal Sort:')
start = time.time()
print(radixSort(data_test))
end = time.time()
print(end-start)

Run result:

Because the amount of data I'm testing here is too small and possibly due to computer reasons, the effect is not obvious, but after running several times, I still find that Quick Sort is the most stable

Finish.Rest