Computers can only understand machine codes. In the final analysis, programming language is just a string of words. The purpose is to make it easier for humans to write what they want computers to do. The real magic is done by compilers and interpreters, which bridge the gap between the two. The interpreter reads the code line by line and converts it into machine code.
In this paper, we will design an interpreter that can perform arithmetic operations.
We won't rebuild the wheel. The article will use a lexical parser, PLY (Python Lex yacc), developed by David M. Beazley( https://github.com/dabeaz/PLY )).
PLY can be downloaded in the following ways:
$ pip install ply
We'll take a cursory look at the basics needed to create an interpreter. For more information, see this GitHub repository( https://github.com/dabeaz/ply).
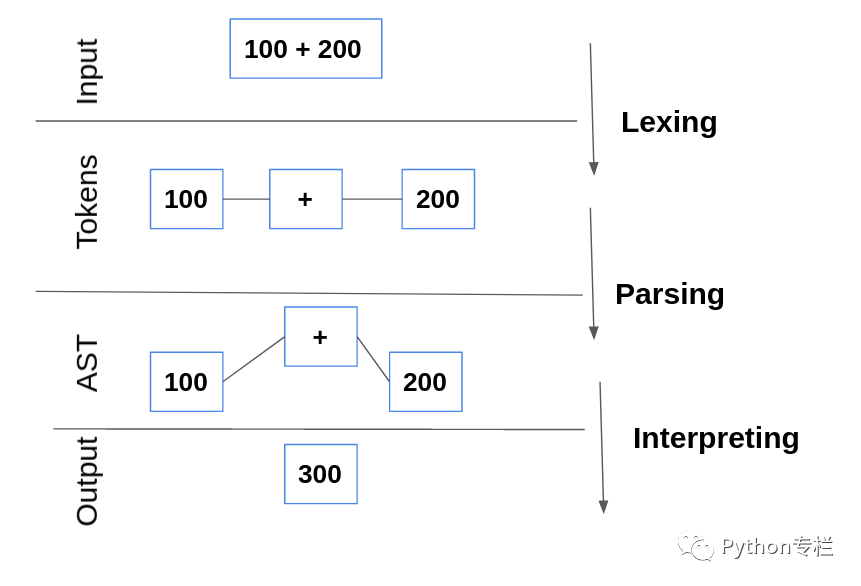
Token
A tag is the smallest character unit that provides meaningful information to the interpreter. The tag contains a pair of names and attribute values.
Let's start by creating a list of tag names. This is a necessary step.
tokens = ( #Data type "NUM", "FLOAT", #Arithmetic operation "PLUS", "MINUS", "MUL", "DIV", #Bracket "LPAREN", "RPAREN", )
Lexical analyzer (Lexer)
The process of converting a statement into a tag is called tokenization or lexical analysis. The program that performs lexical analysis is lexical analyzer.
#Regular expression of markers
t_PLUS = r"\+"
t_MINUS = r"\-"
t_MUL = r"\*"
t_DIV = r"/"
t_LPAREN = r"\("
t_RPAREN = r"\)"
t_POW = r"\^"
#Ignore spaces and tabs
t_ignore = " \t"
#Add actions for each rule
def t_FLOAT(t):
r"""\d+\.\d+"""
t.value = float(t.value)
return t
def t_NUM(t):
r"""\d+"""
t.value = int(t.value)
return t
#Error handling of undefined rule characters
def t_error(t):
#The , t.value , here contains the remaining unmarked inputs
print(f"keyword not found: {t.value[0]}\nline {t.lineno}")
t.lexer.skip(1)
#If \ n , is encountered, it is set as a new row
def t_newline(t):
r"""\n+"""
t.lexer.lineno += t.value.count("\n")
To import the lexical analyzer, we will use:
import ply.lex as lex
t_ Is a special prefix that represents the rule that defines the tag. Each lexical rule is made of regular expression, which is compatible with the re module in Python. Regular expressions can scan input according to rules and search for matching symbol strings. The grammar defined by regular expressions is called regular grammar. The language defined by regular grammar is called regular language.
With the rules defined, we'll build a lexical analyzer.
data = 'a = 2 +(10 -8)/1.0' lexer = lex.lex() lexer.input(data) while tok := lexer.token(): print(tok)
To pass the input string, we use lexer input(data). lexer.token() will return the next LexToken instance, and finally return None. According to the above rules, the mark of code 2 + (10 - 8) / 1.0 will be:

The purple character represents the name of the mark, followed by the specific content of the mark.
Backus Naur form (BNF)
Most programming languages can be written in context free grammar. It is more complex than conventional languages. For context free grammar, we use context free grammar, which is a rule set that describes all possible grammars in the language. BNF is a way to define syntax. It describes the syntax of programming language. Let's look at an example:
symbol : alternative1 | alternative2 ...
According to the production formula, the left side of: is replaced by one of the values on the right. The values on the right are separated by | (it can be understood that symbol is defined as alternative 1 or alternative 2 or... And so on). For our arithmetic interpreter, the syntax specification is as follows:
expression : expression '+' expression | expression '-' expression | expression '/' expression | expression '*' expression | expression '^' expression | +expression | -expression | ( expression ) | NUM | FLOAT
The input marks are symbols such as NUM, FLOAT, +, -, *, /, which are called terminals (characters that cannot continue to decompose or generate other symbols). An expression consists of a terminal and a rule set. For example, expression is called a non terminal.
Parser
We will use YACC (yet another compiler) as the parser generator. Import module: import ply YACC as YACC.
from operator import (add, sub, mul, truediv, pow)
#List of operators supported by our interpreter
ops = {
"+": add,
"-": sub,
"*": mul,
"/": truediv,
"^": pow,
}
def p_expression(p):
"""expression : expression PLUS expression
| expression MINUS expression
| expression DIV expression
| expression MUL expression
| expression POW expression"""
if (p[2], p[3]) == ("/", 0):
#If divided by 0, "INF" (infinite) is taken as the value
p[0] = float("INF")
else:
p[0] = ops[p[2]](p[1], p[3])
def p_expression_uplus_or_expr(p):
"""expression : PLUS expression %prec UPLUS
| LPAREN expression RPAREN"""
p[0] = p[2]
def p_expression_uminus(p):
"""expression : MINUS expression %prec UMINUS"""
p[0] = -p[2]
def p_expression_num(p):
"""expression : NUM
| FLOAT"""
p[0] = p[1]
#Rules for syntax errors
def p_error(p):
print(f"Syntax error in {p.value}")
In the document string, we will add the appropriate syntax specification. The elements in the p list correspond to the syntax symbols one by one, as shown below:
expression : expression PLUS expression p[0] p[1] p[2] p[3]
In the above,% prec UPLUS and% prec UMINUS are used to represent custom operations Prec is the abbreviation of precedence. There is no such thing as UPLUS and UMINUS in the symbols (in this article, these two custom operations represent unary positive signs and symbols. In fact, UPLUS and UMINUS are just names, and they can take whatever they want). After that, we can add expression based rules. YACC allows priority to be assigned to each token. We can set it using the following methods:
precedence = (
("left", "PLUS", "MINUS"),
("left", "MUL", "DIV"),
("left", "POW"),
("right", "UPLUS", "UMINUS")
)
In the priority declaration, tags are arranged in order of priority from low to high. PLUS and MINUS have the same priority and are left associative (operations are performed from left to right). MUL and DIV have higher priority than PLUS and MINUS, and also have left combination. The same is true for POW, but with higher priority. UPLUS and UMINUS have right combination (the operation is executed from right to left).
To parse the input, we will use:
parser = yacc.yacc() result = parser.parse(data) print(result)
The complete code is as follows:
#####################################
# Introduction module #
#####################################
from logging import (basicConfig, INFO, getLogger)
from operator import (add, sub, mul, truediv, pow)
import ply.lex as lex
import ply.yacc as yacc
#List of operators supported by our interpreter
ops = {
"+": add,
"-": sub,
"*": mul,
"/": truediv,
"^": pow,
}
#####################################
# Tag set #
#####################################
tokens = (
#Data type
"NUM",
"FLOAT",
#Arithmetic operation
"PLUS",
"MINUS",
"MUL",
"DIV",
"POW",
#Bracket
"LPAREN",
"RPAREN",
)
#####################################
# Marked regular expression #
#####################################
t_PLUS = r"\+"
t_MINUS = r"\-"
t_MUL = r"\*"
t_DIV = r"/"
t_LPAREN = r"\("
t_RPAREN = r"\)"
t_POW = r"\^"
#Ignore spaces and tabs
t_ignore = " \t"
#Add actions for each rule
def t_FLOAT(t):
r"""\d+\.\d+"""
t.value = float(t.value)
return t
def t_NUM(t):
r"""\d+"""
t.value = int(t.value)
return t
#Error handling of undefined rule characters
def t_error(t):
#The , t.value , here contains the remaining unmarked inputs
print(f"keyword not found: {t.value[0]}\nline {t.lineno}")
t.lexer.skip(1)
#If you see \ n , set it to a new line
def t_newline(t):
r"""\n+"""
t.lexer.lineno += t.value.count("\n")
#####################################
# Set symbol priority #
#####################################
precedence = (
("left", "PLUS", "MINUS"),
("left", "MUL", "DIV"),
("left", "POW"),
("right", "UPLUS", "UMINUS")
)
#####################################
# write BNF rule #
#####################################
def p_expression(p):
"""expression : expression PLUS expression
| expression MINUS expression
| expression DIV expression
| expression MUL expression
| expression POW expression"""
if (p[2], p[3]) == ("/", 0):
#If divided by 0, "INF" (infinite) is taken as the value
p[0] = float("INF")
else:
p[0] = ops[p[2]](p[1], p[3])
def p_expression_uplus_or_expr(p):
"""expression : PLUS expression %prec UPLUS
| LPAREN expression RPAREN"""
p[0] = p[2]
def p_expression_uminus(p):
"""expression : MINUS expression %prec UMINUS"""
p[0] = -p[2]
def p_expression_num(p):
"""expression : NUM
| FLOAT"""
p[0] = p[1]
#Rules for syntax errors
def p_error(p):
print(f"Syntax error in {p.value}")
#####################################
# main program #
#####################################
if __name__ == "__main__":
basicConfig(level=INFO, filename="logs.txt")
lexer = lex.lex()
parser = yacc.yacc()
while True:
try:
result = parser.parse(
input(">>>"),
debug=getLogger())
print(result)
except AttributeError:
print("invalid syntax")
conclusion
Due to the huge volume of this topic, this article can not fully explain things, but I hope you can well understand the surface knowledge covered in the article.
[teacher song song - in class] a complete set of video tutorials on Python foundation, the most classic in history (including source code, notes and homework)
I got it from my little sister
