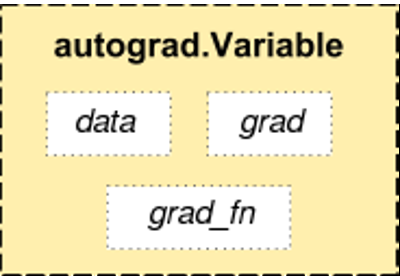
Variable

Tensor is a perfect component in PyTorch, but building neural network is far from enough. We need tensor that can build calculation graph, which is variable. Variable is the encapsulation of tensor. The operation is the same as that of tensor, but each Variabel has three attributes, and the tensor itself in variable data, corresponding to the gradient of tensor Grad and how this variable is obtained grad_fn

There is no difference between Variable and tensor in essence, but Variable will be put into a calculation diagram, and then forward propagation, back propagation and automatic derivation will be carried out. First, the Variable is in torch autograd. In variables, it is also very simple to turn a tensor into a Variable. For example, if you want to turn a tensor a into a Variable, you only need Variable(a).

Variable contains three attributes:

• Data: Tensor is stored, which is ontology data-
• grad: the gradient of data is saved. It is a Variable instead of Tensor, which is consistent with the shape of data
• grad_fn: refers to the Function object, which is used for gradient calculation of back propagation
  

# Import variables in the following way
from torch.autograd import Variable

x_tensor = torch.randn(10, 5)
y_tensor = torch.randn(10, 5)

# Change tensor to Variable
x = Variable(x_tensor, requires_grad=True) # The default Variable does not need to be graded, so we use this method to declare that it needs to be graded
y = Variable(y_tensor, requires_grad=True)

z = torch.sum(x + y)

print(z.data)
print(z.grad_fn)

tensor(-18.1752)
<SumBackward0 object at 0x000001DD2D2E2448>

Above, we hit the tensor value in z and passed grad_fn knows that it is obtained through Sum

# Find the gradient of x and y
z.backward()

print(x.grad)
print(y.grad)

tensor([[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]])
tensor([[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]])

Pass grad, we get the gradients of x and y. here we use the automatic derivation mechanism provided by PyTorch, which is very convenient

Example (scalar derivative)

# Create Variable
x = Variable(torch.Tensor([1]), requires_grad=True)
w = Variable(torch.Tensor([2]), requires_grad=True)
b = Variable(torch.Tensor([3]), requires_grad=True)

# Build a computational graph
y = w * x + b # y = 2x + b

# Compute gradients
y.backward() # same as y.backward(torch.FloatTensor([1]))
# Print out the gradients.
print(x.grad)  # x.grad = 2
print(w.grad)  # w.grad = 1
print(b.grad)  # b.grad = 1

tensor([2.])
tensor([1.])
tensor([1.])

Matrix Calculus

x = torch.randn(3)
x = Variable(x, requires_grad=True)
print(x)

y = x * 2
print(y)

y.backward(torch.FloatTensor([1, 0.1, 0.01]))
print(x.grad)

tensor([-2.0131, -1.9689, -0.7120], requires_grad=True)
tensor([-4.0262, -3.9377, -1.4241], grad_fn=)
tensor([2.0000, 0.2000, 0.0200])

It is equivalent to giving a three-dimensional vector for operation. At this time, the result y is a vector. Here, the derivation of this vector cannot be directly written as y.backward(), so the program will report an error. At this time, you need to pass in parameter declarations, such as y.backward(torch.FloatTensor([1, 1, 1]), so that the result is the gradient of each component, or you can pass in y.backward(torch.FloatTensor([1, 0.1, 0.01]), so that the gradient is their original gradient multiplied by 1, 0.1 and 0.01 respectively.

Little practice

Try to build a function y = x 2 y = x^2 y=x2, and then find the derivative of x=2.

Reference output: 4

Tips:
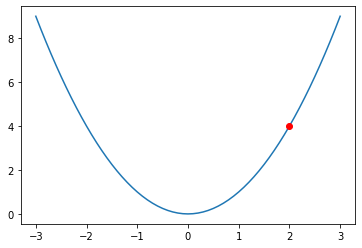
y = x 2 y = x^2 The image of y=x2 is as follows

import matplotlib.pyplot as plt
x = np.arange(-3, 3.01, 0.1)
y = x ** 2
plt.plot(x, y)
plt.plot(2, 4, 'ro')
plt.show()

# answer
x = Variable(torch.FloatTensor([2]), requires_grad=True)
y = x ** 2
y.backward()
print(x.grad)

tensor([4.])