SARIMA(p,d,q)(P,D,Q,s) seasonal autoregressive moving average model has seven structural parameters
AR(p) autoregressive model, i.e. use oneself to regress oneself.
The basic assumption is that the current sequence value depends on its previous value with time delay. The maximum lag in the model is recorded as p
To determine the initial p, you need to look at the PACF graph and find the largest significant lag, after which most of the other lags become irrelevant.
MA(q) moving average model is to model the error of time series, and assume that the current error depends on the error with delay. The initial value can be found on the ACF graph.
Combining the above two methods: AR(p)+MA(q)=ARMA(p,q)AR(p)+MA(q)=ARMA(p,q)AR(p)+MA(q)=ARMA(p,q), which is the autoregressive moving average model
Remaining parameters:
I(d)
- order of integration. This is simply the number of nonseasonal differences needed to make the series stationary. In our case, it's just 1 because we used first differences.
Adding this letter to the four gives us the ARIMA
model which can handle non-stationary data with the help of nonseasonal differences. Great, one more letter to go!
S(s)
- this is responsible for seasonality and equals the season period length of the series
With this, we have three parameters: (P,D,Q)
P
- order of autoregression for the seasonal component of the model, which can be derived from PACF. But you need to look at the number of significant lags, which are the multiples of the season period length. For example, if the period equals 24 and we see the 24-th and 48-th lags are significant in the PACF, that means the initial P
should be 2.
Q
- similar logic using the ACF plot instead.
D
- order of seasonal integration. This can be equal to 1 or 0, depending on whether seasonal differeces were applied or not.
OK, let's use SARIMA to model A kind of
Import package
import warnings # do not disturbe mode warnings.filterwarnings('ignore') # Load packages import numpy as np # vectors and matrices import pandas as pd # tables and data manipulations import matplotlib.pyplot as plt # plots import seaborn as sns # more plots from dateutil.relativedelta import relativedelta # working with dates with style from scipy.optimize import minimize # for function minimization import statsmodels.formula.api as smf # statistics and econometrics import statsmodels.tsa.api as smt import statsmodels.api as sm import scipy.stats as scs from itertools import product # some useful functions from tqdm import tqdm_notebook # Importing everything from forecasting quality metrics from sklearn.metrics import r2_score, median_absolute_error, mean_absolute_error from sklearn.metrics import median_absolute_error, mean_squared_error, mean_squared_log_error
# MAPE def mean_absolute_percentage_error(y_true, y_pred): return np.mean(np.abs((y_true - y_pred) / y_true)) * 100 def tsplot(y, lags=None, figsize=(12, 7), style='bmh'): """ Plot time series, its ACF and PACF, calculate Dickey–Fuller test y - timeseries lags - how many lags to include in ACF, PACF calculation """ if not isinstance(y, pd.Series): y = pd.Series(y) with plt.style.context(style): fig = plt.figure(figsize=figsize) layout = (2, 2) ts_ax = plt.subplot2grid(layout, (0, 0), colspan=2) acf_ax = plt.subplot2grid(layout, (1, 0)) pacf_ax = plt.subplot2grid(layout, (1, 1)) y.plot(ax=ts_ax) p_value = sm.tsa.stattools.adfuller(y)[1] ts_ax.set_title('Time Series Analysis Plots\n Dickey-Fuller: p={0:.5f}'.format(p_value)) smt.graphics.plot_acf(y, lags=lags, ax=acf_ax) smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax) plt.tight_layout()
Read data
ads = pd.read_csv('ads.csv', index_col=['Time'], parse_dates=['Time'])
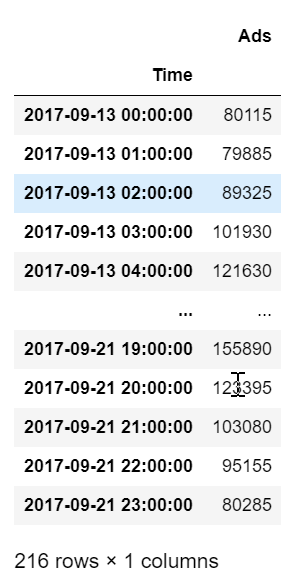
plt.figure(figsize=(18, 6)) plt.plot(ads.Ads) plt.title('Ads watched (hourly data)') plt.grid(True) plt.show()
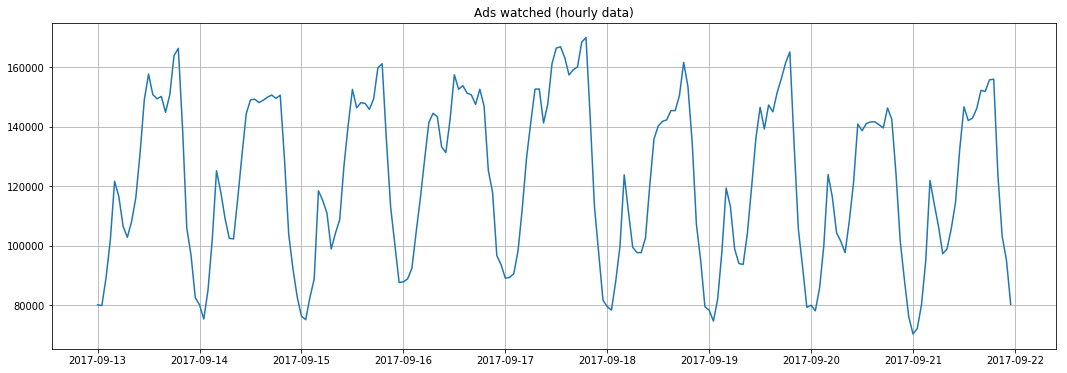
tsplot(ads.Ads, lags=60)
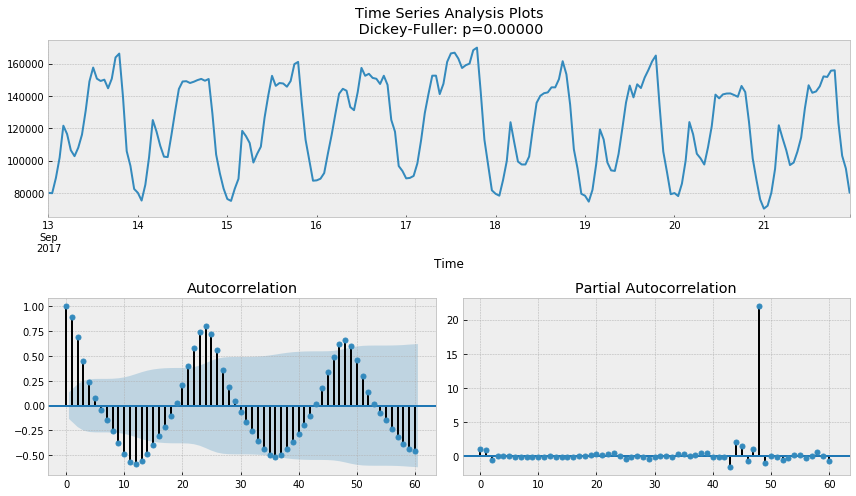
# The seasonal difference ads_diff = ads.Ads - ads.Ads.shift(24) tsplot(ads_diff[24:], lags=60)
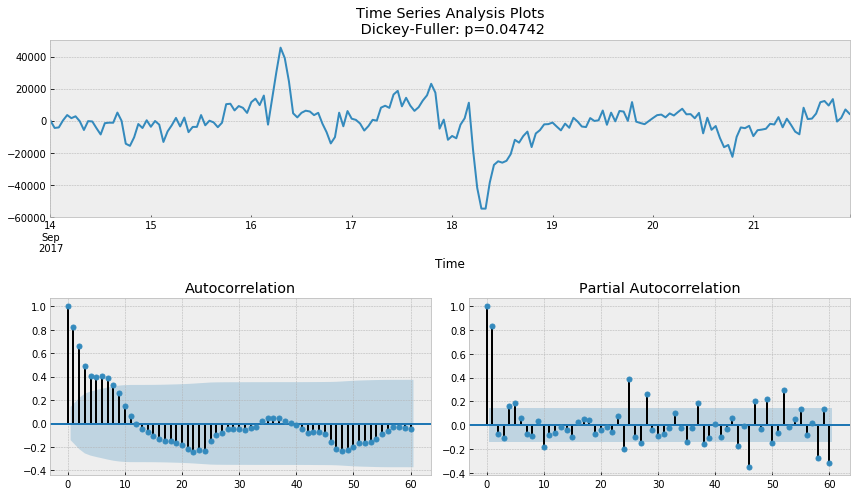
ads_diff = ads_diff - ads_diff.shift(1) tsplot(ads_diff[24+1:], lags=60)
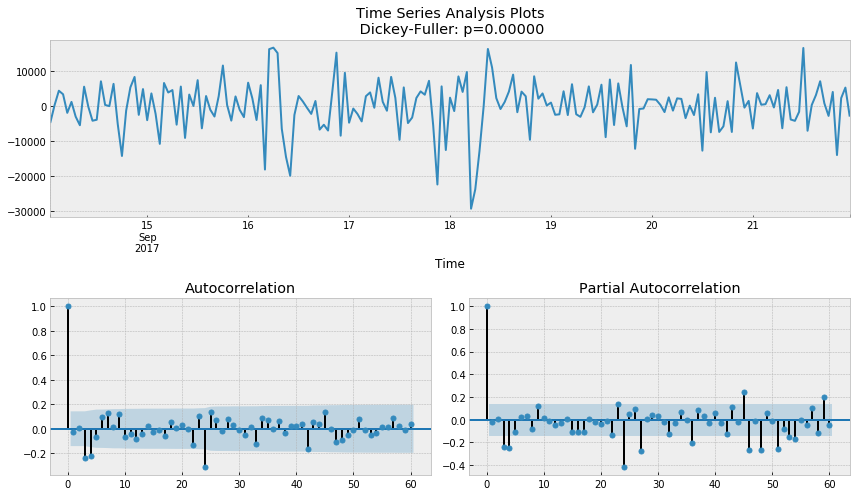
SARIMA parameter
- p is 4 because the last significant lag on the PACF, after which most of the others were not significant.
- d is 1 because of the first order difference
- q according to ACF, it should be about 4
- P may be 2, because the lag of 24 and 48 is important in PACF
- D is 1 because we do the seasonal difference
- Q may be 1, the 24th lag of ACF is obvious, while the 48th lag is not
# setting initial values and some bounds for them ps = range(2, 5) d=1 qs = range(2, 5) Ps = range(0, 2) D=1 Qs = range(0, 2) s = 24 # season length is still 24 # creating list with all the possible combinations of parameters parameters = product(ps, qs, Ps, Qs) parameters_list = list(parameters) len(parameters_list) # 36
Adjust parameters according to AIC
def optimizeSARIMA(parameters_list, d, D, s): """Return dataframe with parameters and corresponding AIC parameters_list - list with (p, q, P, Q) tuples d - integration order in ARIMA model D - seasonal integration order s - length of season """ results = [] best_aic = float("inf") for param in tqdm_notebook(parameters_list): # we need try-except because on some combinations model fails to converge try: model=sm.tsa.statespace.SARIMAX(ads.Ads, order=(param[0], d, param[1]), seasonal_order=(param[2], D, param[3], s)).fit(disp=-1) except: continue aic = model.aic # saving best model, AIC and parameters if aic < best_aic: best_model = model best_aic = aic best_param = param results.append([param, model.aic]) result_table = pd.DataFrame(results) result_table.columns = ['parameters', 'aic'] # sorting in ascending order, the lower AIC is - the better result_table = result_table.sort_values(by='aic', ascending=True).reset_index(drop=True) return result_table
warnings.filterwarnings("ignore") result_table = optimizeSARIMA(parameters_list, d, D, s) ''' parameters aic 0 (2, 3, 1, 1) 3888.642174 1 (3, 2, 1, 1) 3888.763568 2 (4, 2, 1, 1) 3890.279740 3 (3, 3, 1, 1) 3890.513196 4 (2, 4, 1, 1) 3892.302849 5 (4, 3, 1, 1) 3892.322855 6 (3, 4, 1, 1) 3893.762846 7 (4, 4, 1, 1) 3894.327967 8 (2, 2, 1, 1) 3894.798147 9 (2, 3, 0, 1) 3897.170902 10 (3, 2, 0, 1) 3897.815032 11 (4, 2, 0, 1) 3899.073591 12 (3, 3, 0, 1) 3899.165271 13 (3, 4, 0, 1) 3900.500309 14 (2, 4, 0, 1) 3900.502494 15 (4, 3, 0, 1) 3901.255700 16 (4, 4, 0, 1) 3902.650501 17 (2, 2, 0, 1) 3903.905714 18 (2, 3, 1, 0) 3909.281188 19 (3, 2, 1, 0) 3909.502838 20 (4, 2, 1, 0) 3910.927759 21 (3, 3, 1, 0) 3911.192654 22 (3, 4, 1, 0) 3911.344351 23 (2, 4, 1, 0) 3911.809710 24 (4, 4, 1, 0) 3913.084053 25 (4, 3, 1, 0) 3913.409057 26 (2, 2, 1, 0) 3914.786853 27 (3, 2, 0, 0) 3925.433806 28 (2, 2, 0, 0) 3925.786566 29 (2, 3, 0, 0) 3925.879649 30 (2, 4, 0, 0) 3926.311190 31 (3, 3, 0, 0) 3927.427240 32 (4, 2, 0, 0) 3927.427417 33 (3, 4, 0, 0) 3928.376406 34 (4, 3, 0, 0) 3929.059361 35 (4, 4, 0, 0) 3930.078725 '''
# set the parameters that give the lowest AIC p, q, P, Q = result_table.parameters[0] best_model=sm.tsa.statespace.SARIMAX(ads.Ads, order=(p, d, q), seasonal_order=(P, D, Q, s)).fit(disp=-1) print(best_model.summary()) ''' Statespace Model Results ========================================================================================== Dep. Variable: Ads No. Observations: 216 Model: SARIMAX(2, 1, 3)x(1, 1, 1, 24) Log Likelihood -1936.321 Date: Sat, 07 Mar 2020 AIC 3888.642 Time: 15:00:14 BIC 3914.660 Sample: 09-13-2017 HQIC 3899.181 - 09-21-2017 Covariance Type: opg ============================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------ ar.L1 0.7913 0.270 2.928 0.003 0.262 1.321 ar.L2 -0.5503 0.306 -1.799 0.072 -1.150 0.049 ma.L1 -0.7316 0.262 -2.793 0.005 -1.245 -0.218 ma.L2 0.5651 0.282 2.005 0.045 0.013 1.118 ma.L3 -0.1811 0.092 -1.964 0.049 -0.362 -0.000 ar.S.L24 0.3312 0.076 4.351 0.000 0.182 0.480 ma.S.L24 -0.7635 0.104 -7.361 0.000 -0.967 -0.560 sigma2 4.574e+07 5.61e-09 8.15e+15 0.000 4.57e+07 4.57e+07 =================================================================================== Ljung-Box (Q): 43.70 Jarque-Bera (JB): 10.56 Prob(Q): 0.32 Prob(JB): 0.01 Heteroskedasticity (H): 0.65 Skew: -0.28 Prob(H) (two-sided): 0.09 Kurtosis: 4.00 =================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step). [2] Covariance matrix is singular or near-singular, with condition number 1.08e+32. Standard errors may be unstable. '''
tsplot(best_model.resid[24+1:], lags=60)
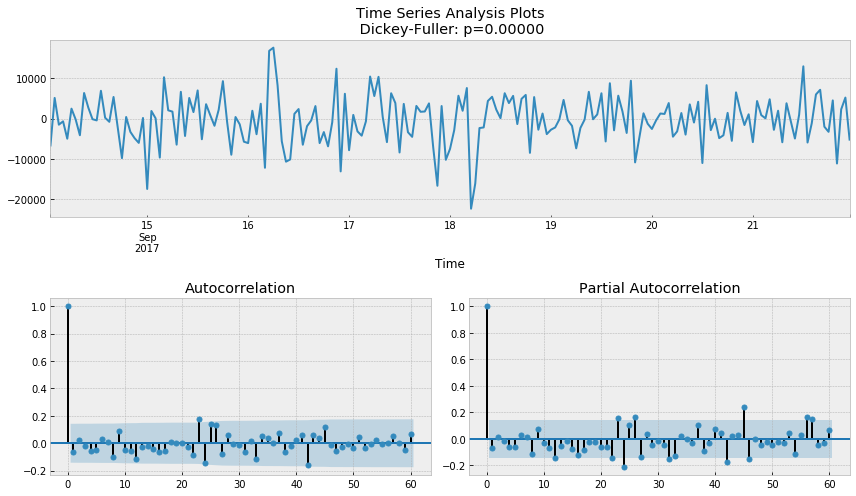
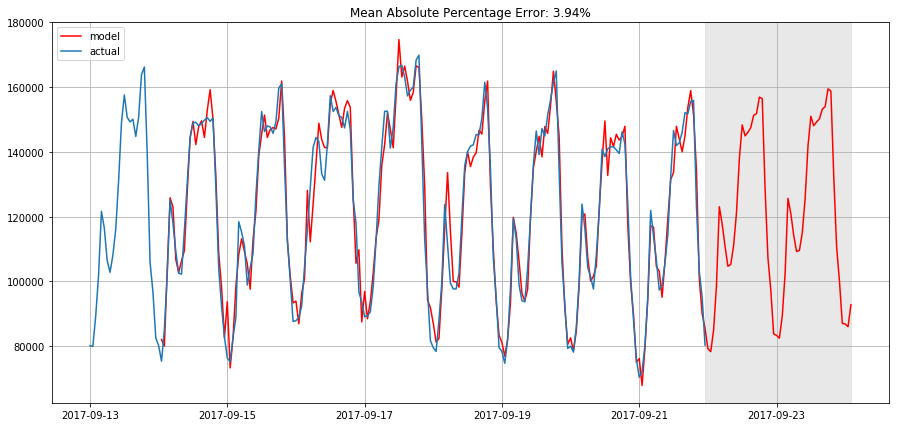
def plotSARIMA(series, model, n_steps): """Plots model vs predicted values series - dataset with timeseries model - fitted SARIMA model n_steps - number of steps to predict in the future """ # adding model values data = series.copy() data.columns = ['actual'] data['sarima_model'] = model.fittedvalues # making a shift on s+d steps, because these values were unobserved by the model # due to the differentiating data['sarima_model'][:s+d] = np.NaN # forecasting on n_steps forward forecast = model.predict(start = data.shape[0], end = data.shape[0]+n_steps) forecast = data.sarima_model.append(forecast) # calculate error, again having shifted on s+d steps from the beginning error = mean_absolute_percentage_error(data['actual'][s+d:], data['sarima_model'][s+d:]) plt.figure(figsize=(15, 7)) plt.title("Mean Absolute Percentage Error: {0:.2f}%".format(error)) plt.plot(forecast, color='r', label="model") plt.axvspan(data.index[-1], forecast.index[-1], alpha=0.5, color='lightgrey') plt.plot(data.actual, label="actual") plt.legend() plt.grid(True)
plotSARIMA(ads, best_model, 50)