BFS
What is BFS
BFS is called breadth first search, also called breadth first search. Its alias is BFS, which belongs to a blind search method.
Dijkstra single source shortest path algorithm and Prim minimum spanning tree algorithm adopt the idea similar to width first search.
The purpose is to systematically expand and check all nodes in the diagram to find the results.
In other words, it does not consider the possible location of the result and searches the whole graph thoroughly until it finds the result.
Its idea is to start from a vertex V0 and traverse the wider area around it radially, so it is named.
Breadth first search is realized by using queue, which has the characteristics of first in first out FIFO(First Input First Output).
Working process and principle of BPS
BFS operation steps are as follows:
1. Put the starting point into the queue;
2. Repeat the following 2 steps until the queue is empty:
1) Take out the queue header from the queue;
2) Find the points adjacent to this point that have not been traversed, mark them, and then put them all into the queue.
(1) Put the starting node 1 into the queue and mark it as traversed:
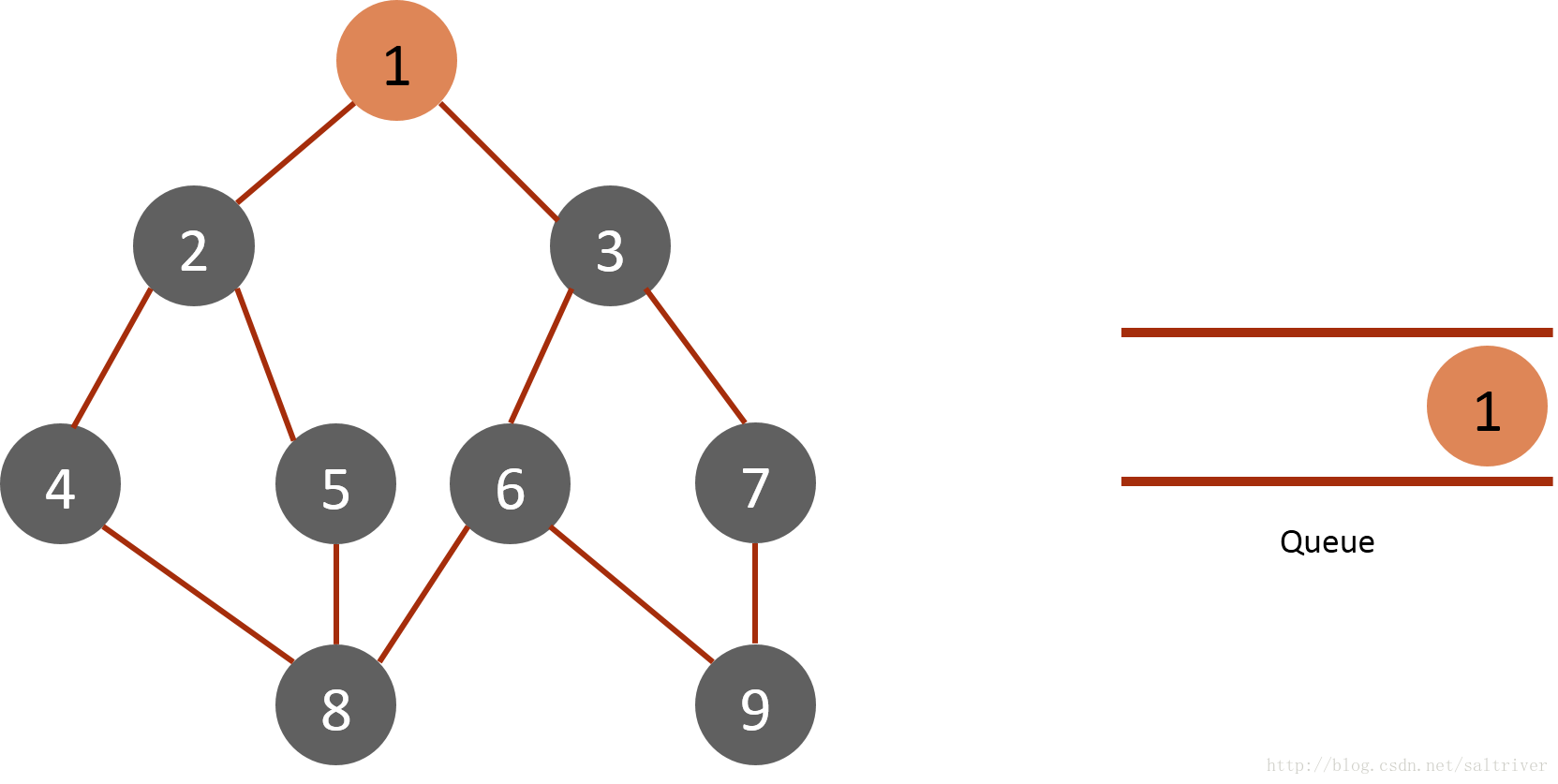
(2) Take node 1 of the queue header from the queue, find nodes 2 and 3 adjacent to node 1, mark them as traversed, and then put them into the queue.
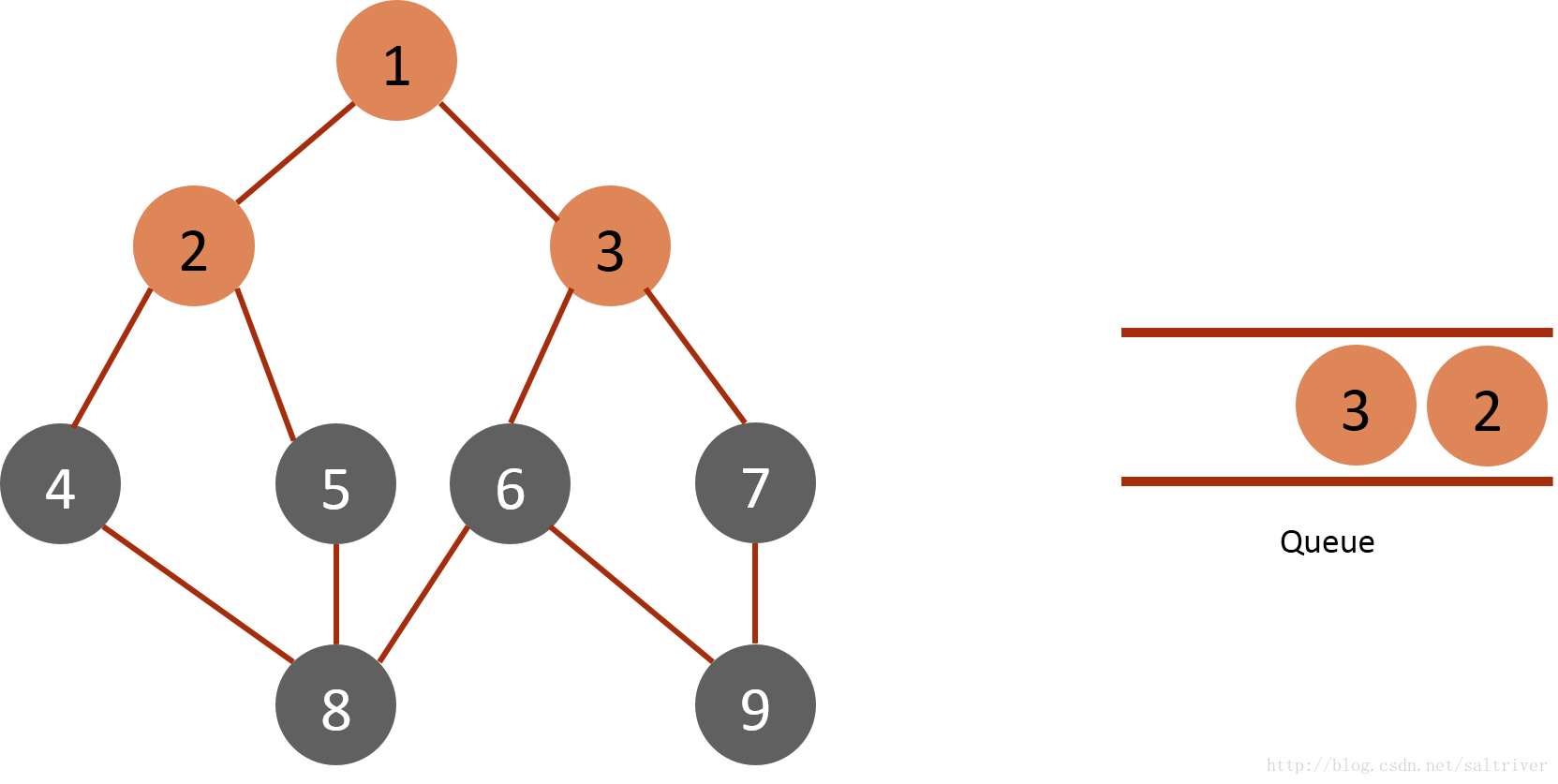
(3) Take node 2 of the queue header from the queue and find nodes 1, 4 and 5 adjacent to node 2. Since node 1 has been traversed, it is excluded; It is traversed and marked as 4,5.
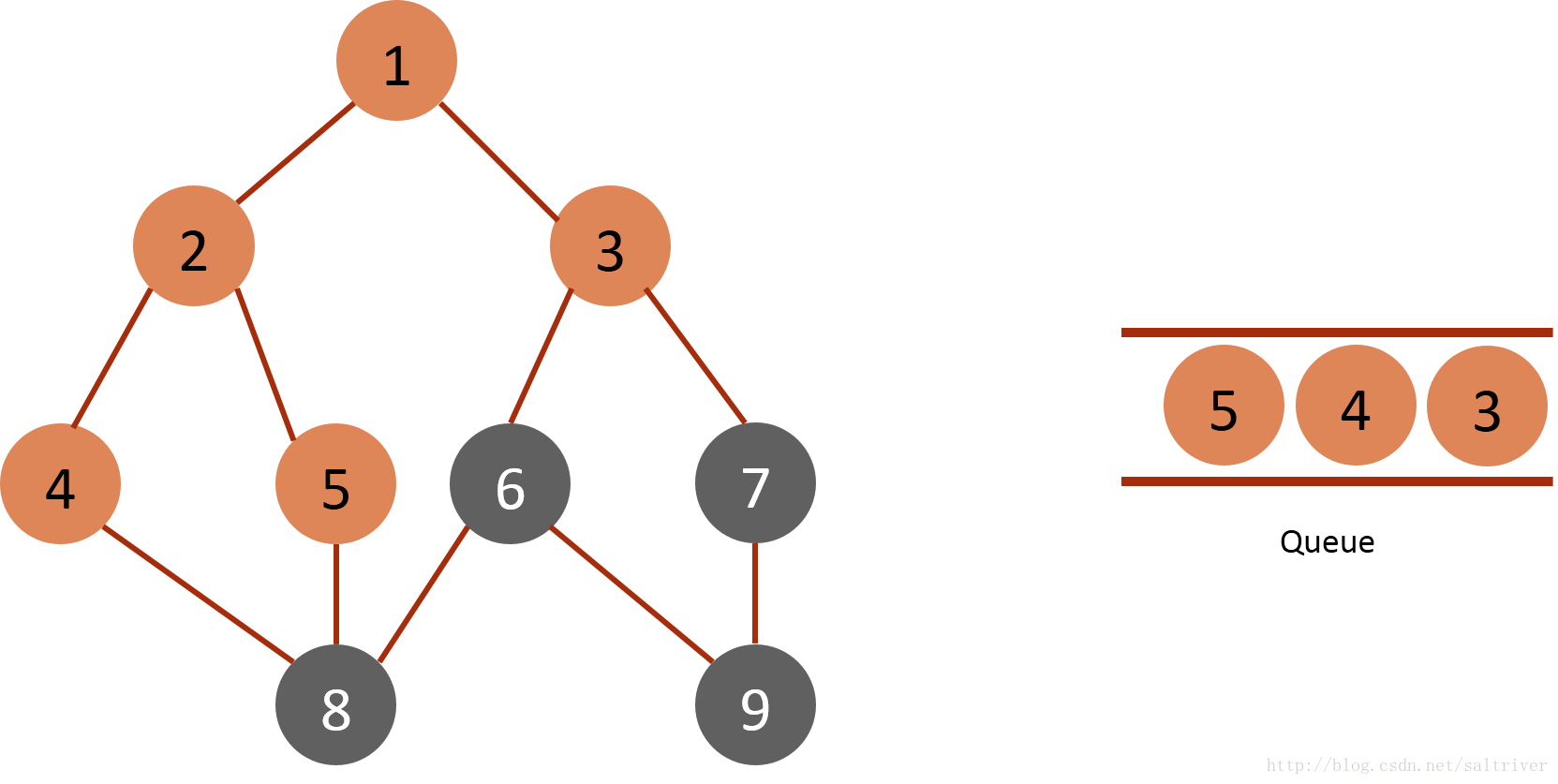
(4) Take the node 3 of the queue header from the queue and find the nodes 1, 6 and 7 adjacent to node 3. Since node 1 has been traversed, it is excluded; Mark 6 and 7 as traversed and put them into the queue.
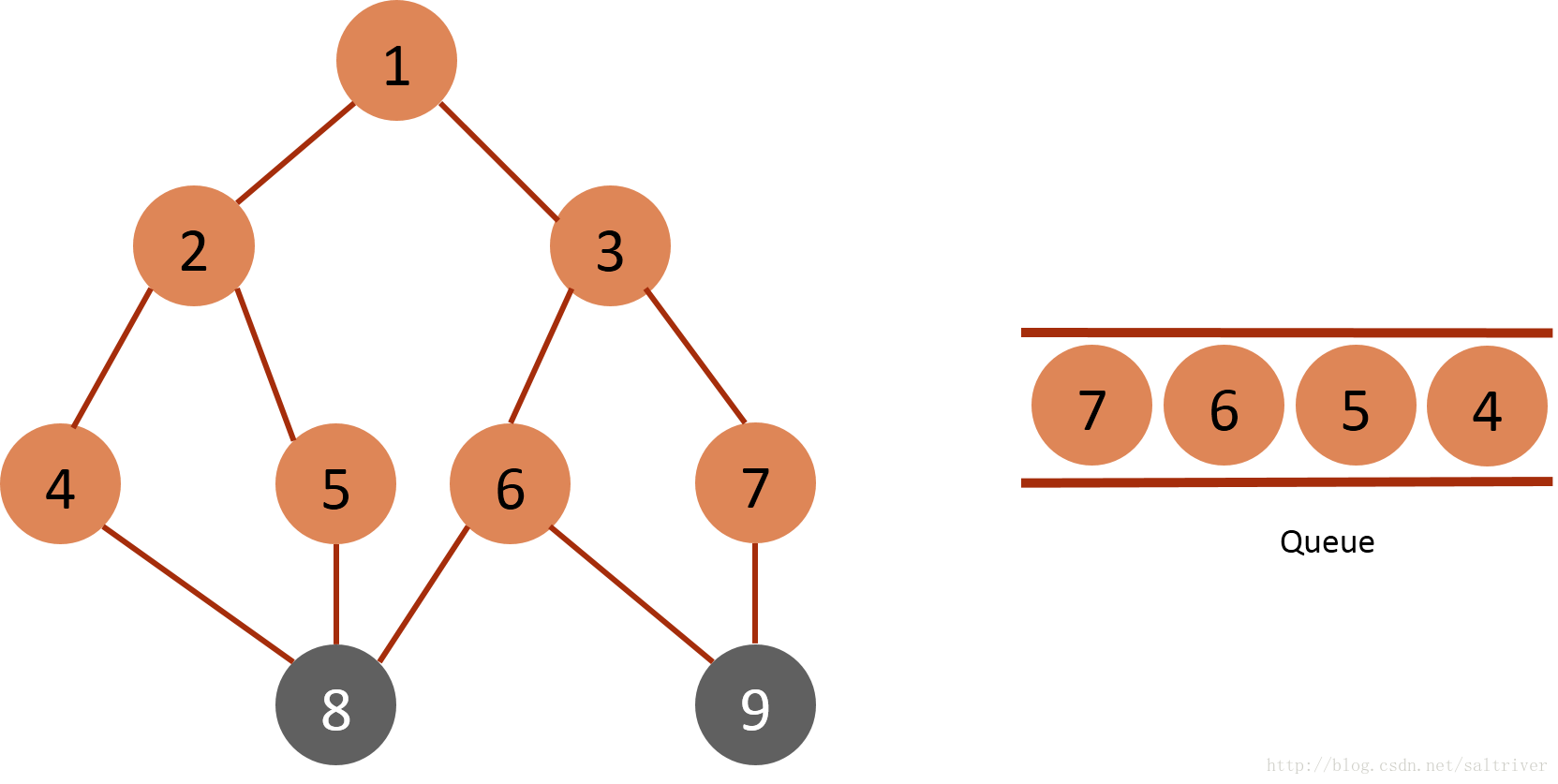
(5) Take out the node 4 of the queue header from the queue, find out the nodes 2, 8 and 2 adjacent to the node 4, which belong to the traversed points and are excluded; Therefore, mark node 8 as traversed and put it into the queue.
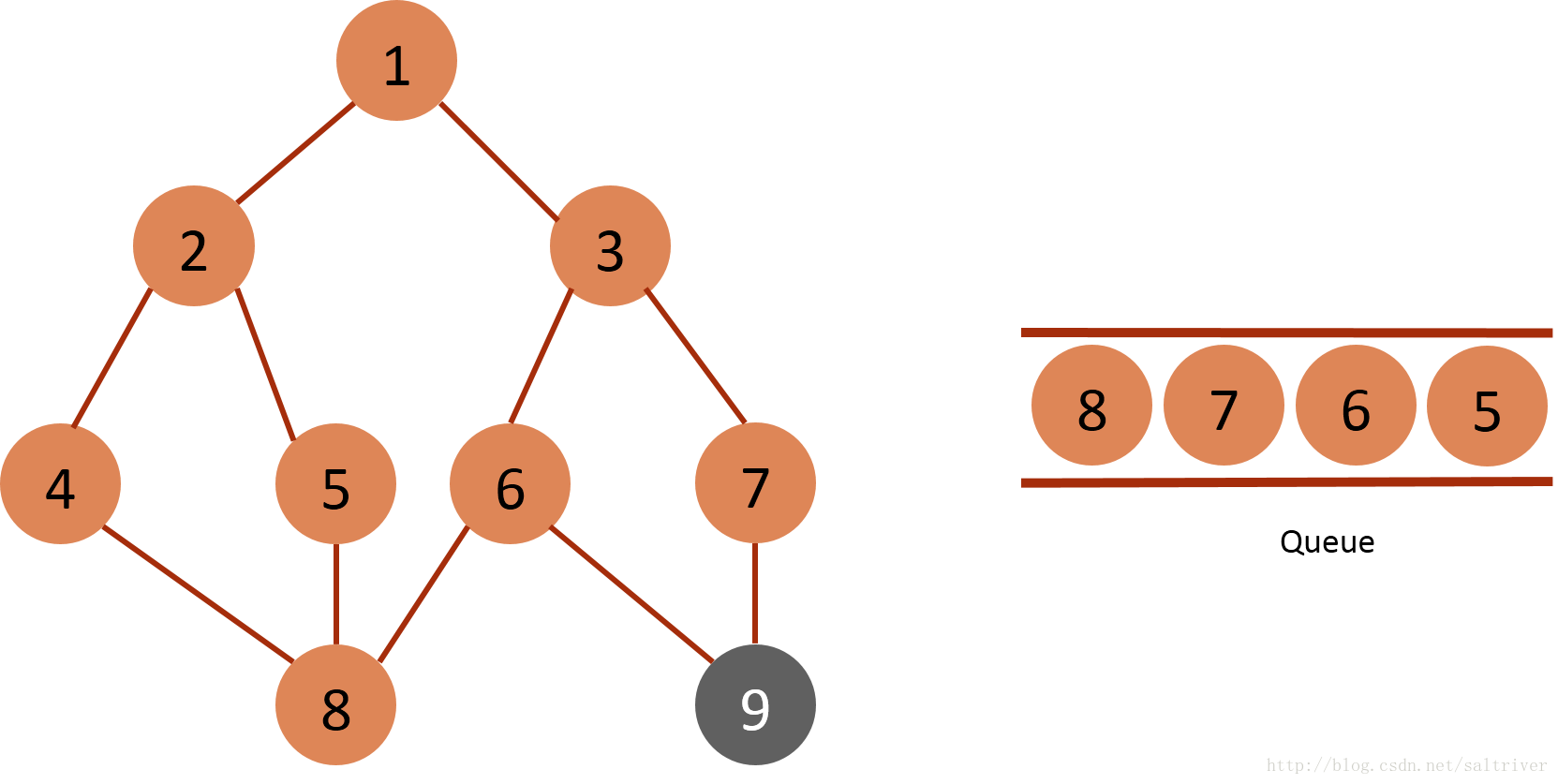
(6) Take out the node 5 of the queue header from the queue, and find out the nodes 2, 8, 2 and 8 adjacent to the node 5, which belong to the traversed points, and do not do the next operation.
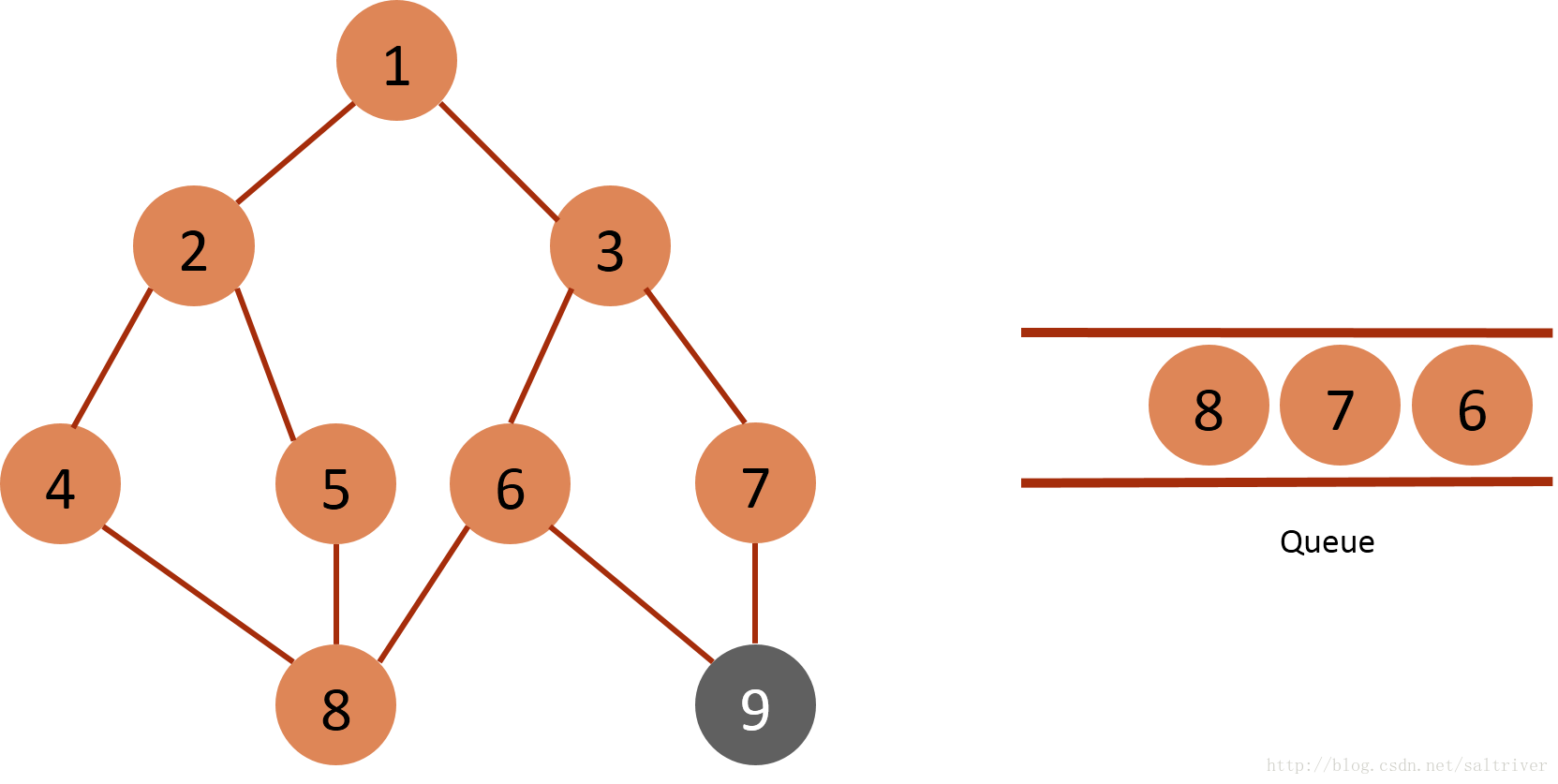
(7) Take out the node 6 of the queue header from the queue, find out that the nodes 3, 8, 9, 3 and 8 adjacent to the node 6 belong to the traversed points, and exclude them; Therefore, mark node 9 as traversed and put it into the queue.
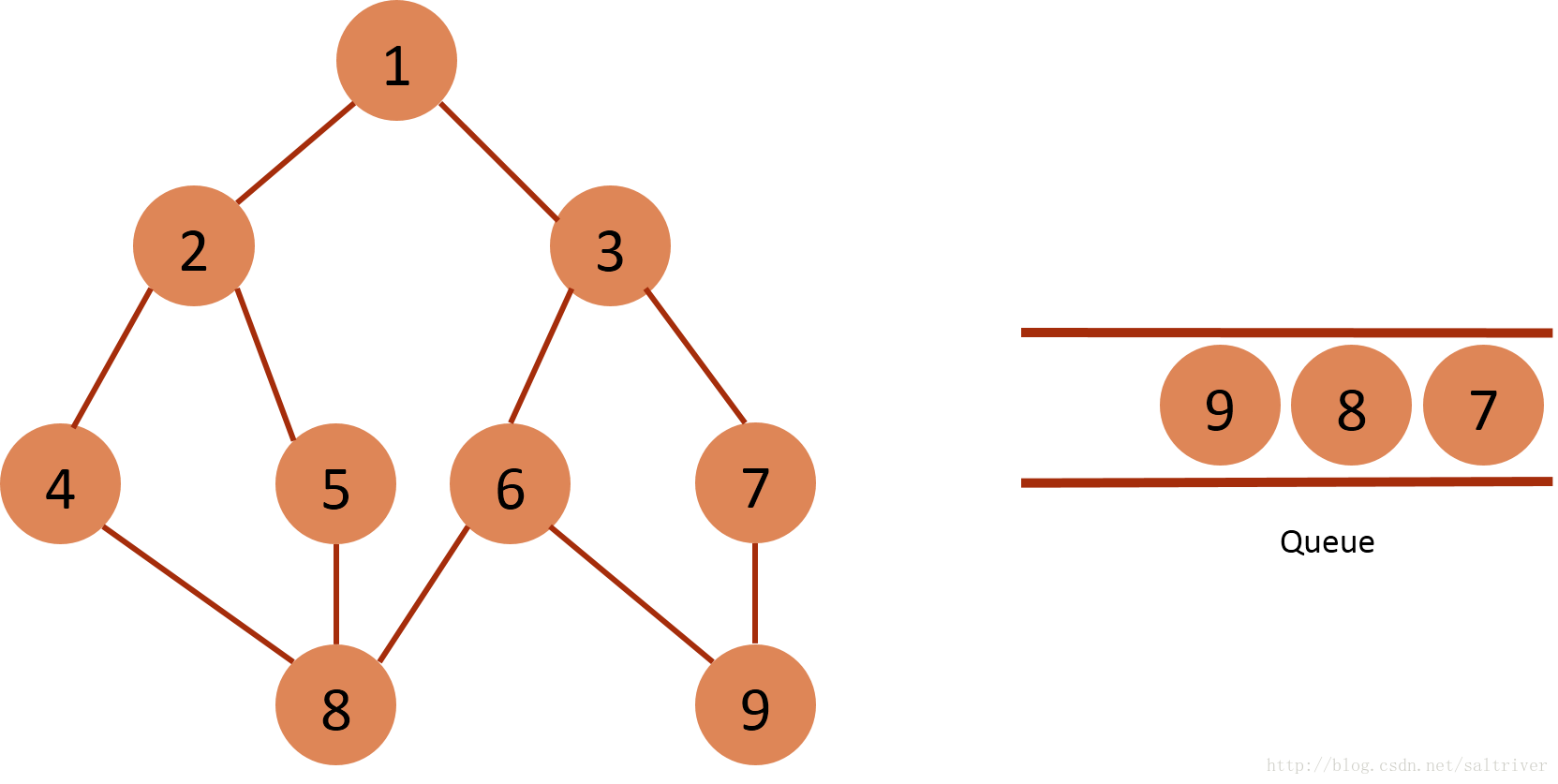
(8) Take out the node 7 of the queue header from the queue, and find out that the nodes 3, 9, 3 and 9 adjacent to the node 7 belong to the traversed points, so do not do the next operation.
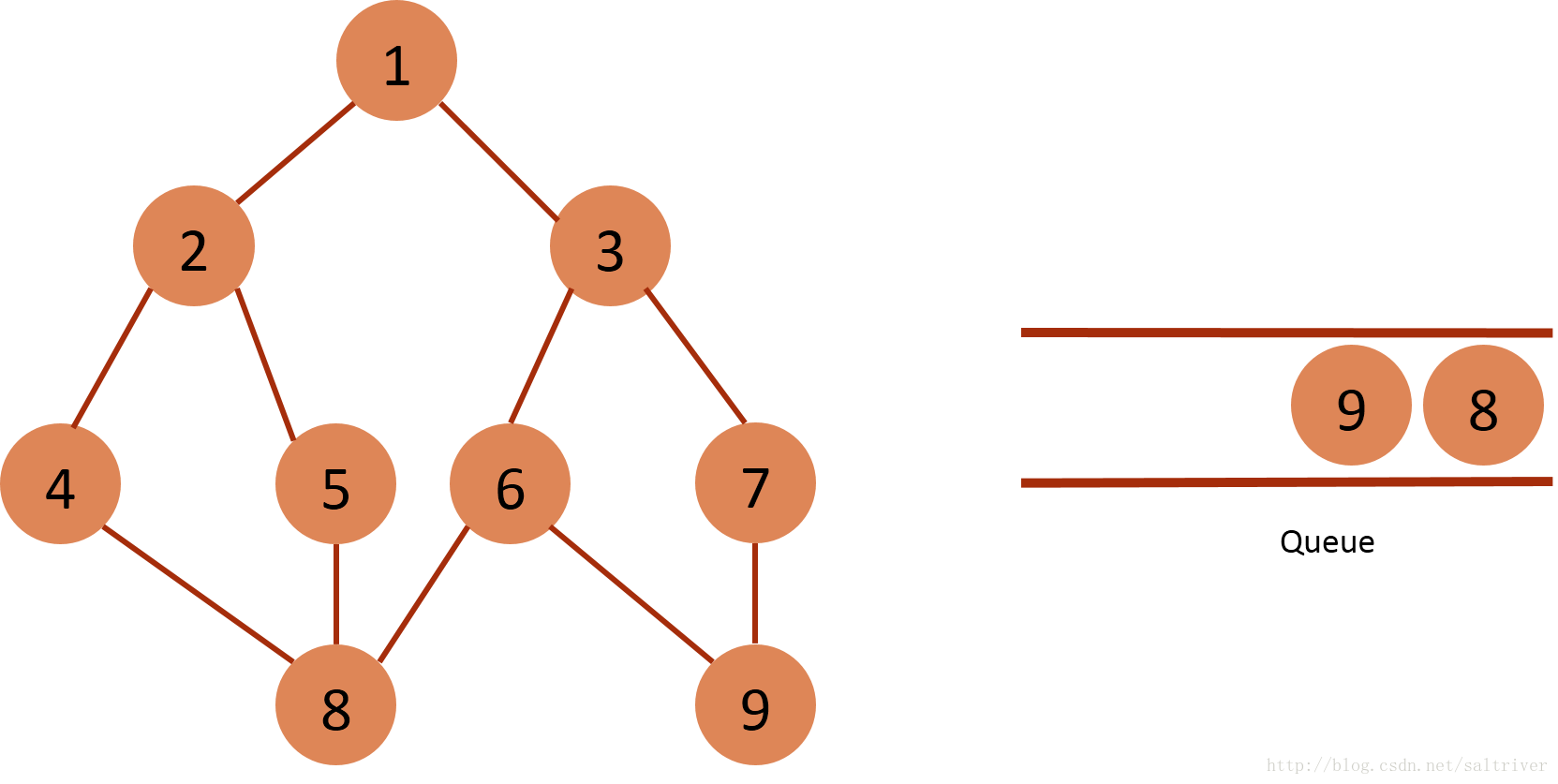
(9) Take out the node 8 of the queue header from the queue, and find out that the nodes 4, 5, 6, 4, 5 and 6 adjacent to the node 8 belong to the traversed points, so do not do the next operation.
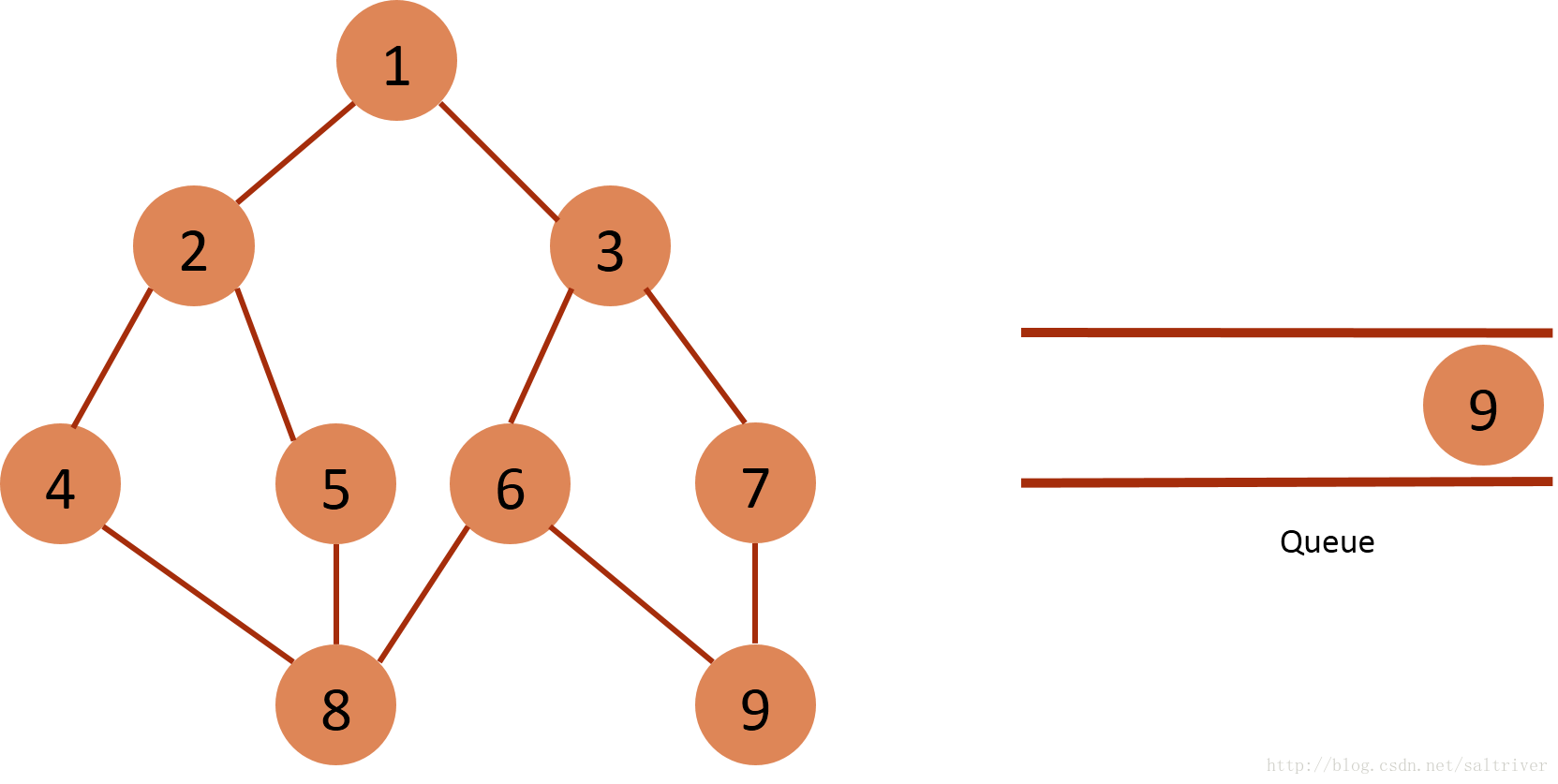
(10) Take out the node 9 of the queue header from the queue, and find out the nodes 6, 7 and 6, 7 adjacent to the node 9, which belong to the traversed points and do not do the next operation.
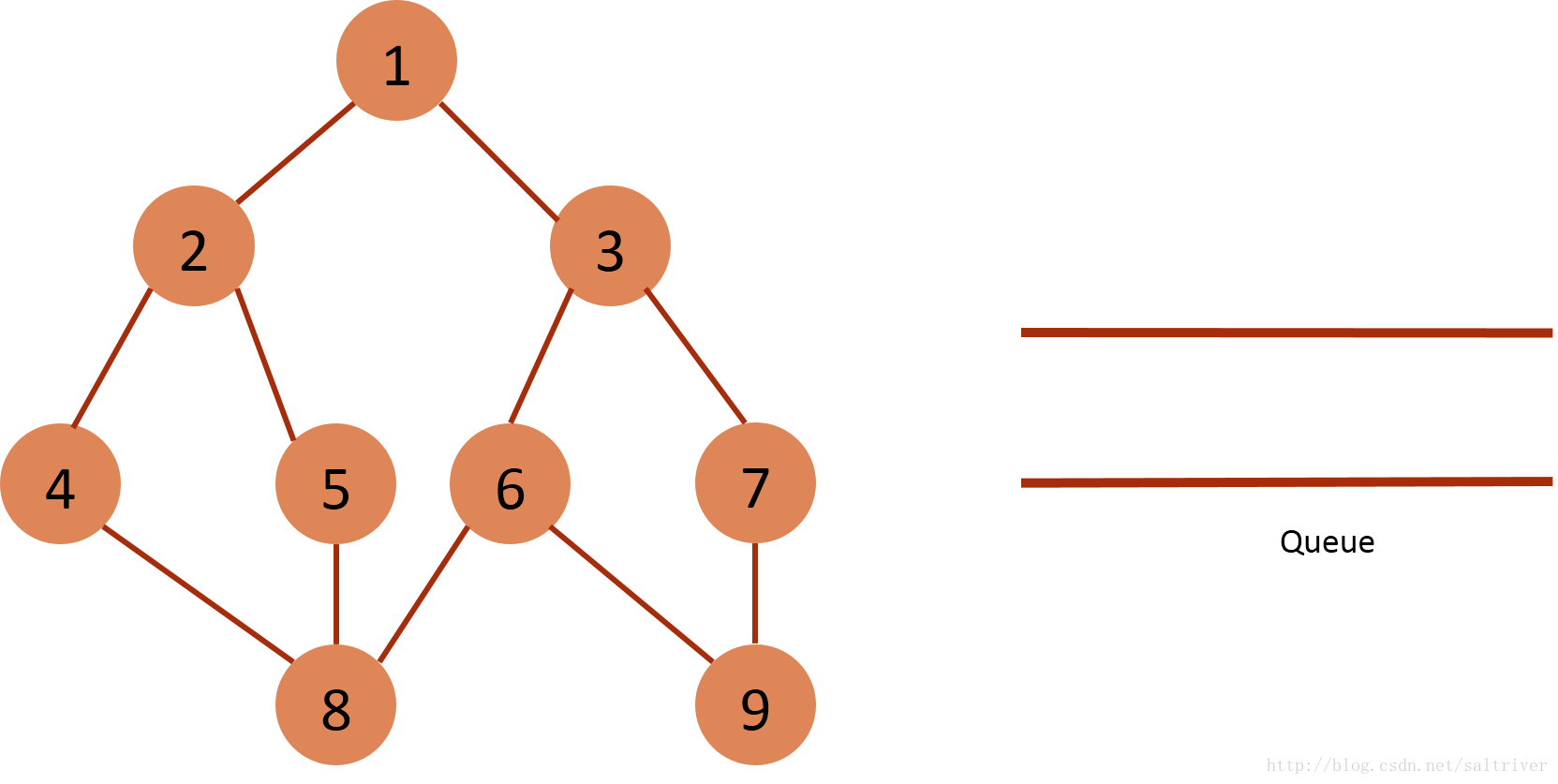
(11) If the queue is empty, BFS traversal ends.
BFS application scenario
- Two scenarios of BFS: sequence traversal and shortest path
- Find the shortest path from a certain point, but the path is not unique. The shortest path is the first one to meet the conditions
- Extensive search
- Words like "shortest" and "least" can be given priority
Implementing BFS in python (tree and graph)
Trees are special graphs
BFS diagram of python implementation
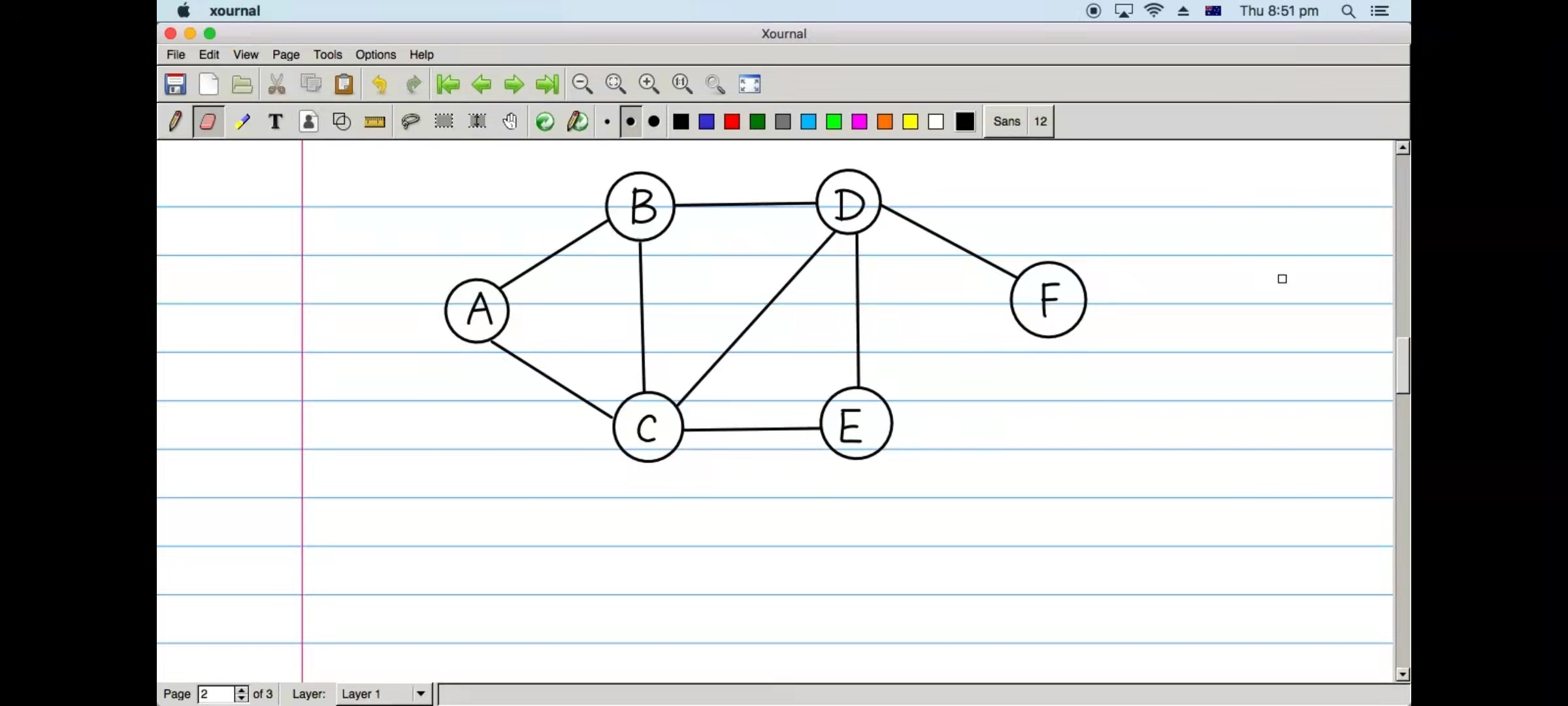
import os
import sys
'''
python realization BFS Graph of
2022-01-15
'''
# Create a dictionary for storing graphs. A dictionary is equivalent to a mapping relationship and is read through key value pairs. It is applicable to only a small number of points in the graph. If there is too much data, it is more appropriate to use python class
graph = {
"A": ["B", "C"],
"B": ["A", "C", "D"],
"C": ["A", "B", "D", "E"],
"D": ["B", "C", "E", "F"],
"E": ["C", "D"],
"F": ["D"]
}
# Start BFS traversal
# Graph is the graph data and s is the starting point of the graph
def BFS(graph, s):
# Create an array as a queue to store points that have not been accessed
queue = []
# Put in starting point
queue.append(s)
# Create a collection to hold the points that have been read in, such as the starting point s
seen = set()
seen.add(s)
# Loop read queue
while (len(queue) > 0):
# Via queue Pop (0) reads the queue head, that is, each point
vertex = queue.pop(0)
# Read the points adjacent to each point
nodes = graph[vertex]
# Weight judgment: cycle to judge whether adjacent points have been read
for w in nodes:
if w not in seen:
queue.append(w)
seen.add(w)
# Output traversal node
print(vertex, end= ' ')
BFS(graph, "A")
'''
# Operation results
A B C D E F
'''
Shortest path of python implementation diagram
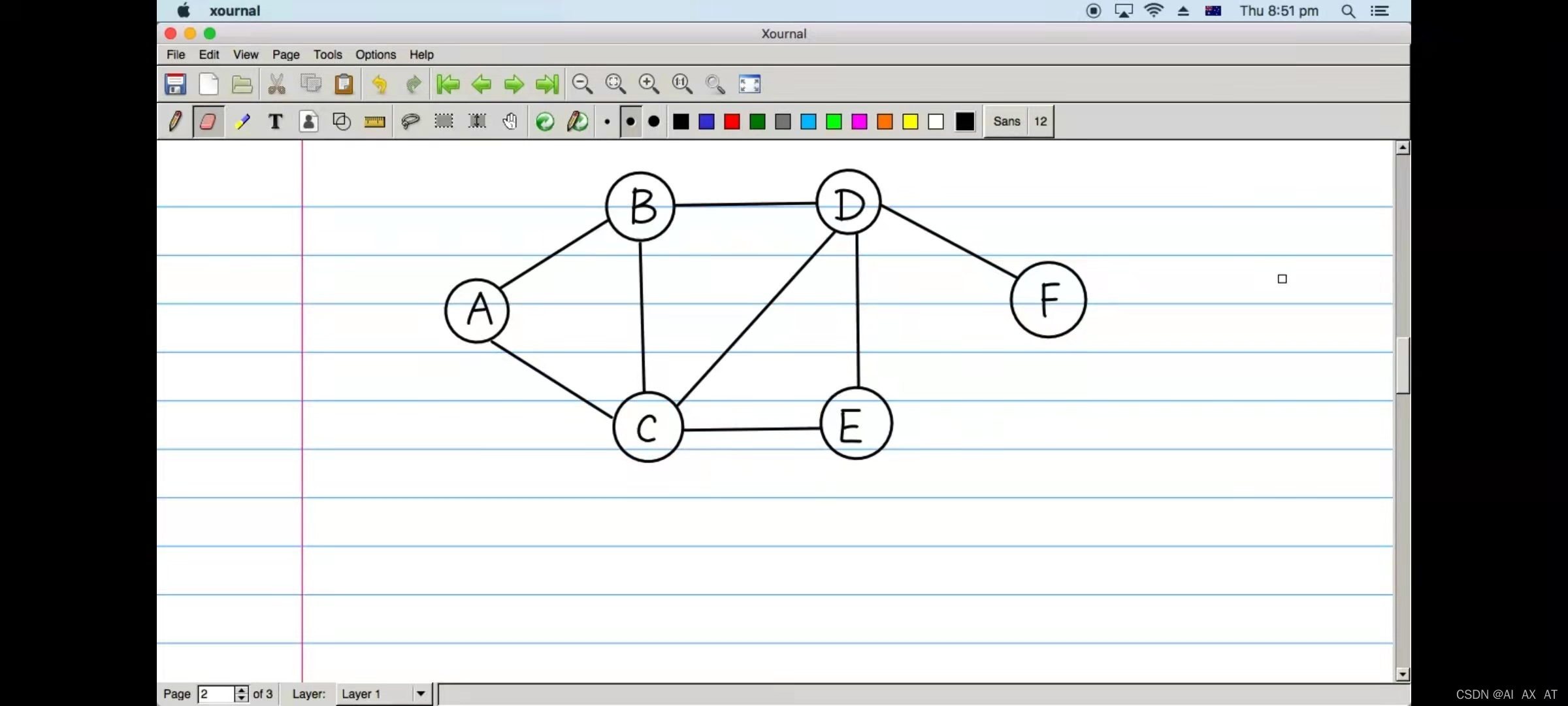
Improved from the above code
import os
import sys
'''
python realization BFS Graph of
2022-01-15
'''
# Create a dictionary for storing graphs. A dictionary is equivalent to a mapping relationship and is read through key value pairs. It is applicable to only a small number of points in the graph. If there is too much data, it is more appropriate to use python class
graph = {
"A": ["B", "C"],
"B": ["A", "C", "D"],
"C": ["A", "B", "D", "E"],
"D": ["B", "C", "E", "F"],
"E": ["C", "D"],
"F": ["D"]
}
# Start BFS traversal
# Graph is the graph data and s is the starting point of the graph
def BFS(graph, s):
# Create an array as a queue to store points that have not been accessed
queue = []
# Put in starting point
queue.append(s)
# Create a collection to hold the points that have been read in, such as the starting point s
seen = set()
seen.add(s)
# Path restore, which corresponds the accessed point to its previous point to form a key value pair, and uses it to complete the output of the shortest path
parent = {s: None}
# Loop read queue
while (len(queue) > 0):
# Via queue Pop (0) reads the queue head, that is, each point
vertex = queue.pop(0)
# Read the points adjacent to each point
nodes = graph[vertex]
# Weight judgment: cycle to judge whether adjacent points have been read
for w in nodes:
if w not in seen:
queue.append(w)
seen.add(w)
parent[w] = vertex
# Output traversal node
# print(vertex, end= ' ')
return parent
parent = BFS(graph, "A")
# Output the shortest path you want
# Set v as the end point
v = 'F'
# Loop find v
while v != None:
print(v, end=' ')
v = parent[v]
'''
# Operation results
F D B A
'''
Implementing BFS tree in python
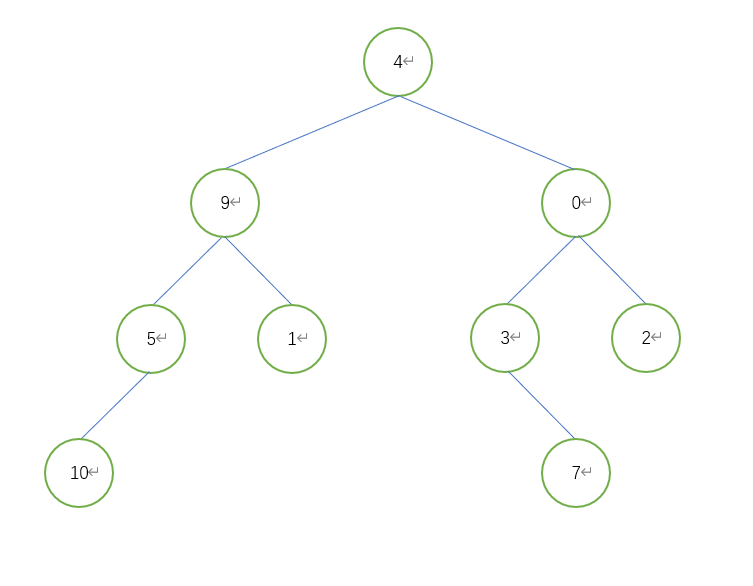
# Define the nodes of a tree
class TreeNode:
def __init__(self, x):
self.val = x # value
self.left = None # Left node
self.right = None # Right node
def level_order_tree(root):
if not root: # A tree has only the root node and returns a null value
return root
queue = []
result = []
queue.append(root) # Queue root node
result.append(root.val) # Add root node value
while len(queue) > 0:
node = queue.pop(0) # Take the head of the line
result.append(node.val)
# Judge left and right subtrees
if node.left: # Add children from the left subtree to the queue
queue.append(node.left)
if node.right: # Add children from the right subtree to the queue
queue.append(node.right)
return result
if __name__ == "__main__":
tree = TreeNode(4)
tree.left = TreeNode(9)
tree.right = TreeNode(0)
tree.left.left = TreeNode(5)
tree.left.right = TreeNode(1)
print(level_order_tree(tree))
# [4, 9, 0, 5, 1, 3, 2, 10, 7]
DFS
What is DFS
- Depth first search (DFS) is an algorithm used to traverse or search trees or graphs. In brief, the process is to go deep into each possible branch path to the point where it can no longer go deep, and each node can only access it once.
- When the edge of node v has been explored or the node does not meet the conditions when searching, the search will be traced back to the starting node of the edge where node v is found. The whole process repeats until all nodes are accessed.
- For the same tree or graph, the DFS order is not necessarily unique.
- Depth first search is realized by stack, which has the characteristics of first in and last out.
DFS working process and principle
DFS working process and principle
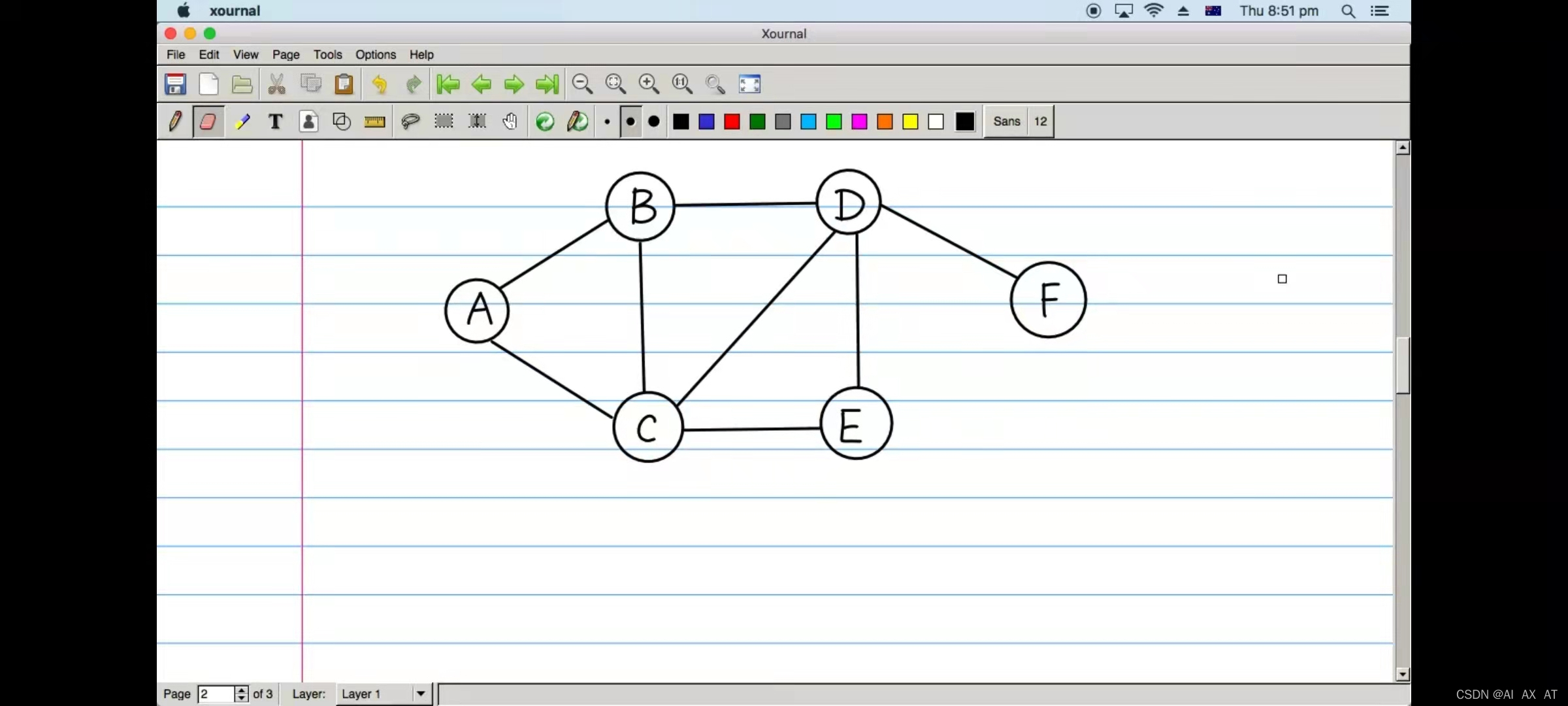
Please don't forget that DFS order is not necessarily unique.
- Take A as the starting node and access A. the adjacent points connected with A are B and C.
- At this point, you can access B and C. which one you access depends on the order in which you press the stack.
- Visit B, and the adjacent points connected to B are C and D.
- Access D, and the adjacent points connected to D are E and F.
- Access F, f has no adjacency point, and the nearest adjacency point D when the original path returns.
- The adjacency point e connected with D has not been accessed. Access e, and the adjacency points connected with E are C and D.
- Access C. the adjacency points of C include A, B, D and E. all have been visited. The original path returns to D. at this time, the adjacency points of d have been visited. The original path returns to B and then to A.
DFS application scenario
- Seeking subsequence and subset
- Find all possible solutions and assemble the results layer by layer (not much different from the first one)
Implementing DFS with python
DFS diagram implemented in python
import os
import sys
'''
python realization DFS Graph of
2022-01-15
'''
# Create a dictionary for storing graphs. A dictionary is equivalent to a mapping relationship and is read through key value pairs. It is applicable to only a small number of points in the graph. If there is too much data, it is more appropriate to use python class
graph = {
"A": ["B", "C"],
"B": ["A", "C", "D"],
"C": ["A", "B", "D", "E"],
"D": ["B", "C", "E", "F"],
"E": ["C", "D"],
"F": ["D"]
}
# Start DFS traversal
# Graph is the graph data and s is the starting point of the graph
def BFS(graph, s):
# Create an array as a stack to store points that have not been accessed
stack = []
# Put in starting point
stack.append(s)
# Create a collection to hold the points that have been read in, such as the starting point s
seen = set()
seen.add(s)
# Cyclic read stack
while (len(stack) > 0):
# Via queue Pop() reads the last on the stack
vertex = stack.pop()
# Read the points adjacent to each point
nodes = graph[vertex]
# Weight judgment: cycle to judge whether adjacent points have been read
for w in nodes:
if w not in seen:
stack.append(w)
seen.add(w)
# Output traversal node
print(vertex, end= ' ')
BFS(graph, "A")
'''
# Operation results
A C E D F B
'''
Implementing DFS tree in python
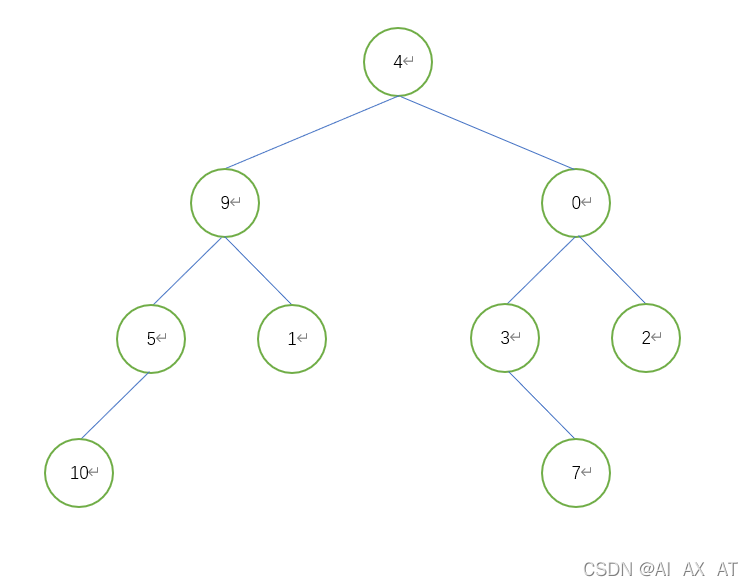
# Create tree node class val: value, left: left subtree, right: right subtree
class TreeNode:
def __init__(self, value):
self.val = value
self.left = None
self.right = None
# Deep search traversal binary tree
def DFS(root):
# Create a storage result array
res = []
# Create a stack. The stack has the characteristics of last in first out. First put it into the root node
stack = [root]
# Loop stack
while stack:
# Take out the last element of the stack
currentNode = stack.pop()
# Get the value of the element
res.append(currentNode.val)
# Include right subtree
if currentNode.right:
# Add right subtree to stack
stack.append(currentNode.right)
# Whether to include left subtree
if currentNode.left:
# Add left subtree to stack
stack.append(currentNode.left)
# Return results
return res
if __name__ == "__main__":
tree = TreeNode(4) # Add root node
tree.left = TreeNode(9) # Add root left subtree
tree.right = TreeNode(0) # Add root right subtree, and so on
tree.left.left = TreeNode(5)
tree.left.right = TreeNode(1)
tree.right.left = TreeNode(3)
tree.right.right = TreeNode(2)
tree.left.left.left = TreeNode(10)
tree.right.left.right = TreeNode(7)
print(DFS(tree))
# [4, 9, 5, 10, 1, 0, 3, 7, 2]
'''
Operation results:
[4, 9, 5, 10, 1, 0, 3, 7, 2]
'''
When to use deep search and wide search
- BFS is used to search the solution of the shortest path, which is more appropriate, such as the solution with the least steps and the solution with the least exchange times. Because the solution encountered in the process of BFS search must be the closest to the root, the solution encountered must be the optimal solution. At this time, the search algorithm can be terminated. It is not appropriate to use DFS at this time, because the solution searched by DFS is not necessarily the closest to the root. Only after the global search is completed can we find the nearest solution to the root from all solutions. (of course, the deficiency of DFS can be made up by using iterative deepening search ID-DFS).
- In terms of space, DFS has advantages. DFS does not need to save the state in the search process, while BFS needs to save the searched state in the search process, and generally a queue is needed to record.
- DFS is suitable for searching all solutions, because to search all solutions, it is useless to encounter the solution closest to the root in the BFS search process. You must traverse the entire search tree, and DFS search will also search all solutions. However, compared with DFS, DFS does not need to record too much information, so DFS is obviously more suitable for searching all solutions.
python implements the traversal of the tree before, during and after the sequence
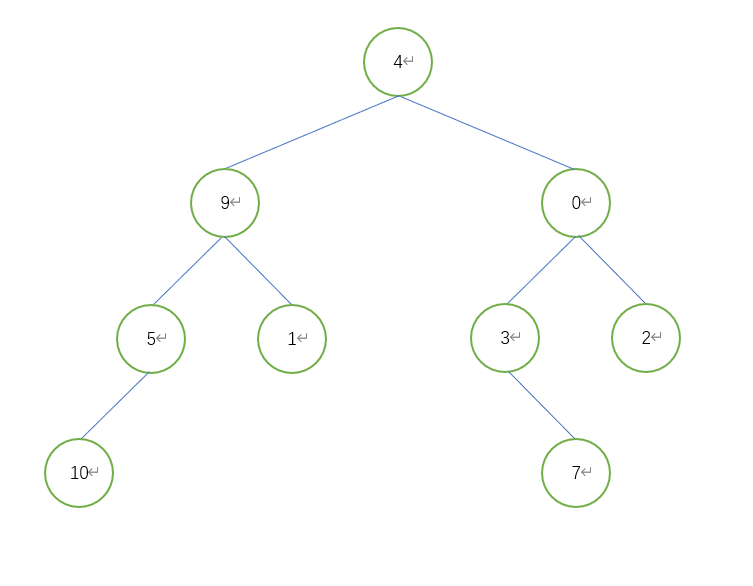
Preorder traversal
# Define the nodes of a tree
class TreeNode:
def __init__(self, x):
self.val = x # value
self.left = None # Left node
self.right = None # Right node
# Preorder traversal. lis is the passed in list type parameter. In order to get a traversal result of list recursively
def preorder(root, result):
result.append(root.val) # Add root node value
if root.left:
preorder(root.left, result) # Recursive search for left subtree
if root.right:
preorder(root.right, result) # Recursive search for right subtree
return result
if __name__ == "__main__":
tree = TreeNode(4) # Add root node
tree.left = TreeNode(9) # Add root left subtree
tree.right = TreeNode(0) # Add root right subtree, and so on
tree.left.left = TreeNode(5)
tree.left.right = TreeNode(1)
tree.right.left = TreeNode(3)
tree.right.right = TreeNode(2)
tree.left.left.left = TreeNode(10)
tree.right.left.right = TreeNode(7)
print(preorder(tree, []))
# [4, 9, 5, 10, 1, 0, 3, 7, 2]
Middle order traversal
# Define the nodes of a tree
class TreeNode:
def __init__(self, x):
self.val = x # value
self.left = None # Left node
self.right = None # Right node
# Medium order traversal. lis is the passed in list parameter. In order to get a traversal result of list recursively
def infix_order(root, result):
if root.left:
infix_order(root.left, result)
result.append(root.val)
if root.right:
infix_order(root.right, result)
return result
if __name__ == "__main__":
tree = TreeNode(4) # Add root node
tree.left = TreeNode(9) # Add root left subtree
tree.right = TreeNode(0) # Add root right subtree, and so on
tree.left.left = TreeNode(5)
tree.left.right = TreeNode(1)
tree.right.left = TreeNode(3)
tree.right.right = TreeNode(2)
tree.left.left.left = TreeNode(10)
tree.right.left.right = TreeNode(7)
print(infix_order(tree, []))
# [10, 5, 9, 1, 4, 3, 7, 0, 2]
Postorder traversal
# Define the nodes of a tree
class TreeNode:
def __init__(self, x):
self.val = x # value
self.left = None # Left node
self.right = None # Right node
# Post order traversal. Result is the passed in list type parameter. In order to get a traversal list result recursively
def epilogue(root, result):
if root.left:
epilogue(root.left, result)
if root.right:
epilogue(root.right, result)
result.append(root.val)
return result
if __name__ == "__main__":
tree = TreeNode(4) # Add root node
tree.left = TreeNode(9) # Add root left subtree
tree.right = TreeNode(0) # Add root right subtree, and so on
tree.left.left = TreeNode(5)
tree.left.right = TreeNode(1)
tree.right.left = TreeNode(3)
tree.right.right = TreeNode(2)
tree.left.left.left = TreeNode(10)
tree.right.left.right = TreeNode(7)
print(epilogue(tree, []))
# [10, 5, 1, 9, 7, 3, 2, 0, 4]