This article is reproduced from: https://zhuanlan.zhihu.com/p/36233589
Record learning only~
summary
This chapter is just a summary of the routine operation of pytorch. It's good to have an impression in your mind. You know that there is such a thing. You can look at it in detail when you need it. In addition, you still need to use it in practice.
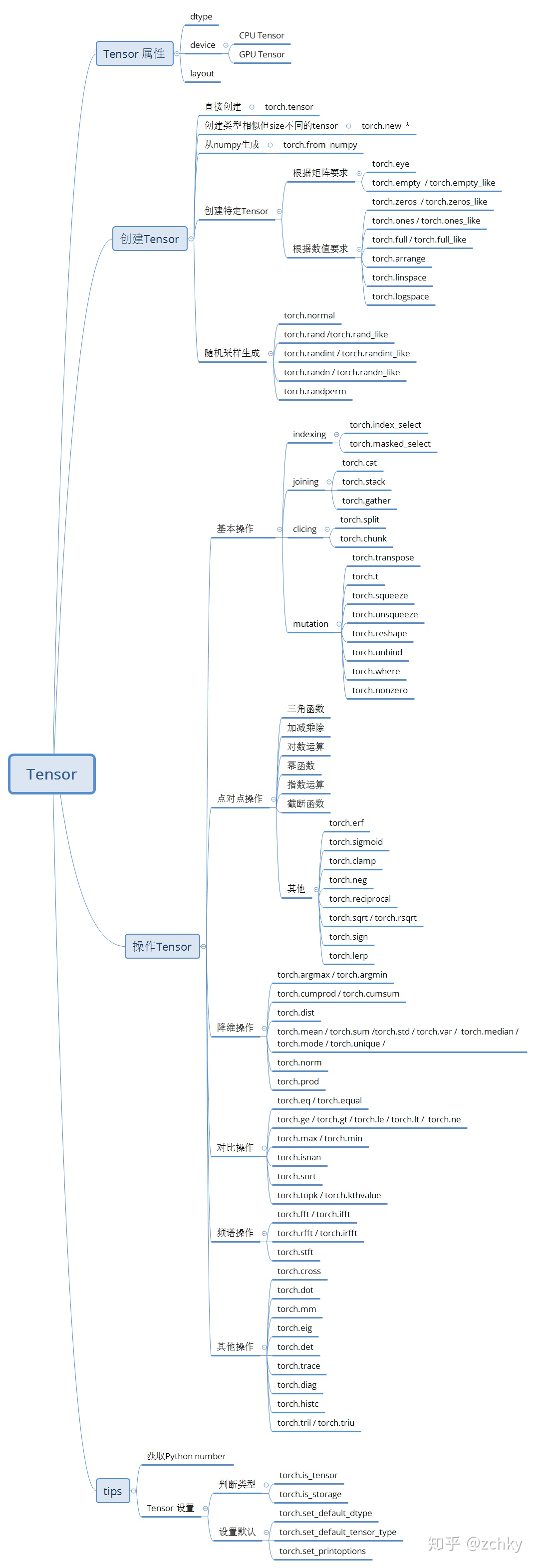
elaboration
Tensor attributes:
There are three classes in tensor attributes: torch dtype, torch. Device, and torch layout
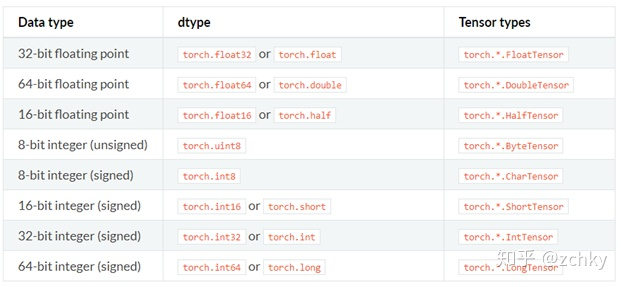
Among them, torch dtype is the display torch There are eight complete data types in the list of. Tenstor
Torch.device is the performance torch The class of the device type assigned to tensor, which is divided into 'cpu' and 'CUDA'. If the device serial number is not displayed, it means that this tensor is assigned to the current device. For example, 'CUDA' is equivalent to 'CUDA': X, X is torch cuda. current _ Device() return value
We can use tensor Device to obtain its attributes, and the device can be allocated by character or character + sequence number
By string:
>>> torch.device('cuda:0')
device(type='cuda', index=0)
>>> torch.device('cpu')
device(type='cpu')
>>> torch.device('cuda') # Current equipment
device(type='cuda')
By string and device serial number:
>>> torch.device('cuda', 0)
device(type='cuda', index=0)
>>> torch.device('cpu', 0)
device(type='cpu', index=0)
In addition, the conversion between cpu and cuda device is realized by 'to':
device_cpu = torch.device("cuda") #Declare cuda device
device_cuda = torch.device('cuda') #Device cpu device
data = torch.Tensor([1])
data.to(device_cpu) #Convert data to cpu format
data.to(device_cuda) #Convert data to cuda format
torch.layout is the performance torch Tensor memory distribution class. Currently, it only supports torch strided
Create Tensor
Create directly
torch.tensor(data, dtype=None, device=None,requires_grad=False) data - Can be list, tuple, numpy array, scalar Or other types dtype - You can return what you want tensor type device - You can specify the device to return requires_grad - You can specify whether to record the chart. The default value is False
It should be noted that torch Tensor will always copy data. If you want to avoid copying, you can make torch Tensor. Detach(), if you get data from numpy, you can use torch from_numpy(), note from_numpy() is shared memory
>>> torch.tensor([[0.1, 1.2], [2.2, 3.1], [4.9, 5.2]])
tensor([[ 0.1000, 1.2000],
[ 2.2000, 3.1000],
[ 4.9000, 5.2000]])
>>> torch.tensor([0, 1]) # Type inference on data
tensor([ 0, 1])
>>> torch.tensor([[0.11111, 0.222222, 0.3333333]],
dtype=torch.float64,
device=torch.device('cuda:0')) # creates a torch.cuda.DoubleTensor
tensor([[ 0.1111, 0.2222, 0.3333]], dtype=torch.float64, device='cuda:0')
>>> torch.tensor(3.14159) # Create a scalar (zero-dimensional tensor)
tensor(3.1416)
>>> torch.tensor([]) # Create an empty tensor (of size (0,))
tensor([])
Get data from numpy
torch.from_numpy(ndarry)
Note: the generated and returned tensor will share data with Darry, and any operation on tensor will affect Darry,
vice versa
>>> a = numpy.array([1, 2, 3]) >>> t = torch.from_numpy(a) >>> t tensor([ 1, 2, 3]) >>> t[0] = -1 >>> a array([-1, 2, 3])
Create a specific tensor
- According to the numerical requirements:
torch.zeros(*sizes, out=None, ..)# Returns a zero matrix of sizes torch.zeros_like(input, ..) # Returns a zero matrix of the same size as input torch.ones(*sizes, out=None, ..) #f returns the identity matrix of sizes torch.ones_like(input, ..) #Returns the identity matrix with the same size as input torch.full(size, fill_value, ...) #The returned size is sizes and the unit value is fill_value matrix torch.full_like(input, fill_value, ...) Return and input identical size,Unit value is fill_value Matrix of torch.arange(start=0, end, step=1, ...) #Returns the 1-d tensor from start to end in step torch.linspace(start, end, steps=100, ...) #Returns the 1-d tensor from start to end with the number of interpolated steps in the interval torch.logspace(start, end, steps=100, ...) #Returns the 1-d tensor, and the steps from 10^start to 10^end are logarithmic intervals
- According to the matrix requirements:
torch.eye(n, m=None, out=None,...) #Returns the identity diagonal matrix of 2-D torch.empty(*sizes, out=None, ...) #Returns a tensor of sizes filled with uninitialized values torch.empty_like(input, ...) # Returns a tensor with the same size as input and filled with uninitialized values
Random use generation:
torch.normal(mean, std, out=None) torch.rand(*size, out=None, dtype=None, ...) #Returns a random number evenly distributed between [0,1] torch.rand_like(input, dtype=None, ...) #Returns a tensor of the same size as the input, and fills in evenly distributed random values torch.randint(low=0, high, size,...) #Returns an integer random value between uniformly distributed [low,high] torch.randint_like(input, low=0, high, dtype=None, ...) # torch.randn(*sizes, out=None, ...) #The mean value of size is 0, and the variance of size is normal torch.randn_like(input, dtype=None, ...) torch.randperm(n, out=None, dtype=torch.int64) # Returns the random arrangement of sequences from 0 to n-1
Operate Tensor
Joining ops
torch.cat(seq,dim=0,out=None) # Connect the tensors in seq along the dim. All tensors must have the same size or empty, and the opposite operation is torch Split () and torch chunk() torch.stack(seq, dim=0, out=None) #As above, add a new dimension to splice, such as #Note: Cat and The difference between stack and cat is that cat will increase the value of the existing dimension, which can be understood as continuation. Stack will add a new dimension, which can be understood as superposition. #cat is cumulative splicing according to the specified dimension (default 0): 50 1 * 3 * 7 * 7 -- "50 * 3 * 7 * 7 stack is a new one-dimensional splicing, which becomes 50 * 1 * 3 * 7 * 7 >>> a=torch.Tensor([1,2,3]) #One dimensional tensor, dimension 3 >>> torch.stack((a,a)).size() torch.size(2,3) # Add one dimension and change to two dimensions (2, 3) >>> torch.cat((a,a)).size() torch.size(6) #The dimension remains unchanged and the original dimension is superimposed
torch.gather(input, dim, index, out=None) #Returns the new tensor collected along the dim >> t = torch.Tensor([[1,2],[3,4]]) >> index = torch.LongTensor([[0,0],[1,0]]) >> torch.gather(t, 0, index) #Since dim=0, the result is | t[index[0, 0] 0] t[index[0, 1] 1] | | t[index[1, 0] 0] t[index[1, 1] 1] | For 3-D In terms of tensor, it can be used as out[i][j][k] = input[index[i][j][k]][j][k] # if dim == 0 out[i][j][k] = input[i][index[i][j][k]][k] # if dim == 1 out[i][j][k] = input[i][j][index[i][j][k]] # if dim == 2
Clipping Ops
torch.split(tensor, split_size_or_sections, dim=0) #Split the tensor into corresponding blocks torch.chunk(tensor, chunks, dim=0) #take tensor Split into corresponding blocks. The last block will be smaller if it cannot be divided# #Note: the difference between split and chunk lies in: split of split_size_or_sections Represents the data size in each chunk, chunks Indicates the number of chunks >>> a = torch.Tensor([1,2,3]) >>> torch.split(a,1) (tensor([1.]), tensor([2.]), tensor([3.])) >>> torch.chunk(a,1) (tensor([ 1., 2., 3.]),)
Indexing ops
torch.index_select(input, dim, index, out=None) #Returns the specified tensor along the dim. The index should be of type longTensor and does not share memory
torch.masked_select(input, mask, out=None) #Return the value of input according to mask, which is 1-D tensor Mask is ByteTensor, true is returned, false is not returned, and the return value does not share memory
>>> x = torch.randn(3, 4)
>>> x
tensor([[ 0.3552, -2.3825, -0.8297, 0.3477],
[-1.2035, 1.2252, 0.5002, 0.6248],
[ 0.1307, -2.0608, 0.1244, 2.0139]])
>>> mask = x.ge(0.5)
>>> mask
tensor([[ 0, 0, 0, 0],
[ 0, 1, 1, 1],
[ 0, 0, 0, 1]], dtype=torch.uint8)
>>> torch.masked_select(x, mask)
tensor([ 1.2252, 0.5002, 0.6248, 2.0139])
Deformation Ops
torch.transpose(input, dim0, dim1, out=None) #Returns the tensor after the exchange of dim0 and dim1
torch.t(input, out=None) #Designed for transpose of 2D matrix, it is a convenient function of transpose
torch.squeeze(input, dim, out=None) #All dimensions with size 1 are removed by default. When dim is specified, dimensions with size 1 are removed The returned tensor will share storage space with the input, so any change will affect the other
torch.unsqueeze(input, dim, out=None) #Expand the size of input, for example, A x B becomes 1 x A x B
torch.reshape(input, shape) #Return the tensor whose size is shape and has the same value. Note the expression of shape=(-1,), - 1 means arbitrary.
#Note reshape(-1,)
>>> a=torch.Tensor([1,2,3,4,5]) #a.size is torch size(5)
>>> b=a.reshape(1,-1) #Indicates that the first dimension is 1 and the second dimension is filled with the size of a
>>> b.size()
torch.size([1,5])
torch.where(condition,x,y) #The values of x and y are determined according to the value of condition. true returns the value of x and false returns the value of y to form a new tensor
torch.unbind(tensor, dim=0) #Return tuple to unbind the specified dim, which is equivalent to splitting according to the specified dim
>>> a=torch.Tensor([[1,2,3],[2,3,4]])
>>> torch.unbind(a,dim=0)
(torch([1,2,3]),torch([2,3,4])) # Divide one (2,3) into two (3)
torch.nonzero(input, out=None) # Returns the index of non-zero value. Each row is an index value of non-zero value
>>> torch.nonzero(torch.tensor([1, 1, 1, 0, 1]))
tensor([[ 0],
[ 1],
[ 2],
[ 4]])
>>> torch.nonzero(torch.tensor([[0.6, 0.0, 0.0, 0.0],
[0.0, 0.4, 0.0, 0.0],
[0.0, 0.0, 1.2, 0.0],
[0.0, 0.0, 0.0,-0.4]]))
tensor([[ 0, 0],
[ 1, 1],
[ 2, 2],
[ 3, 3]])
Mathematical operation
Point to point operation
trigonometric function
torch.abs(input, out=None) torch.acos(input, out=None) torch.asin(input, out=None) torch.atan(input, out=None) torch.atan2(input, inpu2, out=None) torch.cos(input, out=None) torch.cosh(input, out=None) torch.sin(input, out=None) torch.sinh(input, out=None) torch.tan(input, out=None) torch.tanh(input, out=None)
Basic operation, addition, subtraction, multiplication and division
Torch.add(input, value, out=None)
.add(input, value=1, other, out=None)
.addcdiv(tensor, value=1, tensor1, tensor2, out=None)
.addcmul(tensor, value=1, tensor1, tensor2, out=None)
torch.div(input, value, out=None)
.div(input, other, out=None)
torch.mul(input, value, out=None)
.mul(input, other, out=None)
Logarithmic operation
torch.log(input, out=None) # y_i=log_e(x_i) torch.log1p(input, out=None) #y_i=log_e(x_i+1) torch.log2(input, out=None) #y_i=log_2(x_i) torch.log10(input,out=None) #y_i=log_10(x_i)
power function
torch.pow(input, exponent, out=None) # y_i=input^(exponent)
exponential function
torch.exp(tensor, out=None) #y_i=e^(x_i) torch.expm1(tensor, out=None) #y_i=e^(x_i) -1
Truncation Functions
torch.ceil(input, out=None) #Returns the smallest integer obtained in the positive direction torch.floor(input, out=None) #Returns the maximum integer obtained in the negative direction torch.round(input, out=None) #Returns the nearest adjacent integer, rounded torch.trunc(input, out=None) #Returns an integer partial value torch.frac(tensor, out=None) #Returns a decimal value torch.fmod(input, divisor, out=None) #Returns the remainder of input / division torch.remainder(input, divisor, out=None) #ditto
Other operations
torch.erf(tensor, out=None) torch.erfinv(tensor, out=None) torch.sigmoid(input, out=None) torch.clamp(input, min, max out=None) #If input < min is returned, min is returned; if input > max, Max is returned; otherwise, input is returned torch.neg(input, out=None) #out_i=-1*(input) torch.reciprocal(input, out=None) # out_i= 1/input_i torch.sqrt(input, out=None) # out_i=sqrt(input_i) torch.rsqrt(input, out=None) #out_i=1/(sqrt(input_i)) torch.sign(input, out=None) #out_i=sin(input_i) greater than 0 is 1, less than 0 is - 1 torch.lerp(start, end, weight, out=None)
Dimensionality reduction operation
torch.argmax(input, dim=None, keepdim=False) #Returns the index value of the maximum sort torch.argmin(input, dim=None, keepdim=False) #Returns the minimum sorted index value torch.cumprod(input, dim, out=None) #y_i=x_1 * x_2 * x_3 *...* x_i torch.cumsum(input, dim, out=None) #y_i=x_1 + x_2 + ... + x_i torch.dist(input, out, p=2) #Returns the p-type distance between input and out torch.mean() #Return average torch.sum() #Return sum torch.median(input) #Return intermediate value torch.mode(input) #Returns a numeric value torch.unique(input, sorted=False) #Return the unique tensor of 1-D, and return each value once >>> output = torch.unique(torch.tensor([1, 3, 2, 3], dtype=torch.long)) >>> output tensor([ 2, 3, 1]) torch.std( #Return standard deviation) torch.var() #Return variance torch.norm(input, p=2) #Returns the normal form of p-norm torch.prod(input, dim, keepdim=False) #Returns the product of each row of the specified dimension
Comparison operation
torch.eq(input, other, out=None) #Perform equation operation according to members, and return 1 if the same
torch.equal(tensor1, tensor2) #true if tensor1 and tensor2 have the same size and elements
>>> torch.eq(torch.tensor([[1, 2], [3, 4]]), torch.tensor([[1, 1], [4, 4]]))
tensor([[ 1, 0],
[ 0, 1]], dtype=torch.uint8)
>>> torch.eq(torch.tensor([[1, 2], [3, 4]]), torch.tensor([[1, 1], [4, 4]]))
tensor([[ 1, 0],
[ 0, 1]], dtype=torch.uint8)
torch.ge(input, other, out=None) # input>= other
torch.gt(input, other, out=None) # input>other
torch.le(input, other, out=None) # input=<other
torch.lt(input, other, out=None) # input<other
torch.ne(input, other, out=None) # input != other is not equal to
torch.max() # Returns the maximum value
torch.min() # Returns the minimum value
torch.isnan(tensor) #Judge whether it is' nan '
torch.sort(input, dim=None, descending=False, out=None) #Sort the target input
torch.topk(input, k, dim=None, largest=True, sorted=True, out=None) #Returns the maximum k values and their index values along the specified dimension
torch.kthvalue(input, k, dim=None, deepdim=False, out=None) #Returns the minimum k values and their index values along the specified dimension
Spectrum operation
torch.fft(input, signal_ndim, normalized=False) torch.ifft(input, signal_ndim, normalized=False) torch.rfft(input, signal_ndim, normalized=False, onesided=True) torch.irfft(input, signal_ndim, normalized=False, onesided=True) torch.stft(signa, frame_length, hop, ...)
Other operations
torch.cross(input, other, dim=-1, out=None) #Cross product torch.dot(tensor1, tensor2) #Returns the dot product of tensor1 and tensor2 torch.mm(mat1, mat2, out=None) #Returns the product of matrices mat1 and mat2 torch.eig(a, eigenvectors=False, out=None) #Returns the eigenvalue / eigenvector of matrix a torch.det(A) #Returns the determinant of matrix A torch.trace(input) #Returns the trace of a 2-d matrix (summation of diagonal elements) torch.diag(input, diagonal=0, out=None) # torch.histc(input, bins=100, min=0, max=0, out=None) #Calculate the histogram of input torch.tril(input, diagonal=0, out=None) #Returns the lower triangular matrix of the matrix. The others are 0 torch.triu(input, diagonal=0, out=None) #Returns the upper triangular matrix of the matrix. The others are 0
Tips
Get python number
After Python 0.4, python number is obtained uniformly item() method:
>>> a = torch.Tensor([1,2,3]) >>> a[0] #Direct index retrieval returns tensor data tensor(1.) >>> a[0].item() #Get python number 1
tensor settings
Judgment:
torch.is_tensor() #If it is the tensor type of pytorch, return true torch.is_storage() # If it is the storage type of pytorch, return true
Here's another tip. If you need to judge whether the tensor is empty, you can do the following
>>> a=torch.Tensor() >>> len(a) 0 >>> len(a) is 0 True
Setting: through some built-in functions, you can set the precision, type and print parameters of tensor
torch.set_default_dtype(d) #Yes, torch Tensor() sets the default floating point type torch.set_default_tensor_type() # Ibid., for torch Tensor() sets the default tensor type >>> torch.tensor([1.2, 3]).dtype # initial default for floating point is torch.float32 torch.float32 >>> torch.set_default_dtype(torch.float64) >>> torch.tensor([1.2, 3]).dtype # a new floating point tensor torch.float64 >>> torch.set_default_tensor_type(torch.DoubleTensor) >>> torch.tensor([1.2, 3]).dtype # a new floating point tensor torch.float64 torch.get_default_dtype() #Get the current default floating-point type torch dtype torch.set_printoptions(precision=None, threshold=None, edgeitems=None, linewidth=None, profile=None)#) ## Set printing parameters for printing